特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【#1】数学の学習のスタート!〜数学との出会いを大…

本連載では、授業づくりのポイントや教科書の使い方などについてお伝えしたいと考えています。毎日忙しくて教材研究する時間があまり取れない…とお悩みの先生、ちょっと立ち止まって明日からの授業を一緒に考えてみませんか。(佐藤寿仁)
数学の学習のスタート!〜数学との出会いを大切にする〜
令和5年度、そして、新学期が始まりました。中学校では、小学校を卒業した新1年生が入学します。算数から数学に変わることで学習に期待をよせている生徒もいるでしょう。しかし、「数学になると難しくなるのかな…」と少し不安な生徒もいるかもしれません。
新年度、新学期のスタート。数学の授業づくりでどのようなことを大切にしていますか?
◎新1年生への数学の「授業開き」、どんな工夫がありますか?
新1年生の中には「数学」という名称に緊張してしまう生徒もいるでしょう。「授業開き」を大切にしたいですね。中学校の先生にお話を聞くと、「授業開き」は最初の数学の1時間で「授業の受け方」「ノートの取り方」「期末試験までの見通し」「評価(成績)の付け方」などのガイダンスを行う場合が多いようです。もちろんそれらを伝えることは大切です。ただ、最初の1時間だけに拘らず、数時間をかけて「学び方」について一緒に考える「授業開き」があってもよいと考えています。
東京書籍の1年生の教科書では、「0章 算数から数学へ」という単元から始まります。これを数学の授業開きとして取り上げることにします。
算数で学んだ九九、それをまとめた九九表が示されています。小学校2年生のときには、同数累加となる加法に着目し、2の段から乗法について見いだし、九九としてまとめてきました。九九を自らつくってきたのですね。そして、加減乗除の計算を進める過程で大きい数、小数や分数などに数の世界を積極的に拡げ、加減乗除の計算をどんな数でもできることを確認してきました。中学校ではこれらを踏まえた上で、九九表を見せて、「どんなきまりがあるかな?」と問いかけてほしいです。探究のスタートです!
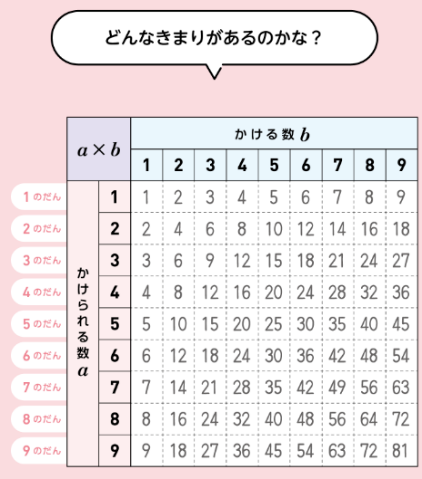
生徒は、九九表を観察することで、様々なところに着目をして、きまりを見いだすことでしょう。
「横にみたら、倍数が並んでいます!」
「あっ、縦でも同じようなことがいえるよ!」
「増え方にもきまりがあると思います!」
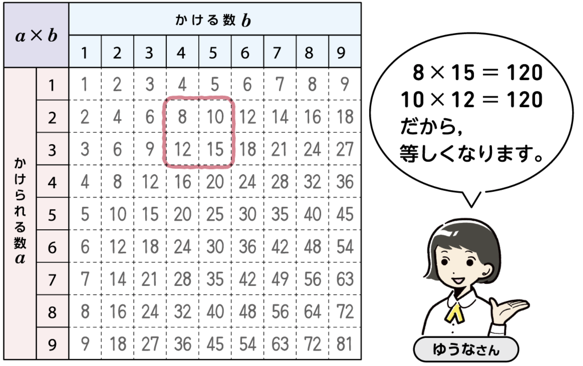
などと話し合ったり、それを発表したりする場面を設定したいですね。その際、教科書の「ゆうなさんの吹き出し」を積極的に利用することも考えられます。
「ゆうなさんの吹き出し」にある気づきから、どんなきまりがあるのかをみんなで予想すること、また、「ゆうなさんの見つけたきまり」を成り立つと予想される事柄として確認してもよいですね。
さあ、ここから、探究が加速します!「ゆうなさんの見つけたきまり」は、ほかのところを囲んでも成り立つかどうかを検証・検討する活動のスタートです。正方形で囲んだ数を自分で決めて、その計算結果を交流する場面の設定です。
九九表を観察し、そこにどんなきまりがあるのかについて、学級で話し合いました。その際に、対話や協働で「きまりを発見する」という問題解決をします。九九表で「縦2ます横2ますの正方形で囲むと、斜めの数どうしの積が等しくなる」ことについて、どこを囲んでも成り立つことを確認した生徒に、あなたなら次にどのような発問をしますか?生徒には、問題解決することだけでなく、問い(問題)を発見することも大切にしてほしいです。ここでは、発見したきまりについて、「次にどんなことを考えてみたいか」と問うことで、「きまりがいつでも成り立つ理由を考えてみたい!」という問いが生まれます。生徒は帰納的な推論を始めるかもしれません。こうした問いをもとにさらに考察を進め、数の構造や構成などに着目するようになり、素因数分解の学習につながるのです。
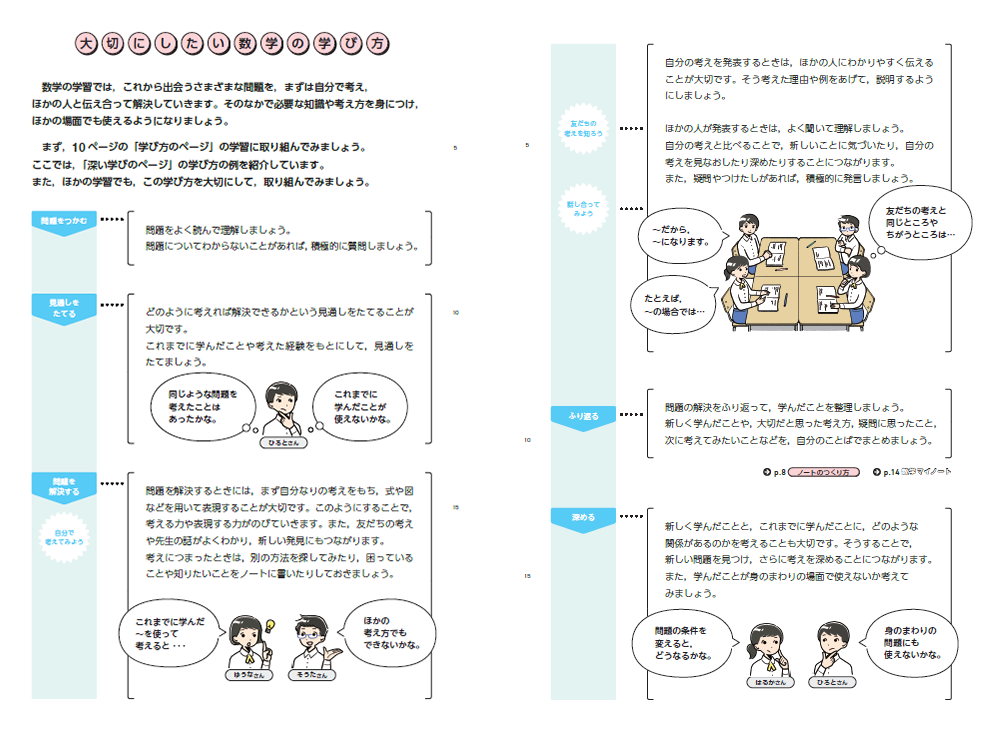
さて、本時の問題解決を振り返るだけでなく、今後の授業での「学習の進め方」を学級で確認する場面を設定してみるのはいかがでしょうか。このとき、教科書にある「大切にしたい数学の学び方」を活用することをお勧めします。授業の受け方について、ガイダンス的に先生が説明することもよいですが、この0章での学びを通して、中学校においても数学の授業では、問題解決を目標に「自分で考え、さらに話し合いなどの対話を通して、学級で検討し問題解決する」など、よりよい学び方について一緒に考えてみましょう。
◎中学校数学のスタート、どうして素因数分解の学習からなのですか?
「0章 算数から数学へ」では、「自然数を素数の積として表すこと、」すなわち「素因数分解」が学習内容として含まれています。このことは、算数で考察し続けてきた整数の性質の理解をさらに進めることになります。この単元では単に「素因数分解ができればよい」ということではありません。整数について、素数を用いた積で捉え、その表し方が1通りに決まることを生徒が見いだせるように工夫することが大切です。
1年生の生徒は、6年間の算数の学びを通して、偶数、奇数、約数、倍数、最大公約数、最小公倍数などの整数の性質を学んできました。素因数分解を学習することで、それらの整数の性質を捉え直すとともに、整数の性質の理解をさらに一歩進めるのです。算数から数学へ教科名が変わることで学習内容が難しくなるということでなく、これまでの算数を大切にしながら、その世界を自分たちでさらに切り拓いていくことの大切さも、授業を通して確認していきましょう。
さあ、次の単元では、いよいよ数の世界を拡げる負の数への拡張ですね。
負の数へ拡張するための生徒の問いは、どんな「問い」でしょうか?
【佐藤寿仁先生 略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。
その他のコンテンツ
