特集記事（小中学校）

本連載では、授業づくりのポイントや教科書の使い方などについてお伝えしたいと考えています。毎日忙しくて教材研究する時間があまり取れない…とお悩みの先生、ちょっと立ち止まって明日からの授業を一緒に考えてみませんか。（佐藤寿仁）

数学の学習のスタート！〜単元の導入編：第1章「多項式」〜

　前回は新1年生の授業開きについて話題としました。今回は3年生です。
　授業開きで、3年生に「高校受験に向けて…」と声をかけることだけが中心となってはいませんか。もちろん、進路選択ですのでとても大切です。でも、数学の主体的な学びに弾みをつけることができるような導入場面を設定することも大切だと考えています。
　第1章「多項式」導入場面を例に1年間の学習のスタート、単元の導入場面を考えてみましょう。

◎中学3年生第1章「多項式」の導入場面、どんな工夫がありますか？

　みなさんは単元の導入場面で、どのようなことを大切にして授業されていますか？
　第1章「多項式」において、「多項式の計算ができる」「因数分解ができる」といった知識・技能を早く指導するために、教科書p9〜11の導入をサッと終わらせてしまっている、ということはありませんか。単元の導入場面で大切にしたいことは、次時への“問い”とこの単元で解決してみたい“問い”を生徒が発見することです。教科書を活用して、単元の“問い”の発生を考えてみましょう。

　まず、教科書p9を開き「数と式」におけるこれまでの学習内容について生徒と振り返ってみましょう。数を負の数に拡張して四則計算の可能性を追究したこと、文字式について計算したこと、文字式を用いて数の性質を発見し、それが一般的に成り立つことを説明したことなど生徒とやりとりして思い出してみましょう。場合によっては、1、2年生の教科書を実際に見たり、デジタル教科書を電子黒板に写したりするのもよいですね。　

　単に計算だけでなく、数の性質について帰納的、演繹的に考えるなど数学的な考え方を学んできたことも確認したいですね。その後、ドミノ倒しの写真をみて、「一番早くゴールするのはどれ？」と問い、考察が始まります。

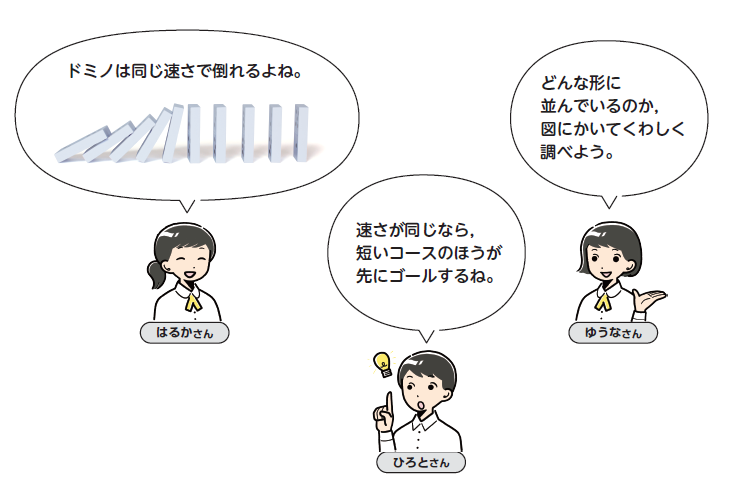
　「やってみないとわからないよ！」と話す生徒もいます。そのとき、「数学で考えなさい！」ではなく、上の3人の会話を読み、見通しを持つとよいです。「ゆうなさんの吹き出し」を見て、「このドミノ倒しを図に表すと、どんな図がかけるかな？」などと問い、ドミノの並びを弧（半円）として捉えるといった数学化する場面を設定するとよいです。事象を単純化して、それを数学的に表現することも、これまで大切にしてきた数学的な見方です。

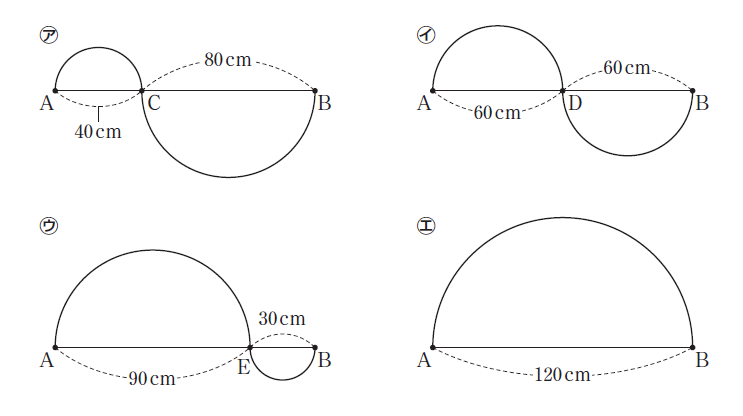
　ドミノの並びを弧として考えることで、図のア〜エのように表し、弧の長さの和を求めます。このとき教科書では、「どんなことがわかるでしょうか」と問うていますね。この場合、全て60\(\pi\)cmになりますが、「…ということは何がいえるの？」と問い、計算結果からどのコースも道のりが等しいことについて説明する場面を設定することも大切です。

　また、このとき60\(\pi\)cmという計算した結果だけでなく、その求めた式についても確認し、板書や生徒のノートに残しておきましょう。次の授業への伏線（フラグ）となる仕掛けになりますよ！

　数学的に説明ができたものの、何かモヤモヤする生徒もいるでしよう。「結果は60\(\pi\)cmになるけど…」のように、本当にこのドミノ倒しが同時に終わるかどうか戸惑うことがあるのです。ここで、Dマークコンテンツを利用してみましょう。動画を見た後に、道のりが60\(\pi\)cm、ドミノが倒れる速さも同じとみたことで、予想が成り立つことを、実感を伴って理解することができます。なお、この動画を使用するタイミングには、授業によって様々考えられるでしょう。

　さて、ここまでくるともう授業は終わったように思えるかもしれません。しかし、ここからが本番ですよ！いよいよ、ここから学級のみんなで“問い”の発見です！

　ア〜エの図を振り返ります。それらの図において、「変わるもの」と「変わらない」ものは何か、生徒に問うてみましょう。すると、下のことについて見いだしてくれるでしょう。

　ここで、事象の振り返りです。ドミノ倒しという事象について数学的に考察をしてきたわけですが、ア〜エは、この点PがC、D、E、そしてBの位置にあるとすれば、点Pを連続的な動きをとる点として解釈できることを学級のみんなで対話を通して確認・共有することが大切です。さらに、「次にどんなことを考えてみたいか、どんなことを明らかにしてみたいか」と問うことで、生徒は話し合い、今後考えてみたいことについて、具体的にあげてくれるのではないでしょうか。これが生徒にとって自分事となる“問い”になるのです。

　こうして、本時では、ドミノ倒しについて数学的に捉え、「長さ120cmの線分AB上に点Pをおき、線分AP、PBを直径とする半円において、その弧の長さの和は変わらない」ことを問題として整理し、さらに、次時では文字式を用いて、そのことが点Pの位置に関係なく等しくなることやABの長さを変えても同じ関係が成り立つことを説明する時間となるのです。

◎本時を通して、生徒が持つ“単元の問い”とはどのような問いでしょうか？

　導入での最後の場面で次時の問題を発見した生徒達に、さらに問うてみませんか。
「この単元では、どんなことを考えてみたい？どのようなことをはっきりさせてみたい？」など。
　3年間の集大成となることで、これまでの学びを思い起こしながら、例えば、下のようなことを挙げてくれるのではないでしょうか。

• → 2年生のときと同じように、文字式を使って数の性質を発見したい！
• → 使う文字式が1、2年のときの変わるのかな？どんなふうにかわるのかな？難しくなるの？
• → 1、2年生よりも文字式が難しくなったとしても、変わらないことはあるのかな？

　生徒とやりとりをしながら、この単元でどのようなことを学ぶかについて、学級のみんなで考えるとよいでしょう。文字式の学習であることは分かると思いますが、それがどのように変わるのか、同じようにして考えることはあるのかといった計算方法や式表現について、また、文字式を用いて論理的に考え、それを表現することなどを話題とすることができればよいですね。
　生徒が見いだした“単元の問い”については記録し、単元の終末場面でその答えについて学級で話し合い、単元の学びを振り返るとよいでしょう。

　中学校最後の1年間。数学でのどのような学びが待っているかのワクワク感と、数学を学ぶことの意義を大切にしながら、生徒が数学的に考えることが楽しい授業をつくりましょう！

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。