特集記事（小中学校）

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第8弾になります。

　令和4年度実施の全国学力・学習状況調査 中学校数学大問7(2)を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：箱ひげ図を用いて問題解決すること

※全国学力・学習状況調査より

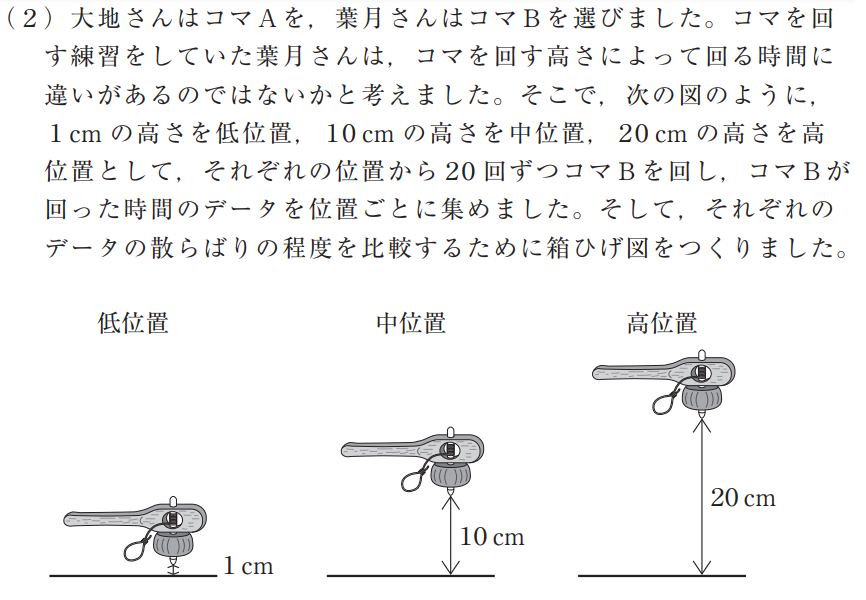
　大問7(2)は、箱ひげ図を用いてデータの分布の特徴について読み取ることができるかどうかをみる問題です。設問(1)では、コマAが回った時間とコマBが回った時間のヒストグラムから、分布の様子をみてどちらのコマがより長い時間回りそうかを判断し、コマを選択しました。この設問では、コマを選択した理由について数学的に説明することが求められています。設問(2)は、コマAを選択した大地さんが、コマがより長い時間回すために、回す位置に注目し、高位置・中位置・低位置という3つの位置でどれがふさわしいか考察します。それぞれの位置において実験してデータを収集し、それを箱ひげ図に整理して考察する文脈です。

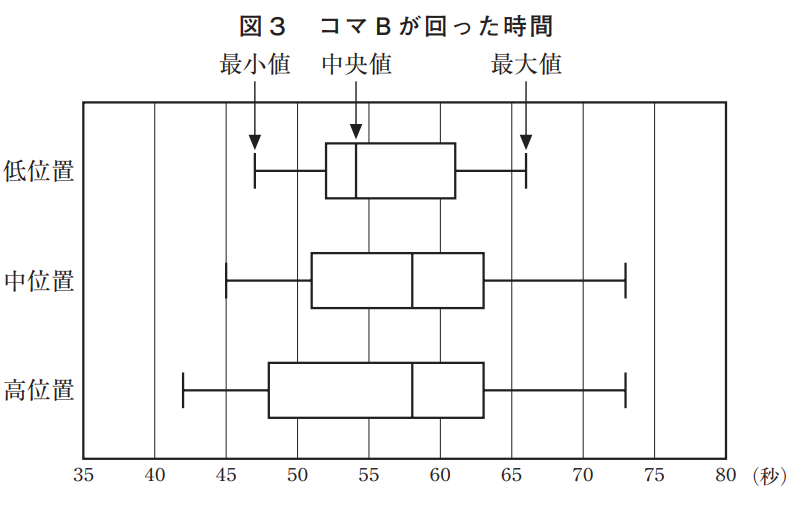
この設問の評価の観点は、「知識・技能」で、四分位範囲や箱ひげ図の必要性と意味を理解しているかどうかをみるものです。3つの箱ひげ図における四分位範囲（問題では「箱が示す区間」と表記）に着目して、そこに含まれるデータの個数と散らばりの程度について解答します。四分位範囲は、第3四分位数から第1四分位数を引いた値で、その間にはデータの約半数があることを意味し、データの散らばりの度合いを表す指標として用いられます。

正答は選択肢アであり、箱の横の長さについて、高位置よりも中位置のほうが短いことから散らばりの程度を判断することができます。選択肢ウ、エは、箱の横の長さが長いことからデータがより多く含まれるといった誤った捉えを想定しているものす。箱の横の長さが長い・短いといったことと、箱に含まれるデータの個数の大小について同じように考えてしまうという回答を選択することが予想されます。

この問題の場合には、高位置・中位置・低位置のそれぞれのデータは20個で等しく、箱が示す区間にはデータが10個含まれていることを指摘できるよう、学習指導が必要です。

POINT②：箱ひげ図の必要性やその意味を理解すること

　中学校学習指導要領（平成29年告示）では、箱ひげ図の指導内容について高等学校数学から第2学年に移行措置されました。今回、この箱ひげ図の内容について全国学力・学習状況調査中学校数学での初めての出題となりました。 中学校学習指導要領（平成29年告示）解説数学編では、「箱ひげ図の必要性と意味の理解」、「箱ひげ図を用いて批判的に考察し判断すること」を育成すべき資質・能力として設定しています。

本設問では、知識・技能を評価しようとしていますが、箱ひげ図について、第1四分位数、中央値、第3四分位数、範囲といった用語について知ることやそれらを求めることができるようになるといったことだけでなく、箱ひげ図がデータの散らばりの程度を表すことなどについて、生徒が統計的に問題解決することを通して実感を伴って理解することが必要です。さらに、箱ひげ図は複数のデータの分布を比較する際の統計的表現として有効であり、第1学年で学んだヒストグラムや度数折れ線を振り返りながら、箱ひげ図のよさについて確認することも大切です。

POINT③：教科書の構成を生かして授業を構想すること

　取り上げた大問7のように、統計的に問題解決する際に、箱ひげ図を用いてデータの分布の特徴を調べることは、第2学年のデータの活用にとって大切な学習です。教科書において、そのような場面が設定されており、生徒の統計的な問題解決のある授業を実現することができます。具体的な場面を紹介します。

　教科書p.184、185では、本章で考察してきたスナック菓子、茶系飲料、炭酸飲料、チョコレートそれぞれの販売数の傾向について箱ひげ図を用いて考察し判断するという活動が設定されています。

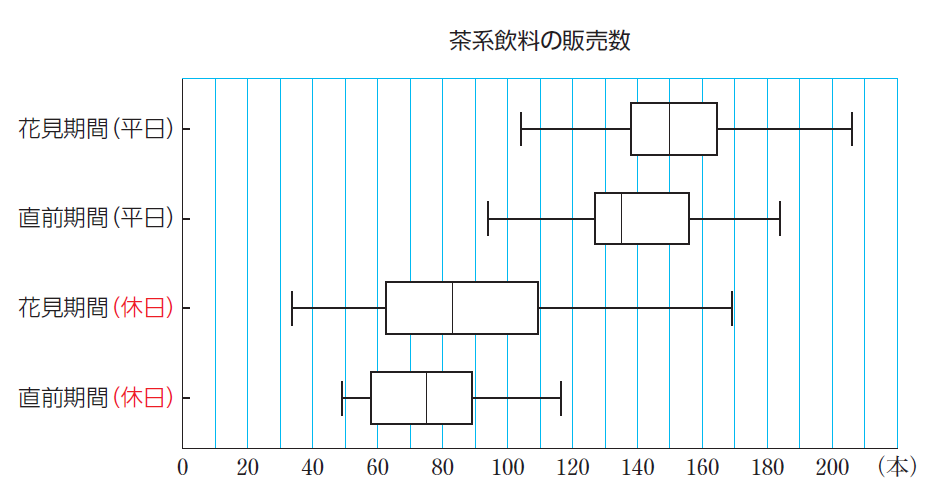
　例えば、茶系飲料の販売数の4つある箱ひげ図を比較してみると、「花見期間（平日）」では最大値及び中央値（第２四分位数）が大きく、箱が右側に位置していることがわかります。さらに、四分位範囲が小さいことを読み取ることができ、販売数が安定して多いことがわかります。授業では、このようなことについて話し合う場面を設定し、箱ひげ図においてデータの散らばりの度合いを調べることが大切です。

また、「花見期間（休日）」は、範囲が大きく、四分位範囲も大きいことがわかります。箱ひげ図から読み取ったことをもとに、「花見期間（平日）」には茶系飲料がよく売れていたこと、「花見期間（休日）」には売れる日もあるがそうでない日もあることの背景について考えることも大切です。

さらに、「花見期間（平日）」と「直前期間（平日）」の箱ひげ図のかたちが似ていることから、分布の特徴についてさらに調べたいといったことが生徒からでてくることが考えられます。

教科書p.183について振り返って考えたり、また、教科書p.190〜192に掲載されている実際のデータをもとにして、コンピュータ等を利用してヒストグラムをつくり、それをもとに考察したりする場面を設定することもよいです。