特集記事

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第7弾になります。

　令和4年度実施の全国学力・学習状況調査 中学校数学大問9(2)を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：成り立つと予想した事柄について、論理的に考察すること

※全国学力・学習状況調査より

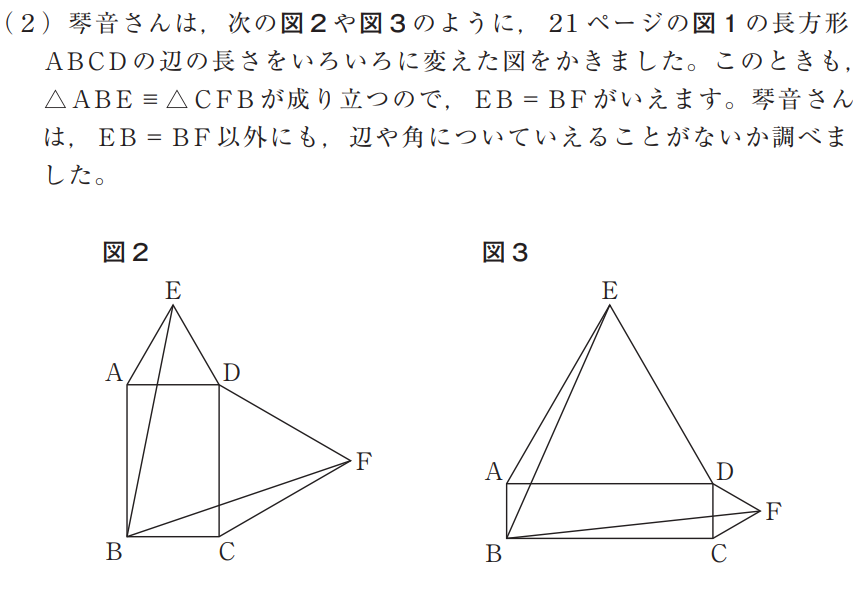
　大問9(2)は、予想した事柄が成り立つことを、筋道を立てて考え、事柄が成り立つ理由を説明するこができるかどうかをみる問題です。設問(1)から長方形ABCDの辺の長さをいろいろに変えた図においても線分EBと線分BFの長さが等しくなります。このことを受けて(2)では、さらに考察を進めるという文脈において、新たな問として予想した「\(\angle\)EBFの大きさが60°になる」ことが成り立つ理由を説明するというものです。

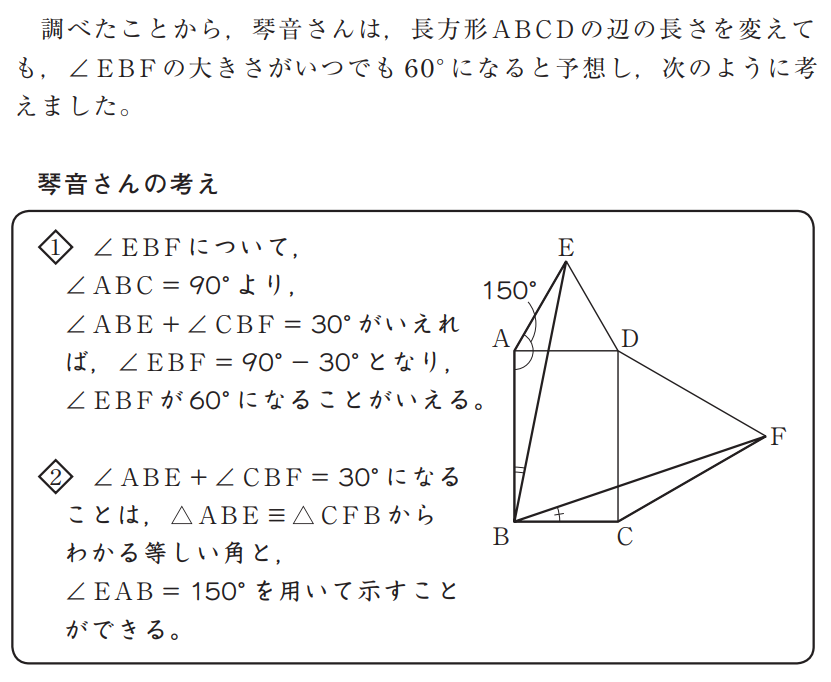
実際には、\(\angle\)EBFの大きさが60°になることを示すために、\(\angle\)ABEと\(\angle\)CBFの和が30°を示すことができればよいといった問題中の「琴音さんの考え」の見通しや構想をもとに、焦点化された問題である「\(\angle\)ABEと\(\angle\)CBFの和が30°になる」が成り立つことの理由を記述します。証明の一部の記述です。その際には、「琴音さんの考え」の2つ目に書かれていることについて、生徒が解釈することが必要です。

具体的には、\(\triangle\)ABEと\(\triangle\)CFBが合同であることから、図形間の関係における構成要素どうしの相等関係、三角形の3つの角における関係のような2つのことを捉え、下のように表現することが求められます。

\(\angle\)AEB\(=\angle\)CBF･･･①、\(\angle\)ABE\(+\angle\)AEB\(=\)30°･･･②

　①、②の関係より、「\(\angle\)ABE\(+\angle\)CBF\(=\)30°」を導き、「\(\angle\)ABEと\(\angle\)CBFの和が30°になる」ことについて説明します。これらの数学的な説明は、多くの生徒にとって簡単に進められるものではないと予想されますが、実際の授業では、証明の書き方に拘ることなく、ある事柄が成り立つことを「根拠と結論」を明らかにする過程を重視し、生徒とのやりとりや話し合いの場面を設定するなどして、数学的に考えることを大切にするとよいでしょう。

POINT②：ICTなどを利用し観察や操作、実験を通して、事柄について予想する場面を設定すること

　本問は、「図形の論証を進め、それを数学的に表現すること」を思考・判断・表現の観点で評価することが考えられます。授業では、生徒が証明を考え、それを書くといった活動が山場にはなるのでしょう。学習指導要領では「数学的活動の充実」を求めています。数学における問題発見・解決の過程を重視することを考えると、証明を書くことだけでなく、実際に図を動かしたりしながら、成り立つと予想される事柄を生徒自身で考えることも大切です。

問題では、「長方形ABCDの辺をいろいろに変えて」とあります。実際に図を書いて「\(\angle\)EBFの大きさが60°になる」と生徒が予想する場面を授業に取り入れることが大切です。しかし、図形を動的に表す際に、ノートなどに書くことは大変ですから、コンピュータを利用することが考えられます。1人1台端末を利用し、生徒が図形を観察や操作をすることで、「\(\angle\)EBFの大きさが60°になる」といった事柄の予想をし、自分事の問いとして粘り強く考察することにつながるのです。

POINT③：教科書の構成を生かして授業を構想すること

　取り上げた大問9のように、図形を動的に考え、成り立つと予想される事柄を見いだし、それを論理的に考察すること、また、統合的・発展的に考えることは、第2学年の図形領域にとって大切な学習となります。教科書においても、そのような場面が設定されており、数学的な見方・考え方を働かせた豊かな考察のある授業を実現することができると考えます。このことについて、具体的な場面を紹介します。

　教科書p.152、153の「深い学び」では、1点を共有する2つの正三角形において成り立つ性質を調べる活動が設定されています。「深い学び」では数学的活動を重視した構成になっていますので、授業づくりの際に、その考察の過程を構想するのにも参考になります。

最初は、正三角形の頂点であるA、C、Bが一直線上にある場合について考え、線分AEと線分DBが等しいことを証明します。その後、教科書p.153の❸にあるように、正三角形CBEを点Cを中心に回転させても、AE\(=\)DBが成り立つかどうかの問いへ移ります。統合的・発展的に考える場面です。教科書には図が掲載されていますが、図形を回転移動させるという操作ですので、生徒が実際に動かしてみるといった活動が大切です。

そこで、教科書p.153の❸に設定されているDマークを利用してみてはいかがでしょうか。このDマークは、インターネット上のコンテンツが使用可能であることを示しています（※教科書p.4を参照）。このコンテンツを、1人1台端末で利用することにより、生徒は操作活動に取り組むことができます。そして、正三角形CBEを点Cを中心にして回転させても、AE\(=\)DBが成り立つのではないかと考えなど、統合的・発展的に考察することにつながるのです。

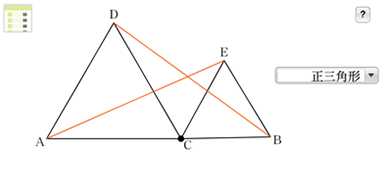
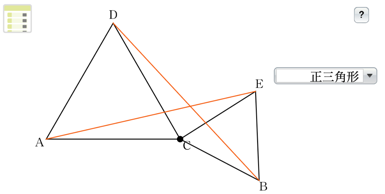
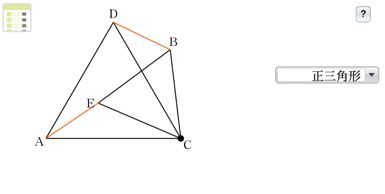
　なお、このコンテンツでは、考察の対象としている図形を正三角形から他の図形に変えることもできます。図形を変えても、AE\(=\)DBが成り立つことが予想することができます。そして、自分たちが書いた証明とコンテンツで見ている図と見比べることで、AE\(=\)DBが成り立つことの前提が、図形の具体の形にあるのではなく、「CA\(=\)CD、CB\(=\)CEであればよい」といった本質的な条件（前提）にも気づき、この事象について統合的に考えることができるようになるのではないでしょうか。