筑波大学附属駒場中・高等学校
須藤 雄生 先生
新課程が施行されて初めての大学入学共通テストが行われました。事前に大学入試センターが公表した問題作成方針によると,昨年度まで見られた「高等学校における『主体的・対話的で深い学び』の実現に向けた授業改善のメッセージ性」という文言が消え,「深い理解を伴った知識の質を問う問題や,知識・技能を活⽤し思考⼒・判断⼒・表現⼒等を発揮して解くことが求められる問題を重視する」という表現になりました。
新テスト開始当初の,大きく振りかぶって「この問題に対応できるような授業を高校でやっていますか!」というボールを投げ込んでくるイメージこそ薄れましたが,むしろ非本質的な「対策のいたちごっこ」になるのを嫌った変化ともみられます。よりよい高大接続教育の実現のために毎年魂のこもった問題を世に送り出している作問委員の先生方に,あらためてここで敬意を表します。
本稿では,高校現場の一教員として,今年度の「数学Ⅰ,数学A」の問題を振り返り,今後の教材開発や授業に生かしていけそうなことを検討していきたいと思います。
■ 第1問〔1〕数と式
「平方根の近似を式変形で求める」という一連のストーリーがあった昨年度と比べると,やや“単発問題の寄せ集め”感の強い構成になっているように感じます。
因数分解に手間取りそうなところで \(a\) の係数が1であることが与えられていたり(解答欄[オ]),有理化の符号を間違えやすいところで符号が与えられていたり(解答欄[キ][ク]),マーク形式に起因する過剰なヒントが出てしまっているのは何となくもったいない気もしましたが,久しぶりに姿の見られた必要条件,十分条件を答える設問で,こういった方程式の解の吟味で最もありがちな「十分条件であるが必要条件ではない」を調べる形になっていたのは素直で良い設定だと思いました。
■ 第1問〔2〕三角比
用いる道具が,誘導に従うと「三角比の定義」→「正弦定理」→「余弦定理」という,多くの受験者にとって修得した順序どおりになっているところには工夫を感じました。一方,「正弦定理」の名前が出てくる誘導のくだりでわざわざ図にない外接円が登場し,それを経由して \(\text{PA}\sin\alpha=\text{PB}\sin\beta\) という三角比の定義から自然に導かれる等式に至っているのは個人的には不可解で,これが結果として「公式丸暗記勢をかわす誘導」になるのか,あるいは「公式丸暗記勢を助長する誘導」になるのか,懸念しているところです。
また,受験者にとっては恐らく試験時間内では検証しないであろう最後の1行「\(\text{QA}=\sqrt{7}\) であることがわかる」をあえて問題文に残していることの意味も,授業で教材としてこの問題を取り上げるのであれば追究してみたいところです。
■ 第2問〔1〕2次関数
太郎と花子が公園の噴水から放物線の問題を見いだすという,状況だけ考えると多分に無理のある設定の会話文ですが,「高さと横幅だけを考えて放物線の位置を制御する」という,数学の内容としては決して奇をてらったものではありません。
むしろ「これは放物線ではなく噴水なのだから,式にこだわらず高ささえ求めればよい」という思わぬ副次的効果を生んでいるようにも感じました。具体的には,左右の噴水の高さが1.8メートルであり,頂点の位置が \(y\) 軸からそれぞれ左右に1メートルであることが分かった時点で,中央の大きい噴水の高さは図のように比だけを使って
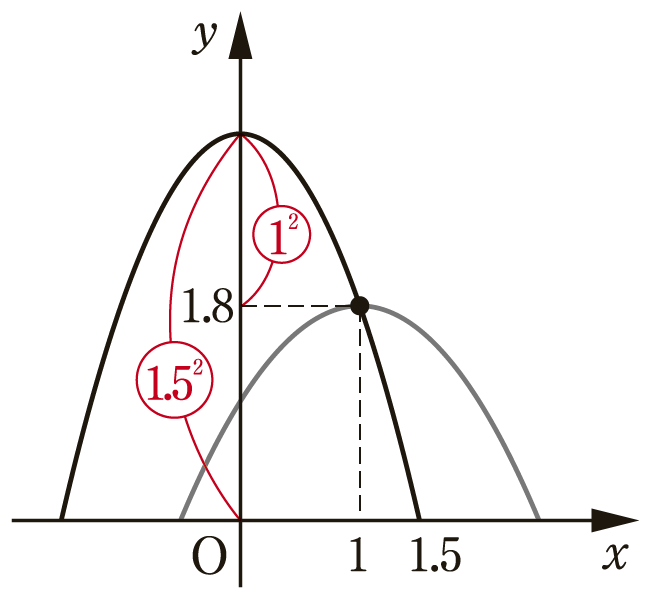
\(1.8 \times \frac{1.5^2}{1.5^2-1^2} =1.8\times 1.8=3.24\)
であることが求められ,途中から放物線の式はほとんど必要がなくなります。この観点で,「大きな噴水の高さは,小さな噴水の高さのおよそ何倍か」が問われているのもいたって自然です。
この教材をもし私が授業で扱うならば,決して2次関数の式の形式的処理に傾倒させることなく,「噴水の高さ」という具体的な値に着目して放物線の性質を発見できる教材として扱いたいと思っています。
■ 第2問〔2〕データの分析
与えられた散布図に主張が整合しているかどうかや,2変量の和の分散と共分散の関係を2次式の計算をまじえて示すこと,そして仮説検定の考えなど,新学習指導要領の解説で示された内容には忠実な出題であったと考えられます。
ただ,特に「仮説検定の考え」については,限られた時間でこのような問題の形で出てしまうと,どうしても「やみくもに意志決定を迫る」イメージがつきまとうように,個人的には思えてなりません。問題文中で判断の「方針」が示され,その「方針」に沿って単純に帰無仮説を棄却するかどうか判断する,という部分だけを切り取って「大学入学共通テスト」の問題として出題されることで,「方針」の妥当性を検証したり,ときには戻ってやり直したりといった,学習指導要領解説にも書かれているはずの「統計的探究プロセス」の道からおよそ外れた「とにかく方針の妥当性は考えず,数値だけで妥当かどうか判断して答えなさい」という動きを受験者に要求することになってしまいます。そうやって得られた本問の配点4点は,いったい“何を誰に評価された4点”なのでしょうか。そんなことを考えてしまいました。
■ 第3問 図形の性質
切頂多面体の辺の長さや角の大きさを題材とした設定です。(1)はいわゆるデザルグの定理を下敷きにしたもので,証明はシンプルです。一方(2)以降は,いったん外接球を考えたあと,その切断面としての円の性質(方べきの定理)を考えていく内容になっています。この際,外接球ははじめに出てくるだけで,誘導のままに辺の長さを求め,角の大きさを調べて垂直なのかどうか調べたところで問題は終わっていますが,さて「このなかに任意の辺の長さでも球に内接していれば一般に成り立つ性質はあるのか,それとも単に与えられた辺の長さによる特殊性から生まれる性質なのか」という謎は残ります。
授業でこの題材を扱うならば,この先にどのような発展が待っているかを扱うのも面白そうだと感じています。(もっとも,実際にやってみたら「この辺の長さの設定が特殊でした」で終わってしまう可能性もあるわけですが。)
■ 第4問 場合の数と確率
ここ何年か場合の数に比較的寄せた出題になっていたなかで,場合の数が全く出てこない確率の問題でした。初めに条件付き確率の形でそれぞれの事象の確率が提示されるのはおそらく多くの受験者にとって珍しく,しかも(1)を誤ってしまうとそのあとの期待値計算にすべて影響するため,大問まるごと点数がないという悲惨な状況を生み出しかねない怖さは感じます。
蛇足ですが,このように「条件付き確率だけが分かる状況」というのはありうるのか,私なりに考えてみたところ,「主催者がそれぞれの箱に入れたくじの本数が非公開であるため,参加者の結果を相対度数で表したデータから確率を推測することしかできない状況」が,比較的この問題の状況に近いのではないかという結論になりました。そう考えるとさほど不自然な設定ではないようにも見えます。
以上,今年もご無礼を顧みず個人の意見を述べています。拙い分析や背景知識の抜けなどありましたらご指摘いただき,日々の数学の授業を通して生徒に何を経験させたいか,という議論につなげていければ幸いです。
※「数学Ⅱ,数学B,数学C」の振り返りと分析については,2月6日に公開予定です。
参考資料(外部サイトにリンクします)
令和6年度 大学入学者選抜に係る大学入学共通テスト問題作成方針(大学入試センター発表)
令和7年度 大学入学者選抜に係る大学入学共通テスト問題作成方針(大学入試センター発表)
その他のコンテンツ
