特集記事（高校）

茨城県立竜ヶ崎第一高等学校・附属中学校
小林 徹也 先生

「あと5分」の発問例：「視点を変えて整理する」場合

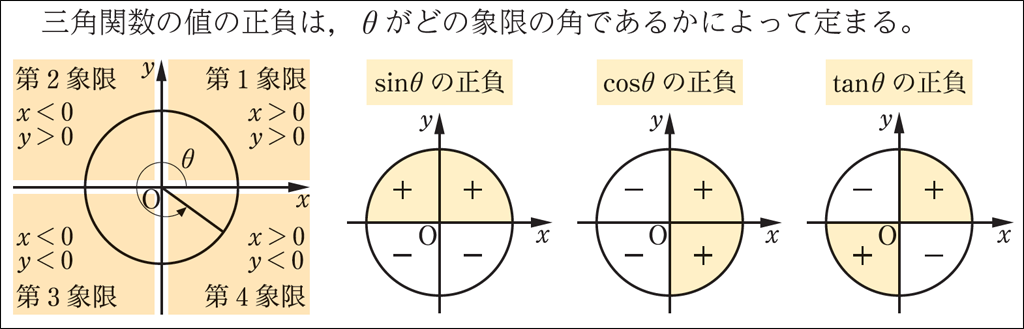
　ここでは，4つの座標平面のうち，最も左の図においては「第\(n\)象限（\(n=1,2,3,4\)）」について，それぞれの象限における\(x\)や\(y\)の正負を確認し，また，「第4象限の角」も図示している。さらに，残りの3つの図では，「\(\sin\theta\)の正負」，「\(\cos\theta\)の正負」，「\(\tan\theta\)の正負」それぞれにおいて第\(n\)象限（\(n=1,2,3,4\)）における正負を符号\(+-\)を用いて表している。
　そこで，見方を逆にして，第\(n\)象限（\(n=1,2,3,4\)）それぞれにおいて，「\(\sin\theta\)の正負」，「\(\cos\theta\)の正負」，「\(\tan\theta\)の正負」を整理させてみたい。発問は次のようになる。

【発問0】 サイン，コサイン，タンジェントすべてが正の値となる象限はあるだろうか。

発問群による授業展開・生徒の反応

　まず，上のように発問し，1 分程度個別に活動させる。この発問に対し，下記のような図を描き始める生徒がいたら，それを取り上げるとよい。いなければ，ヒントとして教師がその一部を示すとよいだろう。

　その後，つぎの発問群を考えさせたい。上の図がイメージできれば次の問題はやさしい。
【発問1】 タンジェントだけが正となる象限はあるだろうか。

　加えて，次の発問をする。
【発問2】 すべてが負となる象限はあるだろうか。またその理由を考えよう。

　そのような象限がないことは図からわかる。理由として，式\(\tan\theta=\dfrac{\sin\theta}{\cos\theta}\)を利用するアイデアなどが生徒から出るとうれしい。出なければ，ヒントとして与えてよいだろう。
　私は10数年前，全国算数・数学研究大会（日本数学教育学会主催）において，次の図「castダイアグラム」を紹介する発表を拝見した。発表では，𝑥 軸 𝑦 軸を書きながら「プラスになるのは」，CASTと書きながら「cast（キャスト）」と言っておられた。その発表者によるとイギリスで使っているという。この図を生徒に見せ，どういう意味があるのか推測させてもいいだろう。

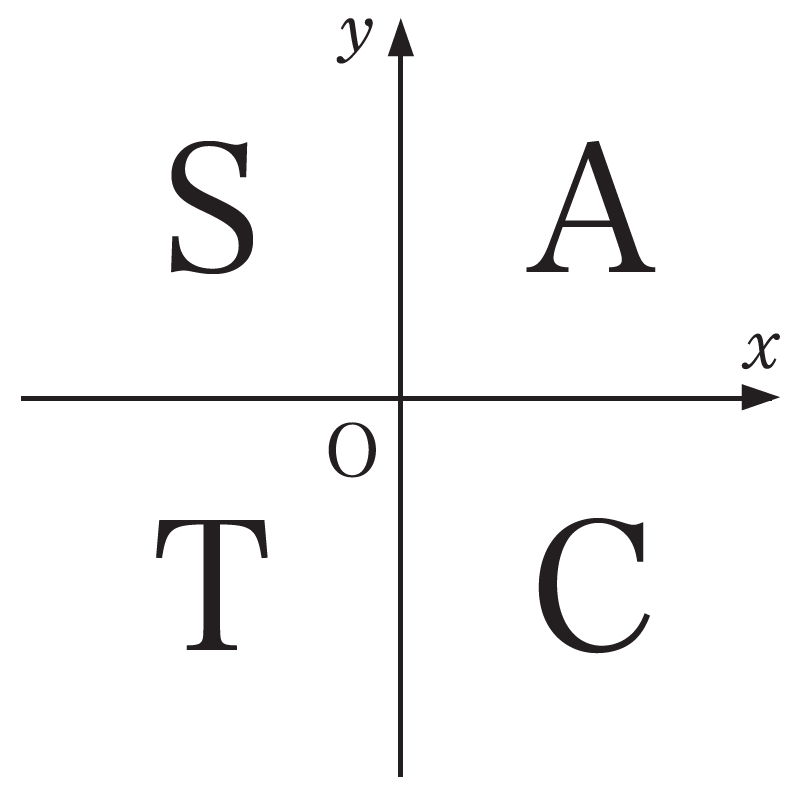
　この図では，

第1 象限　では　\(\text{All}\)（すべて）\(+\)
第2 象限　では　\(\text{Sin}\)のみ\(+\)
第3 象限　では　\(\text{Tan}\)のみ\(+\)
第4 象限　では　\(\text{Cos}\)のみ\(+\)

であること示している。

発問群の活かし方

　発問群により考察の対象の視点を変え，新しい説明を作り出し，さらにそれを用いて考察させる。既習を整理できるだろう。

※後編では，「明確にさせる」場合の発問例についてご紹介します。