Q.
東京書籍の教科書では、5年「四角形と三角形の面積」の学習で、平行四辺形から導入している理由を教えてください。
A.
理由は３つあります。
(1) 等積変形がしやすいこと
(2) 三角形の面積公式が導きやすいこと
(3) 多様な考えが出やすく、既習を活用しやすいこと
（１）平行四辺形は既習の長方形に等積変形しやすいこと
平行四辺形は、図形の分解、移動によって、既習の長方形に変形しやすい図形です。
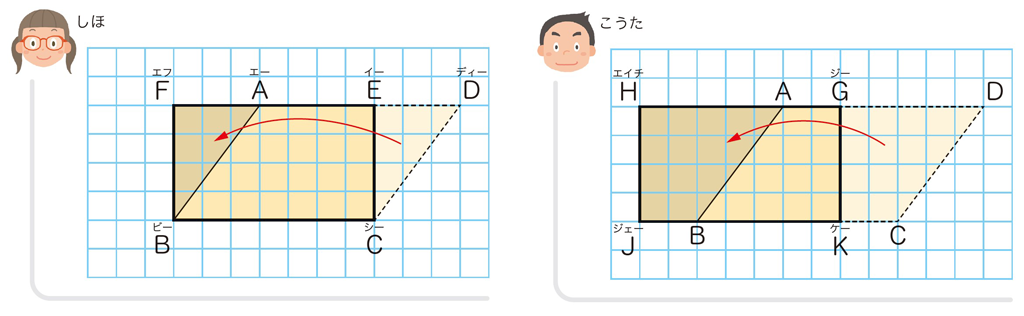
一方、三角形の場合は、まず頂点からの垂線によって２つの直角三角形に分割し、次にそれぞれの直角三角形を２倍して長方形に変形する、という手順を踏むことになります。これらの手続きは、平行四辺形の場合に比べ、操作が煩雑です。
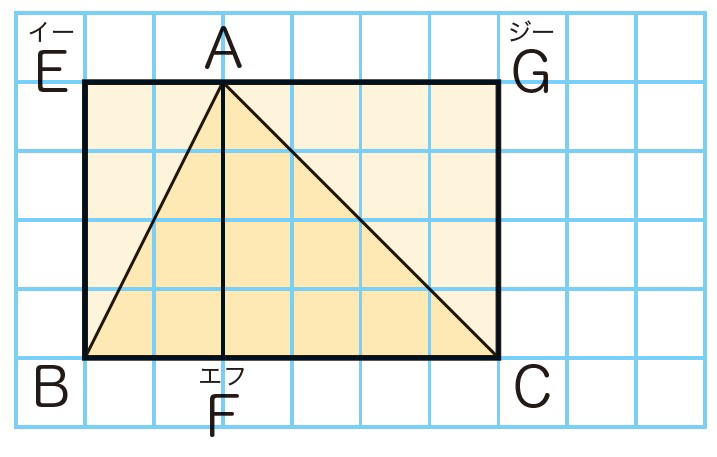
（２）三角形の面積公式が導きやすいこと
三角形を先行させると、平行四辺形の面積公式を導く際も、手続きが煩雑になることが考えられます。
平行四辺形の面積公式を三角形を利用して導く場合、三角形の面積（底辺×高さ÷２）を再度２倍することになります。この「２で割ったものを２倍すること」は低位の子どもにとって混乱の要因にもなりかねません。
一方、平行四辺形を先行させ、三角形の面積公式を平行四辺形を利用して導く場合には、三角形の面積＝平行四辺形の面積÷２と、比較的素直に公式を導くことができます。
（３）多様な考えが出やすく、子ども自身が既習を活用しやすいこと
このことがいちばん大きい理由と考えます。
平行四辺形を先行させる場合、後に三角形や台形などの面積を既習の図形に帰着して考える際、いろいろな選択肢が生まれます。また、その方法も多様です。
一方、三角形を先行させる場合には、常に三角形に戻って考えればよいという考え方が基本になります。確かに基本図形はすべて三角形に分割することができますので、三角形を基本にしていろいろな図形の面積を求められるという長所とも言えます。
しかしながら、この単元で育てたい力を、単に図形の面積の求め方を知ることではなく、既習を用いて多様な考えによって解決する力や、一見異なる多様な考えを１つの式にまとめて表す力と設定すると、必ずしも三角形を基本にする必要はありません。
確かにこの単元では、「帰着させる図形が何であるか」も大切ですが、それ以上に「既習に帰着させる」という考え方そのものに意味がありますね。
平行四辺形と三角形、どちらの求積から導入する場合でも、既習を活かすこと、児童の多様な考えを取り上げること、解決方法の検討を通して１つの式（公式）にまとめられることなど、主体的・対話的で深い学びを進めていくことが大切ですね。
その他のコンテンツ