
岐阜市
はるかです。ここは岐阜県の岐阜市。「和傘」が有名なんだよね。色とりどりで、きれいだなぁ。
この和傘の生産で、岐阜県は全国1位なんだ。2022年には経済産業省の「伝統的工芸品」にも指定されたよ。このあたりは昔から質のいい紙や竹に恵まれて、工芸が盛んだったんだ。中でも和傘は江戸時代の後期に生産が奨励されて、たくさん作られるようになった。最盛期は昭和20年代で、年間1500万本もの傘が作られていたんだって。
へえぇ。そこをピークに、あとは洋傘が多くなっていったのかな。ところで和傘って、骨がまっすぐのままピシっと開くよね。洋傘の方が丸まってる。中にはこんもり、半球に近い形に開く傘もあるし。
さすが、はるかさん! いいところに気づいたね。仕組みが違うんだ。洋傘は、布を外側に出して閉じるよね? でも和傘の和紙は、内側にたたまれる。閉じたとき1本の竹のようにまっすぐに見えるのが美しいとされていて、骨の数も、洋傘よりずっと多いんだよ。

ええと、ふつう傘の骨は6本とか8本のものが多いけど?
和傘は44本や48本のものが多いんだ。つまり、洋傘は6つから8つの二等辺三角形を合わせた形だけど、和傘では、なんと44個の細長い二等辺三角形が合わさっているわけ。
こまやかさが違うね。あれ? そういえば、二等辺三角形を合わせて円に近い形をつくる話って……どこかで聞いたような。円周率に関係があったかな?
そうだね、確かに関係があるよ。昔の数学者は、円に内接する正多角形の角の数をどんどん増やしながら、円周率を計算していったんだ。
やったあ、当たり!
そもそも円周率は、円の直径に対する円周の長さの比率のことだよね。ためしに、正六角形を使って円周率を計算してみる?
了解! よーし、いくよ。まずは、円の内側に接する正六角形のそれぞれの頂点と円の中心を結ぶね。正三角形が、6つ合わさった形になりました。
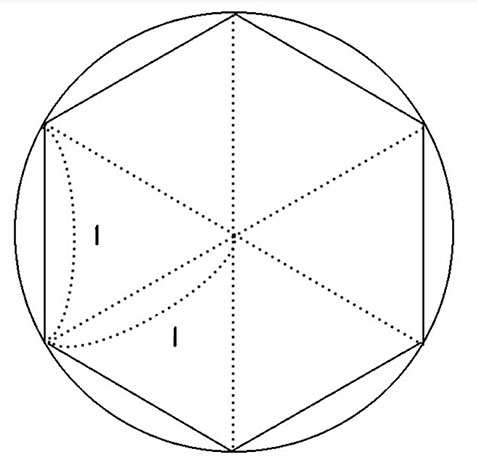
円の半径を1とすると、正三角形の1辺も1。六角形の周は6だから、これを円周と考えて直径2でわると
\(6 \div 2=3\)
つまり、円周率は3、ということになるね。シンプルで、とっても簡単。
はるかさん、カンペキ! じゃあ次に、角の数を倍にしてみたら?
つまり、正十二角形だね。ええと、まずは\(\triangle\mathrm{AOB}\) を考えるよ。
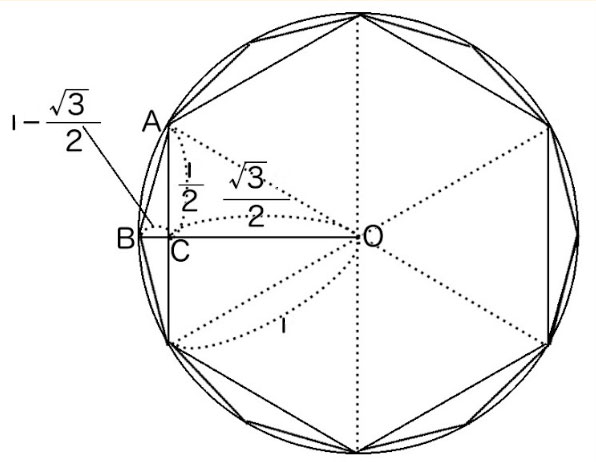
頂点Aから垂線を下ろして、BOとの交点をCとする。\(\angle \mathrm{AOB}=30^{\circ}\) というのが、忘れちゃいけないポイントだね。各辺の長さは、こうなるよ。
\(\mathrm{AO}=\mathrm{BO}=1\) 、\(\mathrm{AC}=\dfrac{1}{2}\) 、\(\mathrm{CO}=\dfrac{\sqrt{3}}{{2}}\) 、\(\mathrm{BC}=1-\dfrac{\sqrt{3}}{2}\)
では、いよいよABの長さを求めてまいります〜。
三角形ABCは直角三角形だから、三平方の定理だね。
\(\mathrm{AB}^2=\mathrm{AC}^2+\mathrm{BC}^2\)
\(\mathrm{AB}^2=\left(\displaystyle\dfrac{1}{2}\right)^2+\left(\displaystyle 1-\dfrac{\sqrt{3}}{2}\right)^2\)
\(\mathrm{AB}^2=\dfrac{1}{4}+1-\sqrt{3}+\dfrac{3}{4}\)
\(\mathrm{AB}^2=2-\sqrt{3}\)
ここで電卓を使って、\(2-\sqrt{3}\) は、およそ0.267949だから
\(\mathrm{AB} \fallingdotseq \sqrt{0.267949} \fallingdotseq 0.518\)
ふう。やっと多角形の1辺の長さが出た。これを12倍して、直径でわると
\((0.518 \times 12)\div 2=3.108\)
ルーロー、どう? さっきより、かなり3.14に近づいた!
はるかさん、おつかれさま! 小さなアルキメデスだね。アルキメデスは正96角形を元に円周率を計算して、3.14に近い数字を導き出したんだ。古代ギリシア時代、紀元前3世紀頃のことだよ。中国の三国時代にも劉徽(りゅうき)という数学者がいて、正192角形まで使って3.14159という数字を求めたと書き残している。こちらは、西暦263年の本だ。
ひゃ、192角形?! 今日は自分でも計算してみたから、いっそうすごさがわかるな。まさに情熱と根気だね。
*和傘/番傘(ばんがさ)、蛇の目傘(じゃのめがさ)、野点傘(のだてがさ)などさまざまな種類があり、雨よけのほか、歌舞伎や踊りの小道具、屋外での日よけなどにも使われている。
岐阜県岐阜市
その他のコンテンツ
