今週の算数・数学フォト

ひろとです。今日はルーローと、兵庫県西宮市の「熊野神社」にやってきたよ。ここは「甲子園熊野神社」とも呼ばれているんだって。……あれ？境内に、小さな神社を見つけたよ。名前は「算学神社」だって。もしかして、数学に関係のある神社なのかな。

あっ。両わきの模様が、そろばんの珠みたい。文字の方は……「碑彰顕算和」？　よくわからないけど、やっぱり算数と関係がありそうだね。

あっ。江戸時代といえば、鎖国の時代！

石碑の台座に書いてある図も、気になるな。図形の問題みたい。

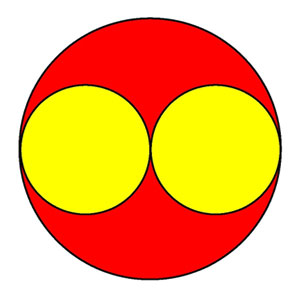
うーん、そうだなぁ。相似比を使ったらどうだろう？
大きい円と小さい円は、もちろん相似だ。小さい円の半径は、大きい円の半径の\(\dfrac{1}{2}\)。つまり、大きい円と小さい円の相似比は1:\(\dfrac{1}{2}\)になる。
面積比は相似比の2乗だから、1:\(\dfrac{1}{4}\)だね。
黄色い部分の面積は、小さい円の2つ分だから、大きい円と黄色い部分の面積比は、1:\(\dfrac{1}{2}\)。
赤い部分の面積は大きい円の面積から黄色い部分の面積を引いたものだから、大きい円の面積の\(\dfrac{1}{2}\) 。
ということは、赤い部分と黄色い部分の面積は、等しいよ！

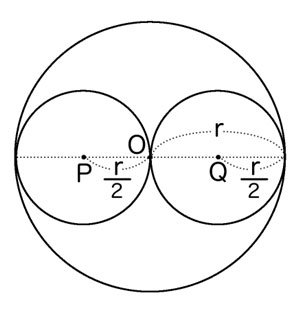
別の方法も、思いついちゃった。今度は、文字を使うよ。
大きい円Oの半径をrとすると、小さい円P、円Qの半径はそれぞれ\(\dfrac{r}{2}\)。だから、円Oの面積は\(\pi r^2\)。円Pと円Qの面積はどちらも\(\dfrac{\pi}{4}r^2\)だから、黄色い部分の面積は\(\dfrac{\pi}{2}r^2\)
ということは、赤い部分の面積は\(\pi r^2−\dfrac{\pi}{2}r^2\)で、\(\dfrac{\pi}{2}r^2\)となる。うん。やっぱり2つの面積は等しいね！

今日はたまたま、すぐに答えがわかったけどさ。例えば、もっとずっと難しくて長く考え続けた問題が解けたとしたら、神様に感謝したくなったり、解法を大きく書いてみんなに見せたくなったりする気持ちは、すごくよくわかるよ。江戸時代の人たちも、やっぱり同じだったんだね。