今週の算数・数学フォト
- TOP
- 今週の算数・数学フォト
- 鹿児島の富士山
開聞岳
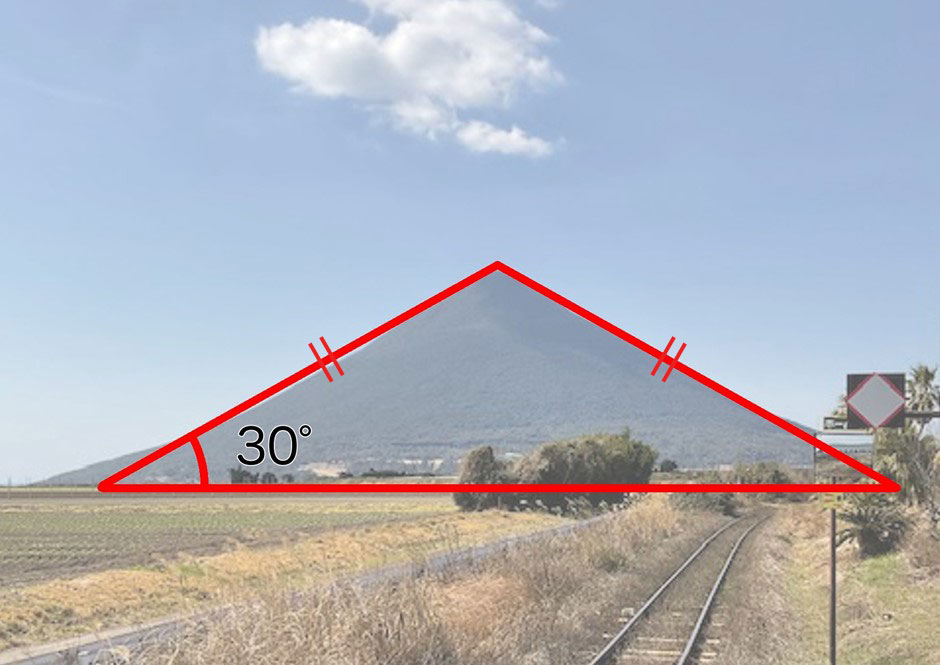
ゆうなです。ここは、鹿児島県指宿（いぶすき）市のJR西大山駅。JRの駅では、日本最南端なんだよね。三角形の山がくっきり、きれいだね。
よく知っているなぁ。さすが、鉄道好きのゆうなさんだね。そして向こうに見えるのは、開聞岳（かいもんだけ）という名前の山だよ。標高は924m。
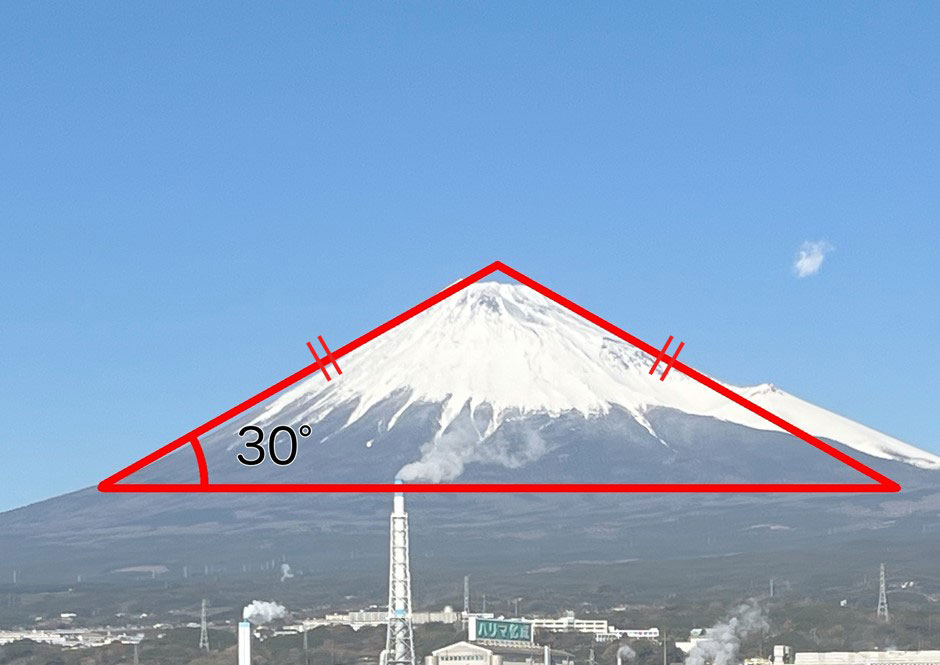
それにしても、本当にキレイな三角形。なんだか、富士山に似ているような。
いいところに気づいたね。実は開聞岳は、「薩摩富士」とも呼ばれているんだ。ゆうなさんはどうして「似ている」と思ったのかな？
へええ。鹿児島の富士山なんだね。
「似ている」って思ったのは、まず、山の形がキレイな二等辺三角形に見えること。これは共通しているよね。あとは……そうだ、斜面の角度かな？
いいね！すごくいい目のつけ所だよ。この山を二等辺三角形とみなして、おおよその角度を調べてみようか。写真を使えば、測りやすいよ。
OK！これが写真だね。ええと、まず開聞岳の斜面の角度は……30°くらいだ。富士山の方は……あっ、やっぱり30°くらいだよ。なるほど、だから２つの山が、似て見えるわけだね。
そう、横から見ると二等辺三角形。でもね、山を真上から見たら、どうかな。飛行機から撮った、富士山の写真を見たことはある？
そういえば、富士山を真上から見ると、円形だよね。もしかして、火山だからかな？ てっぺんから吹き出した溶岩が流れて、こんなにキレイな形になったのかも。
うん、確かにそれが、富士山の成り立ちだよ。ゆうなさん、さすが！ さらに、山を立体図形として考えるなら、直角三角形を360°回転させてできた、回転体に近い形と見ることもできる。つまり、「円錐」だね。
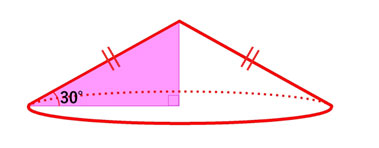
富士山って、平らな円錐なのか。なるほど！
そう。開聞岳も上から見ると円形で円錐の形をしているよ。そして、このような富士山……つまり、「○○富士」と呼ばれる山は、なんと全国に300以上もあるんだよ。有名なのは、青森県の津軽富士（=岩木山）や、北海道の蝦夷富士（=羊蹄山 ようていざん）だ。
へええ、北海道にまで！ 日本最北端のJRの駅は、もちろん北海道。稚内（わっかない）駅だよ。鹿児島から北海道まで、「富士山」がびっしり並んでいるんだね。羊蹄山って、北海道のどの辺りにあるんだろう。調べてみなくちゃ！
＊開聞岳／鹿児島県指宿市
〒891-0603 鹿児島県指宿市開聞十町
その他のコンテンツ