今週の算数・数学フォト
- TOP
- 今週の算数・数学フォト
- 渦巻きは、作図できる？
渦潮
そうたです。ここは徳島県の「鳴門海峡」です。海が渦巻いてる！大迫力だ。ルーロー、すごい眺めだねぇ！
これが鳴門の渦潮だよ。鳴門海峡は幅が狭くて、潮の満ち引きのたびに、激しい川みたいな流れが起こるんだ。そして、最大で時速約20kmになる速い流れとその両側の遅い流れの間に、渦が発生する。渦の大きさは、直径20mになることもあるんだって。
天気図で見る、台風の渦巻きみたいだな。こんなにきれいな渦巻きが、自然にできるんだから不思議だね。
確かに！台風に似ているよね。渦巻き模様のもの、他にも何か思いつくかな？
アンモナイトやオウムガイも、渦巻きだね。身近なところでは、蚊取り線香とか。でも、蚊取り線香の渦巻きは、渦潮や台風の渦巻きとは少し違う気もするな。何が違うんだろう？
さすがそうたさん、なかなか鋭い気づきだね！実は、曲線の種類が違うんだよ。外側ではゆるかったカーブが、中心に向かうにつれてクルクルとキツくなっていくのが、渦潮や台風の曲線。でも、蚊取り線香の曲線は、螺旋（らせん）の幅が一定だよ。名前もかっこよくて、「アルキメデスの螺旋」というんだ。
あっ。「アルキメデスの原理」の、アルキメデスかな？
その通り！アルキメデスは、螺旋の研究もしていたんだね。
一方、台風や渦潮の曲線は、「等角螺旋」と呼ばれているよ。
へえぇ。渦巻きにも種類があるのか。自分でかいてみたら、もっと仲良くできるというか……納得できるかもしれない。作図できるかな。たとえばアルキメデスの螺旋は、幅が一定。つまり等間隔だよね。コンパスをうまく使えないかな……うーん……。
いいね、そうたさん！コンパスを使って、アルキメデスの螺旋に似た曲線をかくことができるよ。この図を見てみて。まず、点Aを中心に、半径ABの半円をかくよ。それから、中心を点Bに変えて、今度は半径BCの半円をかく。
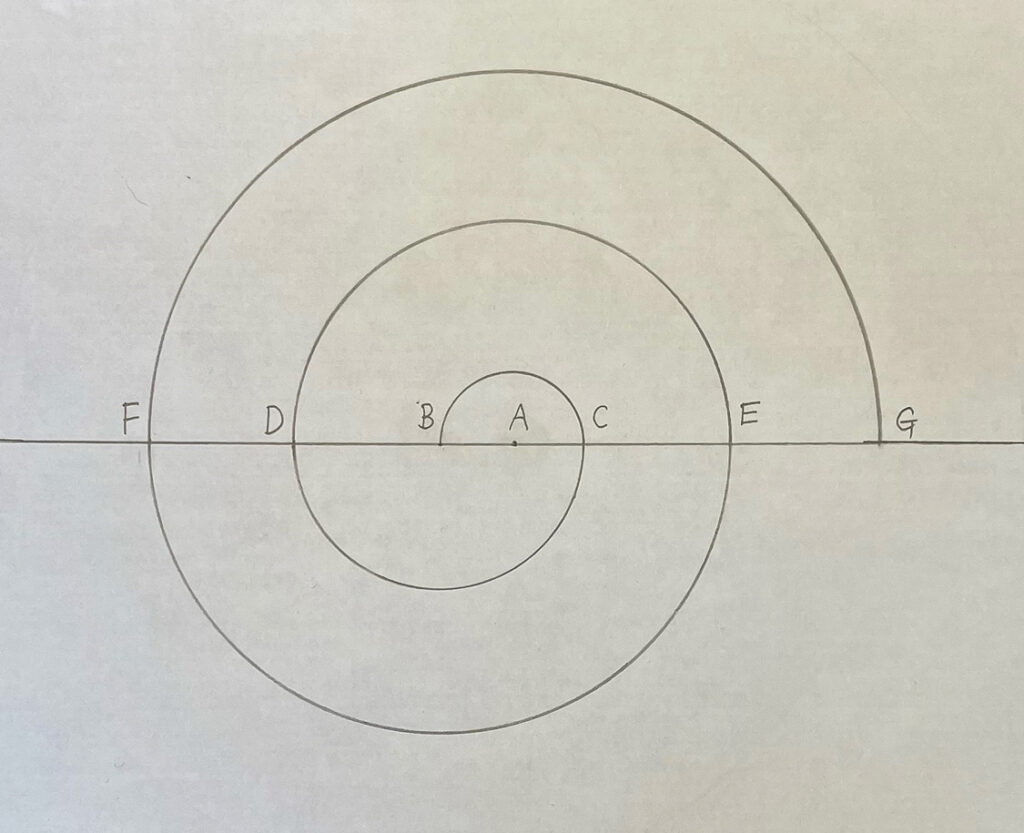
なるほど！次は、また点Aを中心として、半径ADの半円をかくんだね。ABの長さを1とすると、半円をかくたびごとに半径が1ずつ増えていく。これなら、螺旋の幅がほぼ等間隔になるね。
もっと正確にかくなら、糸巻を使った、こんな方法もあるよ。
こういうの、いいなぁ。やってみたくなるね。じゃあ、この渦潮の曲線、等角螺旋の方は？もう少し難しそうだな。
ふふふふ、ヒントは「黄金比」だよ。帰ったら調べてみて！数学者たちは、昔から、自然の中のさまざまな形を解明してきたんだね。
＊渦潮／徳島県鳴門市
〒772-0000 徳島県鳴門市
その他のコンテンツ