今週の算数・数学フォト
- TOP
- 今週の算数・数学フォト
- 不思議な模様に夢中
萩・石見空港
うーん。これはなんとも、本当に……本当に、きれいな模様だね……どうなってるのかな……。
ますりんです。今日は、しほさんと島根県の「萩・石見空港」にやってきたんだけど。しほさん、さっきからずっと組子細工の前から動かないんだよ。
組子細工というのは、釘を一本も使わずに小さな木片を組み合わせて、とっても繊細な模様を描き出す伝統技術だよ。ここに飾られたアート作品「春の高津川」は、わずか数センチの木片が5万個以上も組み合わされて出来ているんだ。
ねえねえ、ますりん！ 私もこういう模様を、かいてみたいな。三角形がすきまなくならんでいるね。1つの三角形の3辺の長さはどれも等しそうだから、正三角形かな。ということは、全部の角の大きさが同じだよね。三角形の3つの角の大きさの和は\(180^{\circ}\)だから、\(180^{\circ} \div 3=60^{\circ}\)でしょう？ 分度器を使ってかけば、ほら、こんな感じ。
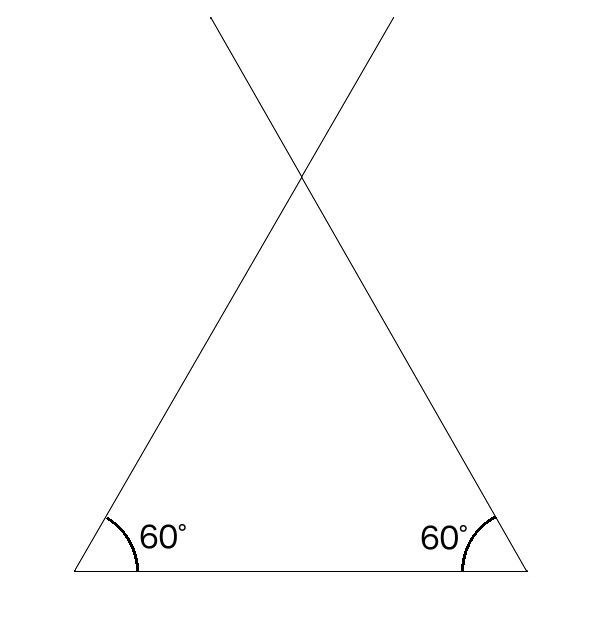
おっと！ すごい勢いだ。自分でかいてみるっていうのは、いいね。しかも、たくさん並んだ図形にも気づいたんだ。すごいね、しほさん。せっかくだから、正三角形の他のかきかたも考えてみる？
えっ、他のかきかた？ うーん、正三角形のことを、もう少し考えてみればいいのかな？ 3つの辺の長さがみんな同じだから、コンパスを使ってかくこともできるけど……。
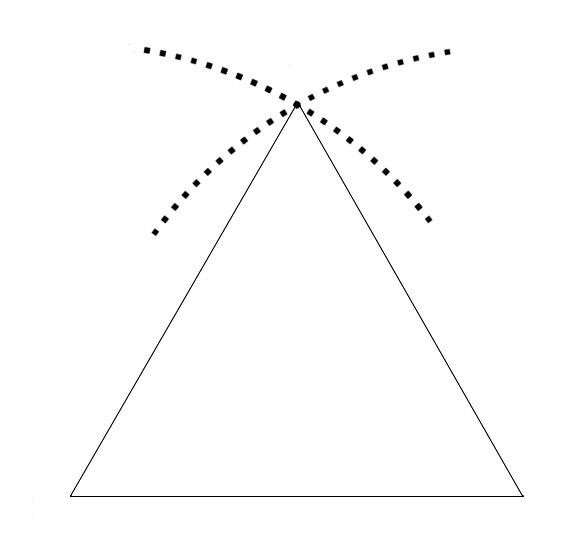
ふふふふ、実はね、しほさん。このときに、コンパスで長さをうつしとるだけじゃなくてぐるりと円をかいてみると、不思議なことが起こるよ。
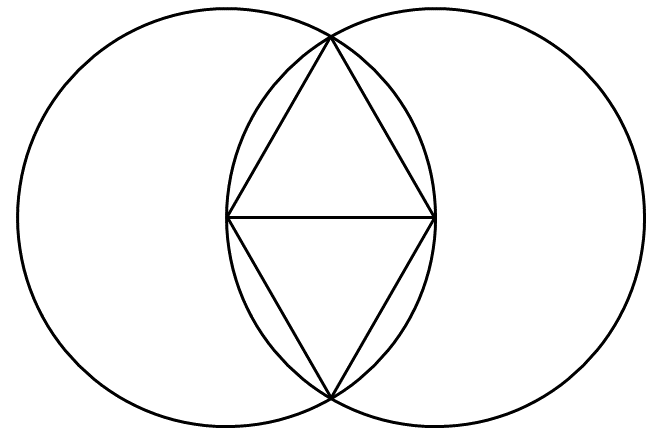
さらに、横にどんどん、円をつなげていってみようか。さあ、どうなる？
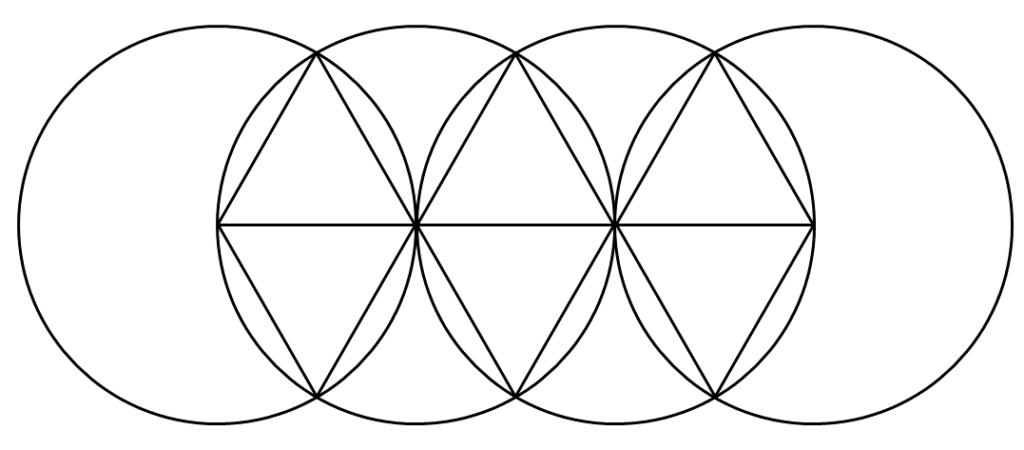
ああっ、組子細工の模様があらわれた！ これなの、こういうのが、かいてみたかったの。すごいなぁ。コンパスが決め手だったんだね。
これは「七宝亀甲（しっぽうきっこう）」といって、ずっと昔からある縁起のいい模様なんだよ。他にも、いろいろな円と線をかいてみてね。コンパスと定規だけで、きっとまだまだ遊べるよ。
＊萩・石見空港／島根県益田市。アート組子作品「Takatsu River in Spring〜春の高津川」の制作は、吉原木工所。2020年にお目見えした。
〒698-0051 島根県益田市内田町
その他のコンテンツ