特集記事（小中学校）

相模原市立相武台中学校
加藤光顕先生

Dマークコンテンツ「ドミノ倒しを見てみよう」はこちら

Dマークコンテンツ「パズルで長方形をつくろう」はこちら

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。

①動画で簡単に事象の確認！数学を使って事象の解明へ！

□単元：1章　多項式　　□内容：p.10　多項式の計算　　□学年：中学3年

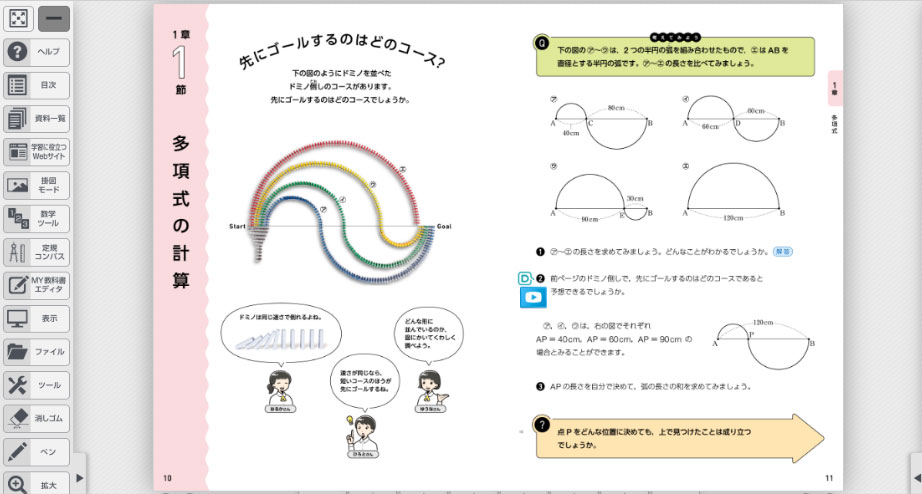
教科書では、㋐～㋓の長さを求めてから予想を立てる流れとなりますが、生徒が答えを知りたがっていたので、先に実際の結果を見せることにしました。Dマークコンテンツを活用すると、実際の実験映像を動画で確認することができます。生徒にDマークコンテンツ「ドミノ倒しを見てみよう」の動画を見せると、「あ！一緒だ！」「なんで！？」という声が挙がりました。「なぜ？」が出てきたら、チャンスです。具体的な数字を使ってコースの長さを求めて調べること、文字で説明することにつなげることができるからです。

②シミュレーションでパズルを操作することで、多項式の因数分解を感覚でつかむ

□単元：1章　多項式　　□内容：p.23　因数分解　　□学年：中学3年

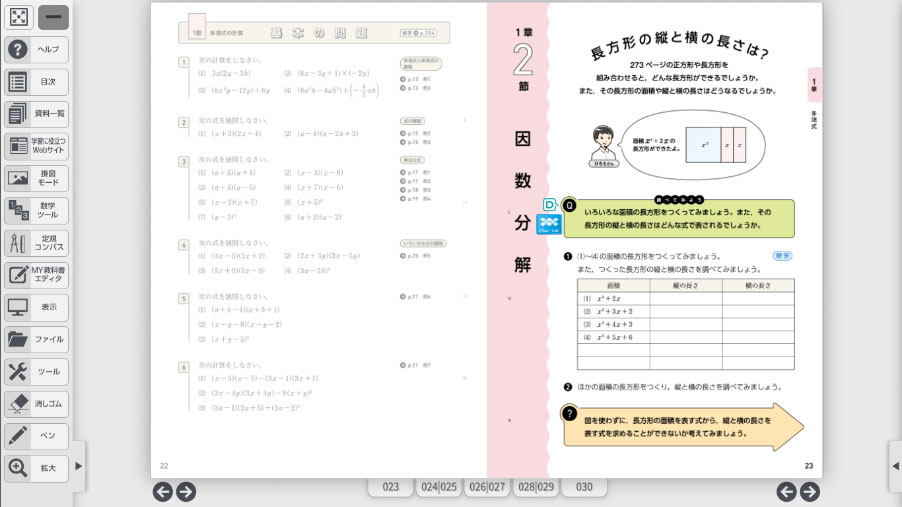
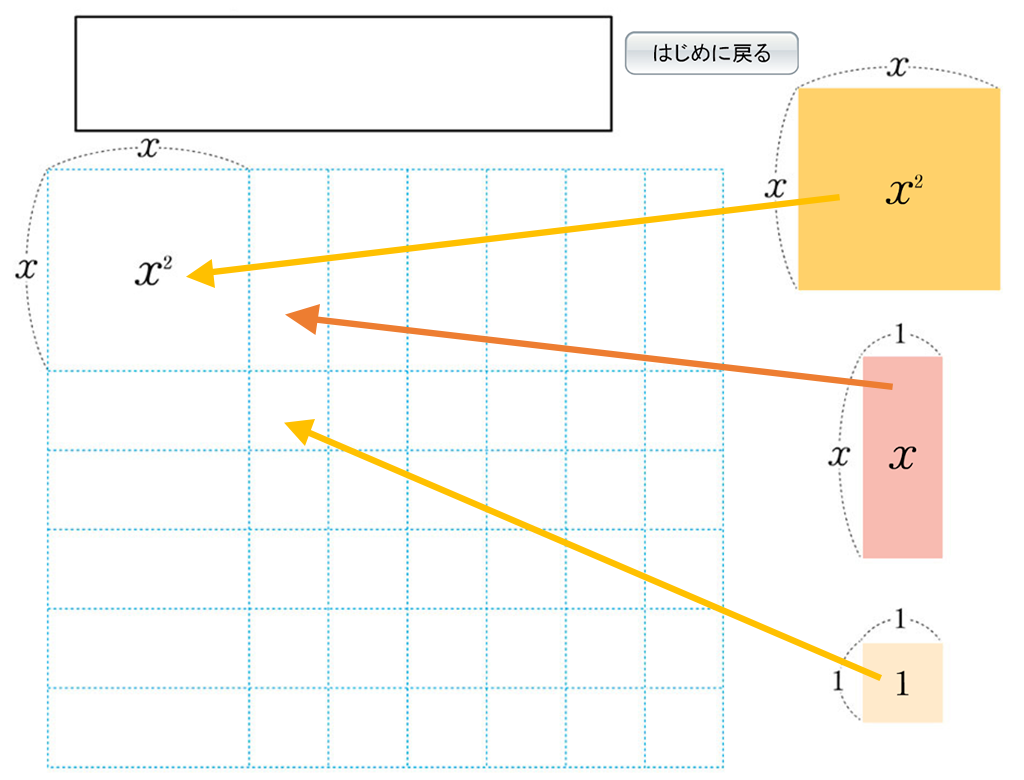
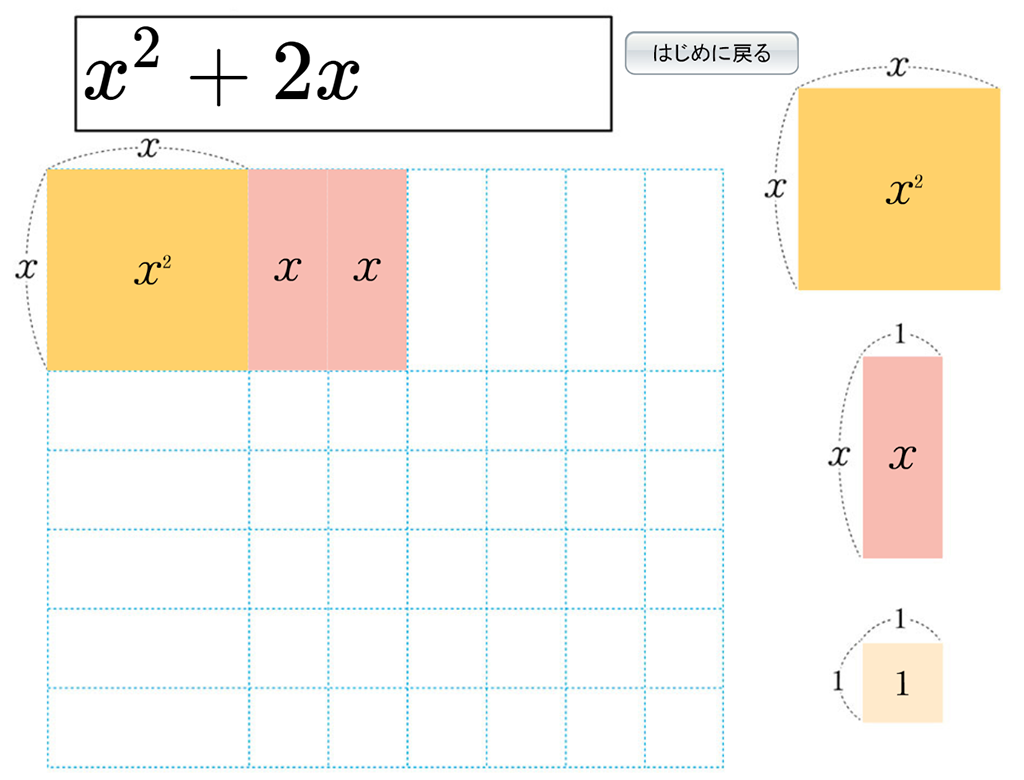
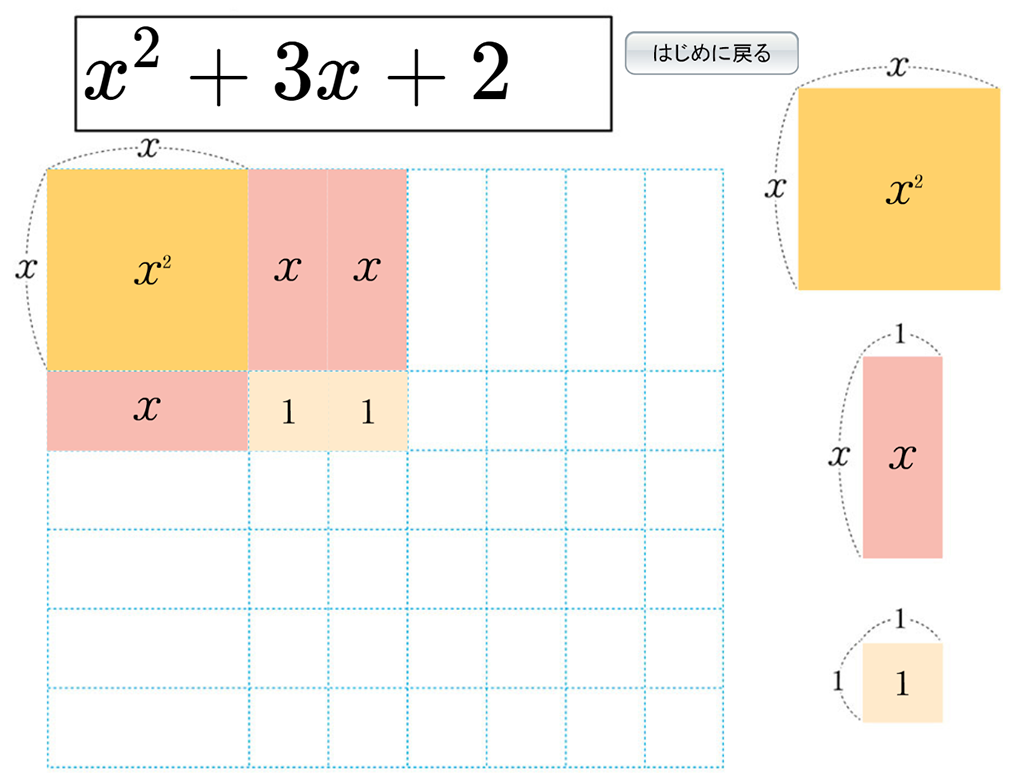
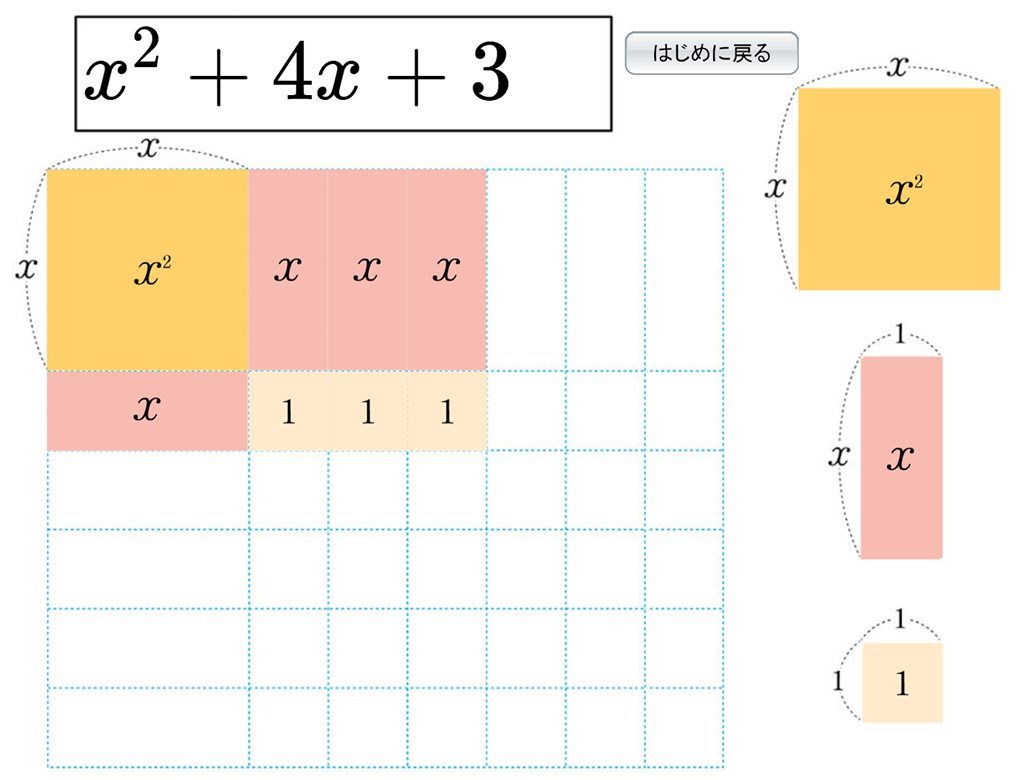
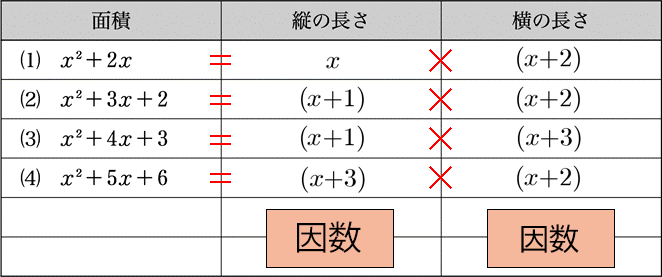
　1年で既習の因数分解と素因数分解をもとに、今度は文字式で表のように縦と横の長さを求めていきます。表を使うことで、面積と縦と横の長さとの関係を確認することが容易にできます。そして、その表が因数分解を表していることに気づかせることができます。

③まとめ

　今回紹介した内容は決して応用問題ではなく、それぞれ単元の導入部分となります。しかも多項式の計算です。多項式の計算は、やり方さえ覚えてしまえば、あとはそのルールに沿って解くだけで答えにたどり着くことができるかもしれません。しかし、それでは本当の理解とは言えません。「なぜそうなるのか？」という問いを日頃から大切にして、計算だからこそ揺るぎないそのしくみを考えさせることが大切です。そうすることが用語の理解をはじめ、やがては高次的、発展的な計算、汎用的な考え方につながるのだと私は考えています。