特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【ICT教育のイマ】クロームブック活用術 実践㊽~…
中学校
2024.01.18
【ICT教育のイマ】クロームブック活用術 実践㊽~デジタル教科書/操作編(3年 三平方の定理⑤)~
相模原市立相武台中学校
加藤光顕先生
今回は、3年三平方の定理の学習で活用したデジタル教科書の有効な方法をご紹介します。

①シミュレーションで糸の最短経路を簡単にイメージできる
□単元:7章 三平方の定理 □内容:p.203 三平方の定理の利用 □学年:中学3年
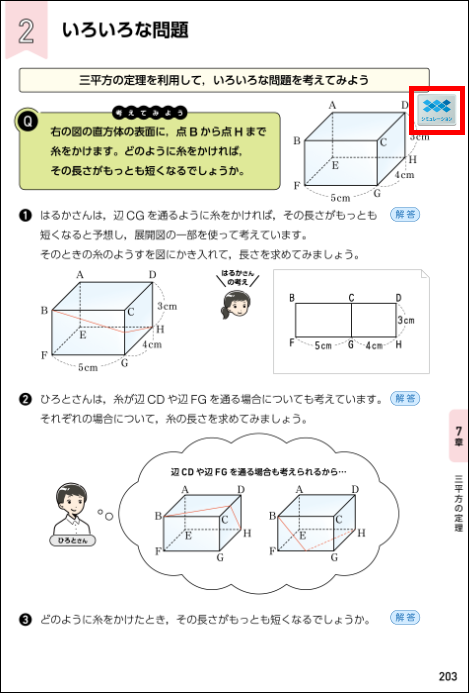
教科書p.203は、立体図形の表面に糸をかけて、その長さがもっとも短くなる場合を考えます。中学1年でも空間図形の章で、最短になる場合を考えてきましたが、中学3年では三平方の定理を学んだことによって、さらにその長さを求めることができるようになります。
ここでまず大切なのは、糸がどのようにかけられるか、その経路です。空間図形の表面を通るので、展開図から「糸がどのような経路で結ばれるか」、また「最短なのでスタートの点からゴールの点まで直線になる」ことの理解が、解決のステップとなります。さらに「直線になる」といっても、どの辺を通るかによって長さは変わります。ここでは、辺 \(\text{CD}\)、辺 \(\text{CG}\)、辺 \(\text{FG}\) を通る場合の最短経路を考えていきます。
この状況を確認する際には、デジタル教科書のシミュレーションが有効です。図が表示され、点を自由に動かすことができます。また、その際の糸の長さも自動で表示されるので、生徒は問題の概要についてイメージすることができます。
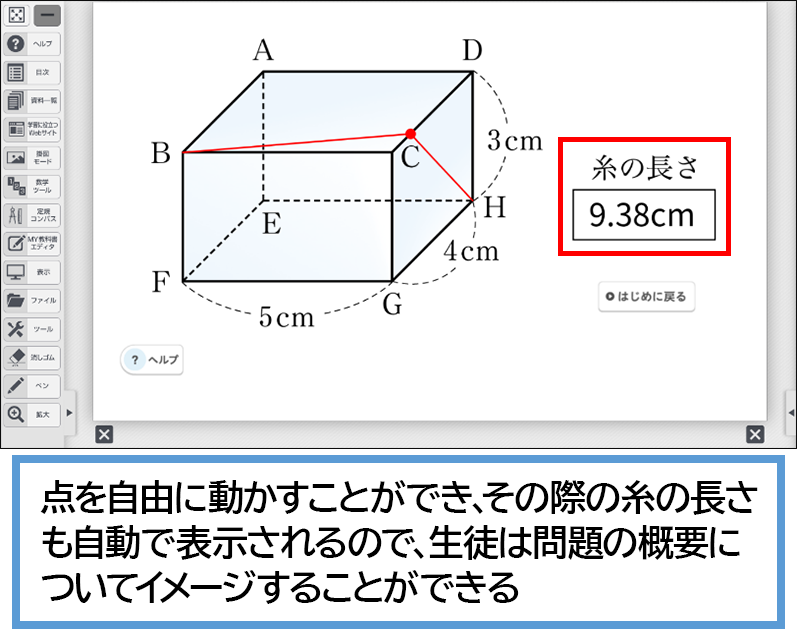
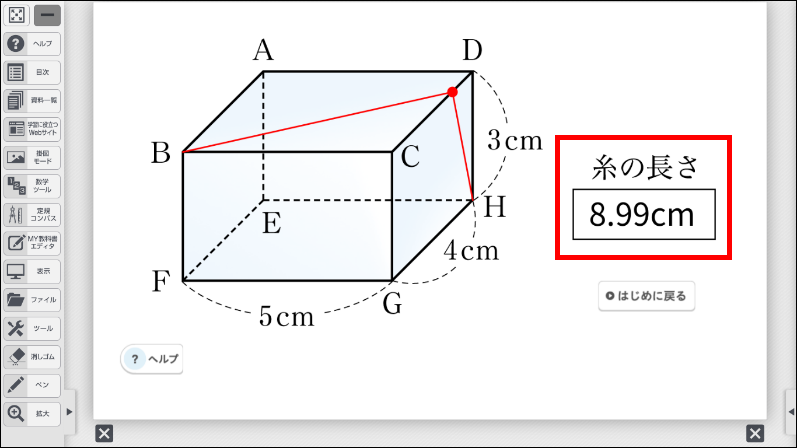
辺 \(\text{CD}\) を通る場合では、なかには点が \(\text{C}\) や \(\text{D}\) になるときが、いちばん短くなると直感的に考える生徒もいます。そのような場合は、点を \(\text{C}\) や \(\text{D}\) に動かすことで、最短経路にならないことを容易に示すことができます。
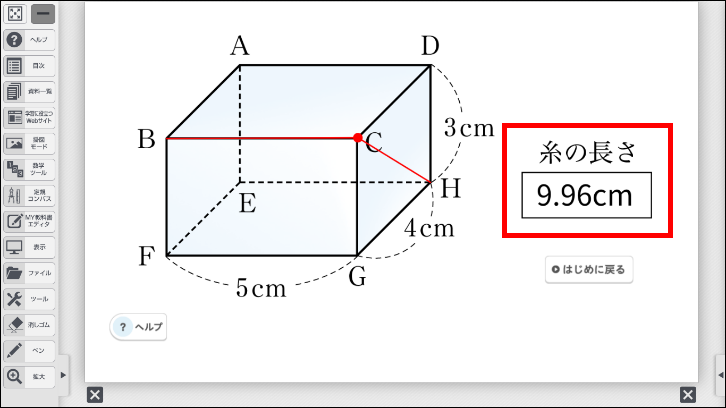
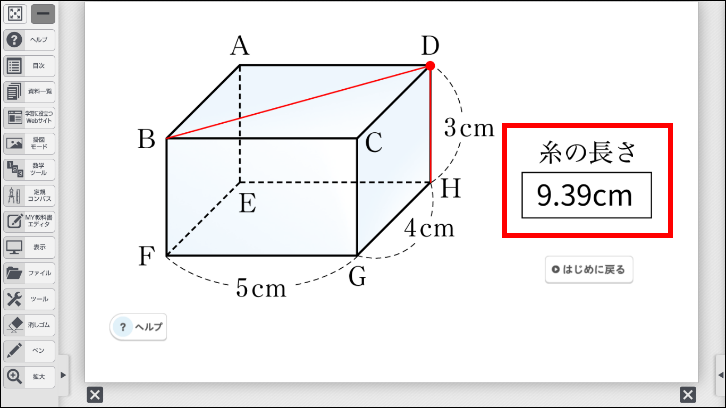
点は辺 \(\text{CD}\) 上だけでなく、辺 \(\text{CG}\)、辺 \(\text{FG}\) 上にも動かすことができます。
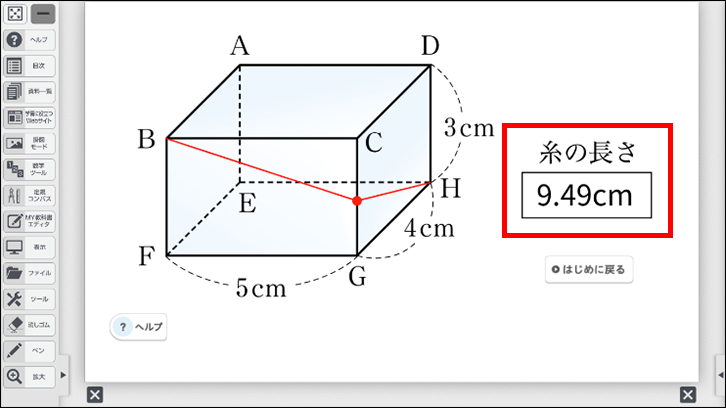
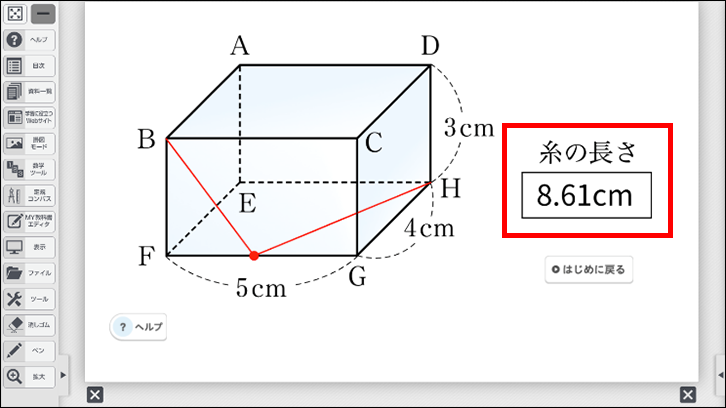
このシミュレーションで糸の経路がイメージできれば、展開図を考える際にも「どことどこの点を直線で結べばよいか」を想像することができるようになります。想像ができれば、糸の直線を斜辺とする直角三角形を見いだすことができ、三平方の定理を利用する段階へ進むことができます。
従来は、この段階へ進む前の「糸の経路をイメージすること」に苦戦する生徒が多くいました。私も黒板や紙で提示して確認していましたが、経路によっては線を付け足すか、他の図を準備しなくてはなりませんでした。また線をひくのに失敗すると、汚くなったり、線が多くてわかりづらくなったりすることもありました。線の長さで比較することもできません。
しかし、デジタルコンテンツになったことで、何度もやり直しができ、いろいろな経路を簡単に確認できるようになったので、生徒にとって非常にわかりやすくなりました。実際に、多くの生徒がこのシミュレーションを通して、納得して課題に取り組めるようになりました。ぜひ、活用してみてはいかがでしょうか。
その他のコンテンツ
