特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【ICT教育のイマ】クロームブック活用術 実践㉖~…
中学校
2023.09.05
【ICT教育のイマ】クロームブック活用術 実践㉖~デジタル教科書/操作編(3年 関数\(y=ax^2\)②)~
相模原市立相武台中学校
加藤光顕先生
今回は、3年で学習する関数\(y=ax^2\)のグラフの実践で活用したデジタル教科書の有効な方法をご紹介します。

①シミュレーションでグラフのしくみを容易に確認する
□単元:4章 関数\(y=ax^2\) □内容:p.103 関数 \(y=ax^2\)のグラフ □学年:中学3年
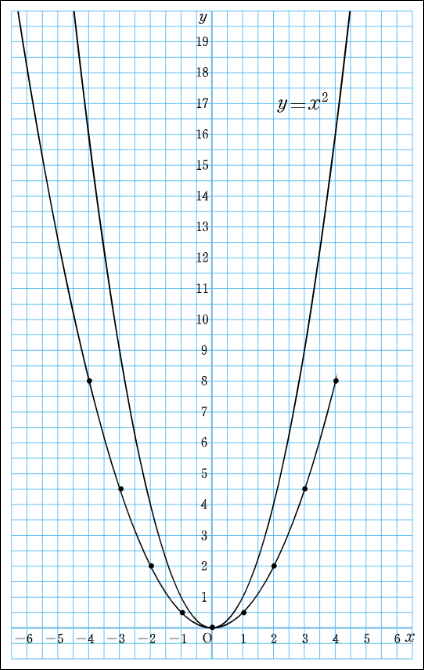
教科書p.103では、関数\(y=ax^2\)の\(a\)の値が変わるとき、グラフはどのようになるのかについて、\(y=x^2\)と\(y=2x^2\)を比較して調べています。
調べる際に、点の取り方や\(x\)と\(y\)の値がわからない生徒も見られることがあります。そのようなときに有効なのが、デジタル教科書のシミュレーションです。
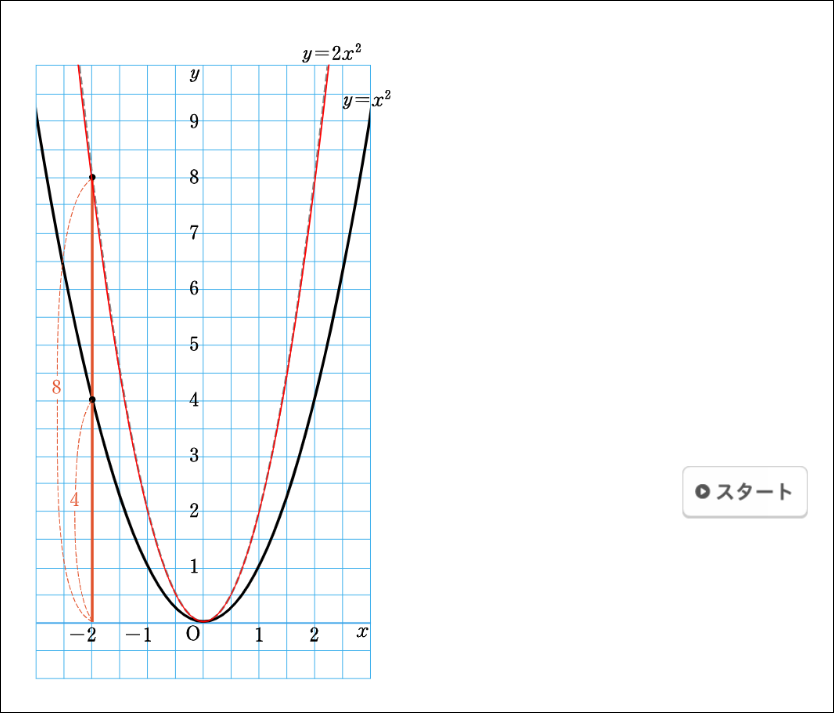
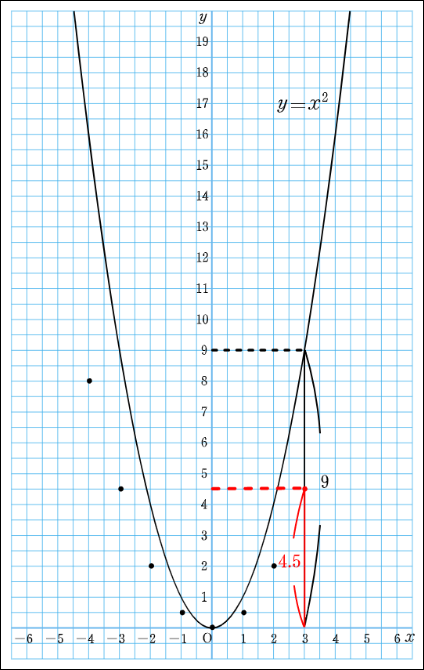
本コンテンツでは、\(y=ax^2\)と \(x=-2\)のグラフにおいて、\(x=-2\)に対応するそれぞれの\(y\)の値を赤色で表示させることから始めて、順に\(x\)の値を変えながらそれぞれの\(y\)の値を表示させていきます。最後に、点を結び\(y=2x^2\)のグラフをえがくことで、\(y=x^2\)のグラフと比べながら、違いを確認することができるようになっています。生徒は違いを比較しながらグラフの特徴を考えることができるでしょう。
思い出せば、以前は小黒板にチョークでかいて説明していました。しかし、見えづらい生徒がいたり、準備に手間がかかったりしていました。また、一度かいてしまうと、やり直しができないため、見逃してしまう生徒も多くいたはずです。
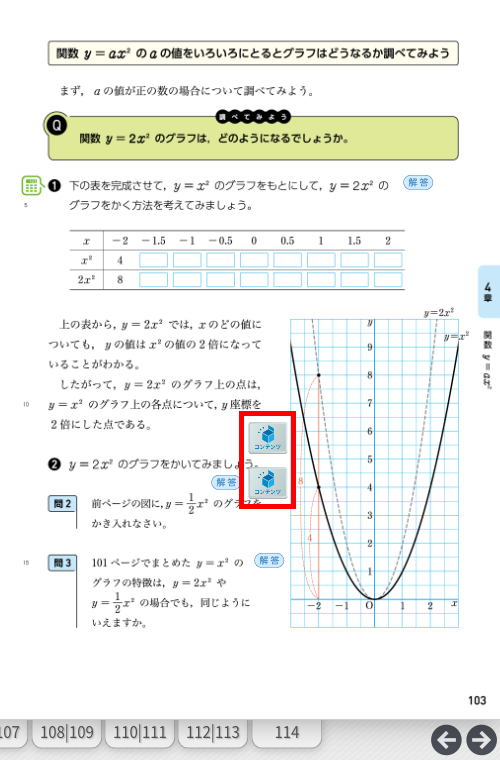
しかし、デジタルコンテンツなら、準備するのはクロームブックだけです。また、デジタルのよさは、何度もやり直しができ、途中で止めることもできることです。これによって、あらゆる生徒が見逃すことなく確認することができるようになりました。
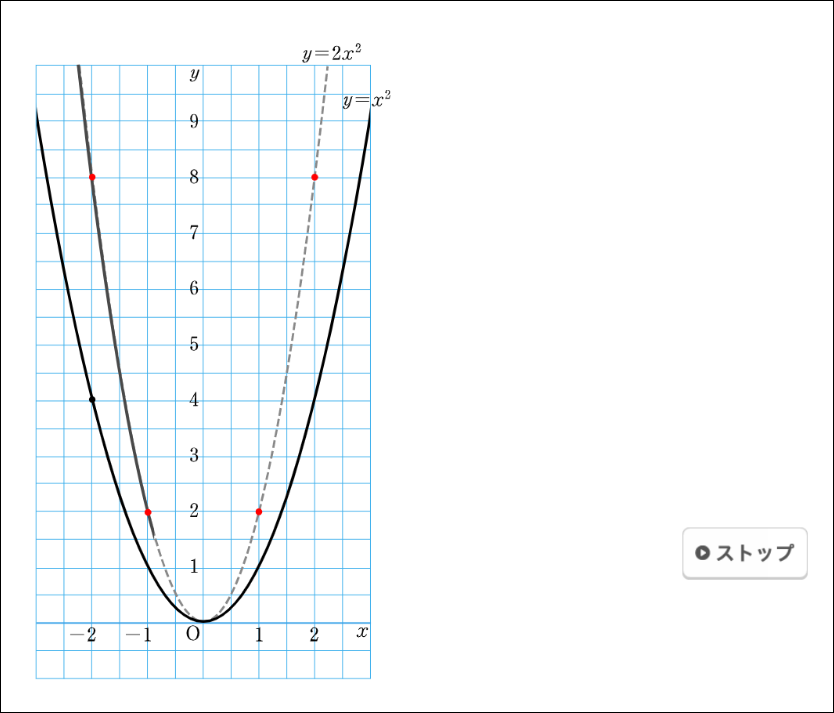
問2にある、\(a\)の値が分数をとるグラフについても、シミュレーションで確認することができます。\(y\)の値が小数になると、どうしても抵抗感を示す生徒がいますが、「シミュレーションで表すと理解しやすかった」と答えてくれた生徒が多くいました。


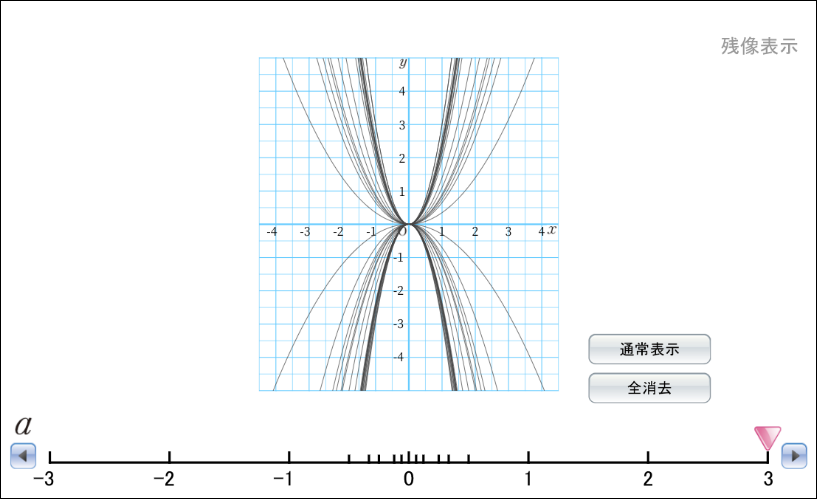
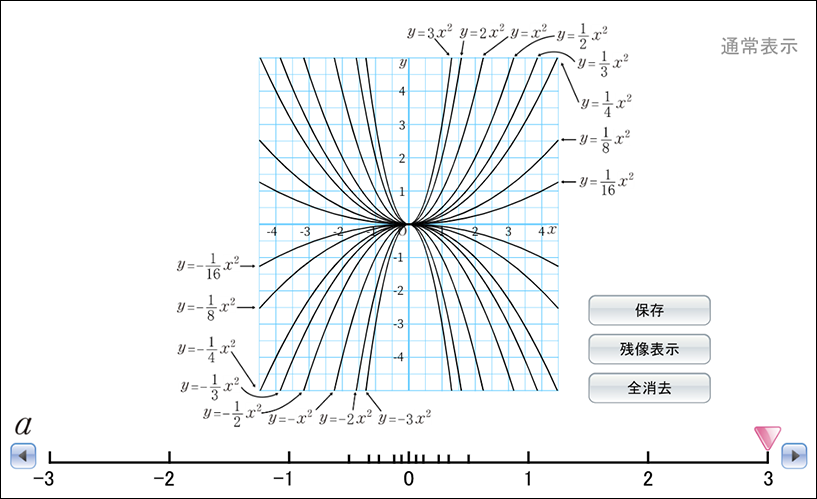
②シミュレーションで\(a\)の値とグラフの関係を確かめる
□単元:4章 関数\(y=ax^2\) □内容:p.106 関数 \(y=ax^2\)のグラフ □学年:中学3年
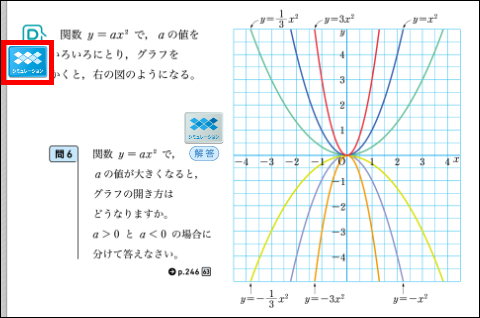
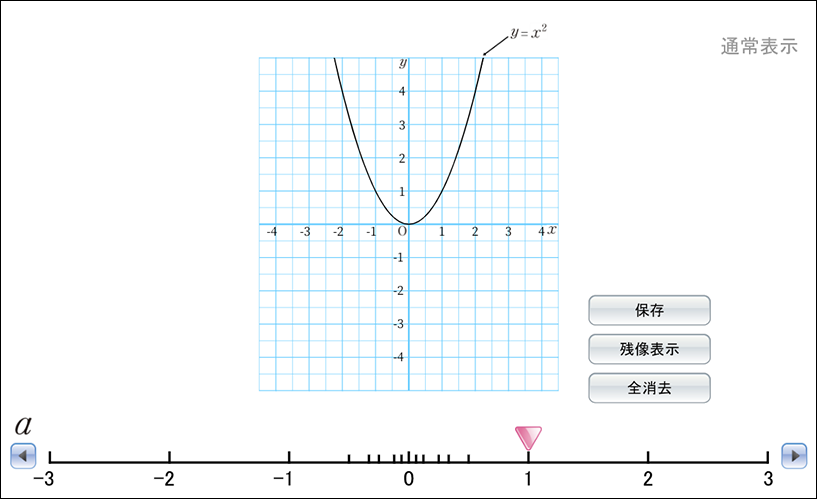
教科書p.106のシミュレーションでは、\(y=ax^2\)の\(a\)の値をいろいろにとり、グラフを確かめることができます。
値を指定して確かめることができるため、\(a\)の値が正の数、負の数、分数など、正負や絶対値が変化することでグラフの形がどのように変化するのかを可視化できます。わざわざ計算して点をプロットし、線をひかなくても容易にグラフの形を確認できるのも、デジタルのよさと言えます。以前は、この作業に膨大な時間と手間を費やしていました。
また、「残像表示」に「✔」を入れると、グラフの残像を表示することもできるため、左右対称となるグラフの変化を容易に可視化できます。
③まとめ
今回は、中学3年の関数\(y=ax^2\)のグラフにおける、デジタルコンテンツの有効性を紹介しました。デジタルだからこそ、容易かつ効率的に確認することができます。以前は、実際に生徒に計算させ、手書きさせていたため、膨大な時間を費やしていました。もちろん、その過程も大切な取り組みですが、個人差もあり、本来考えさせたい\(a\)の値とグラフとの関係を調べるまでに挫折してしまう生徒も少なくありませんでした。そのような生徒の取り組みをサポートするうえでも、デジタルコンテンツは重要なツールとなるのではないでしょうか。
その他のコンテンツ
