特集記事（小中学校）

広島経済大学
准教授　青谷章弘先生

この記事の流れ

1. GeoGebraを用いて探究的な活動を行うことで、図形の性質を見いだしたり、定理の表現を理解しやすくなることを提案します。
2. GeoGebraの簡単な紹介をします。Webサイトから利用できます。
3. 具体的な例として、「円周角の定理の逆」の下線部分（後述）の理解が難しい点を解消するためにGeoGebraを用いる授業を紹介します。この授業には次の①、②のよさがあります。
   ①GeoGebraを用いて、円周上の2点からつくった角が等しくなる点を探す活動を行うと、その点の集合が雪だるま型の図形になることを容易に見いだせます。
   ②「円周角の定理の逆」の下線部分の必要性を感得することができます。

１　この記事で提案したいことの概要

　この記事で提案する授業の主目的は、「円周角の定理の逆」の発見です。「円周角の定理の逆」は、教科書には次のように書かれています。

　GeoGebraを用いて、円周上にある2点からつくった角が等しくなる点を探す活動を行うと、その点の集合が雪だるま型の図形になることを容易に見いだせます。このことを一般化すると、「∠APB＝∠AＱBならば、4点A、B、Ｐ、Qは雪だるま型の図形上にある」となります。一方、教科書では下線部の条件があるため、4点が雪だるま型の図形上ではなく、円周上にあるという結論になっています。定理の結論を簡潔にするために、仮定に条件が加えられていることがわかります。

２　GeoGebraの簡単な紹介

　GeoGebraは、Webサイト上で、無料で使用することができます。パソコンにインストールする必要もありません。

　インターネット上で「GeoGebra」と検索し、GeoGebraのWebサイトにアクセスしたら「アプリの開始」ボタンを押します。今回は図形を描画したいので、画面上部のプルダウンメニューから「幾何」を選択します。

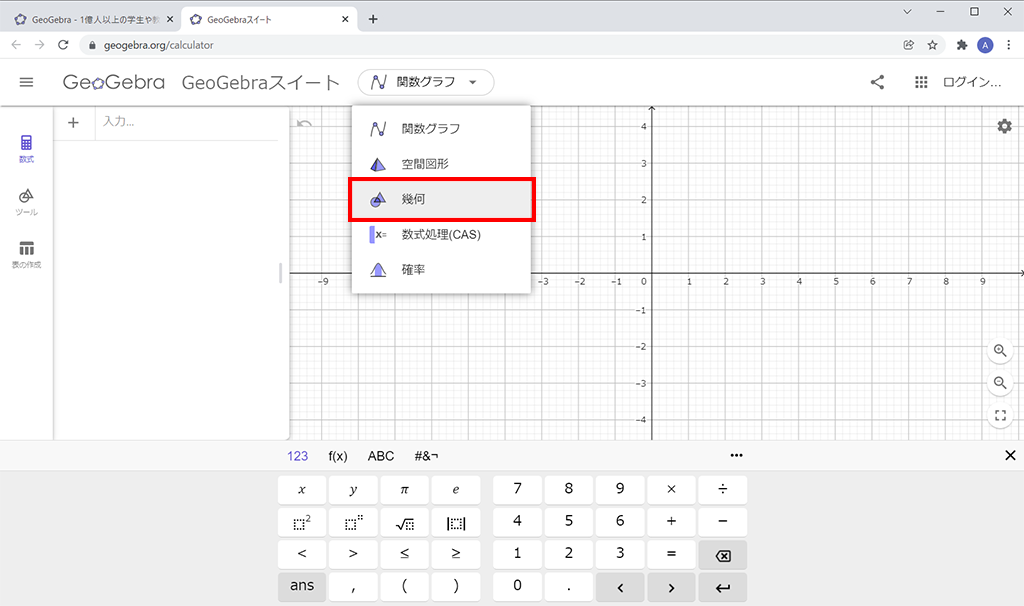
　画面左側の「基本ツール」メニューから「中心と1点で決まる円」を選択し、中心と他の1点を指定すると、円が描かれます。

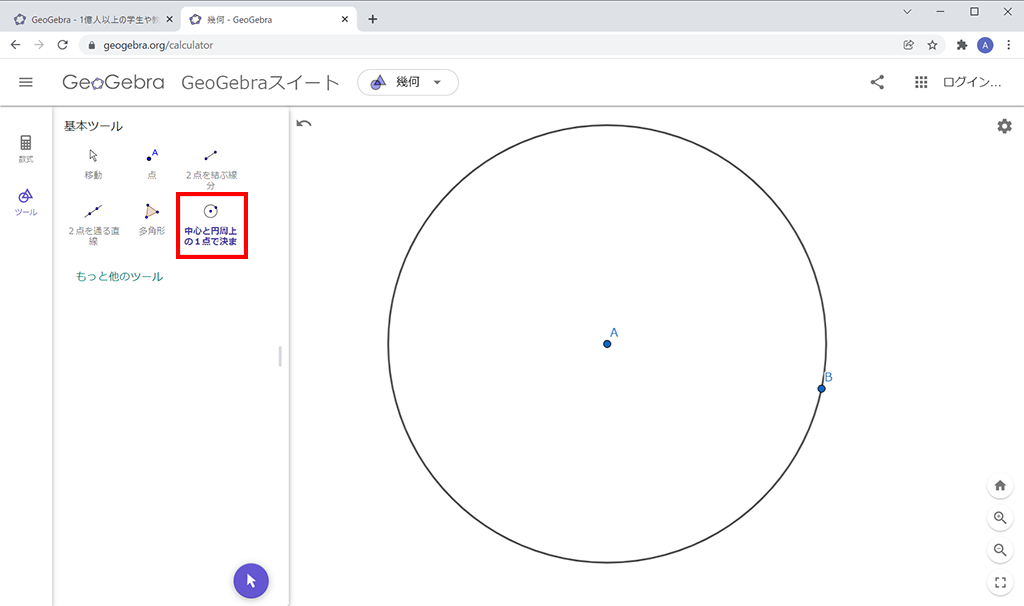
　「基本ツール」メニューで「点」を選択し、円周上に3点C、D、Eをとります。作成した点はあとから自由に動かすことができます。このとき、円周上にとられた点は円周上のみを動きます。

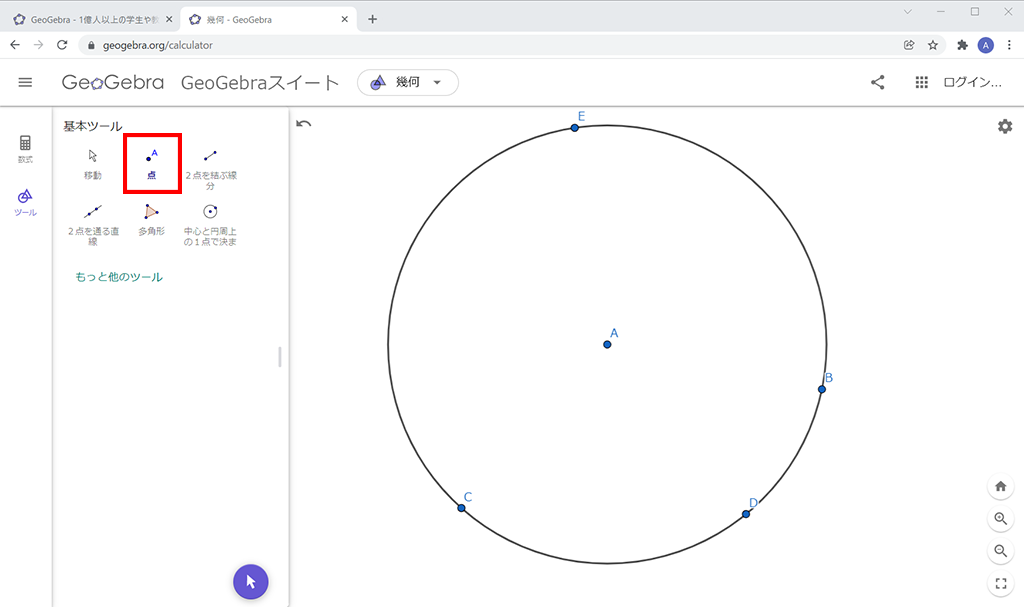
　「2点を結ぶ線分」を選択し、線分CEとDEを引きます。各々の2端点をクリックすると線分が引かれます。

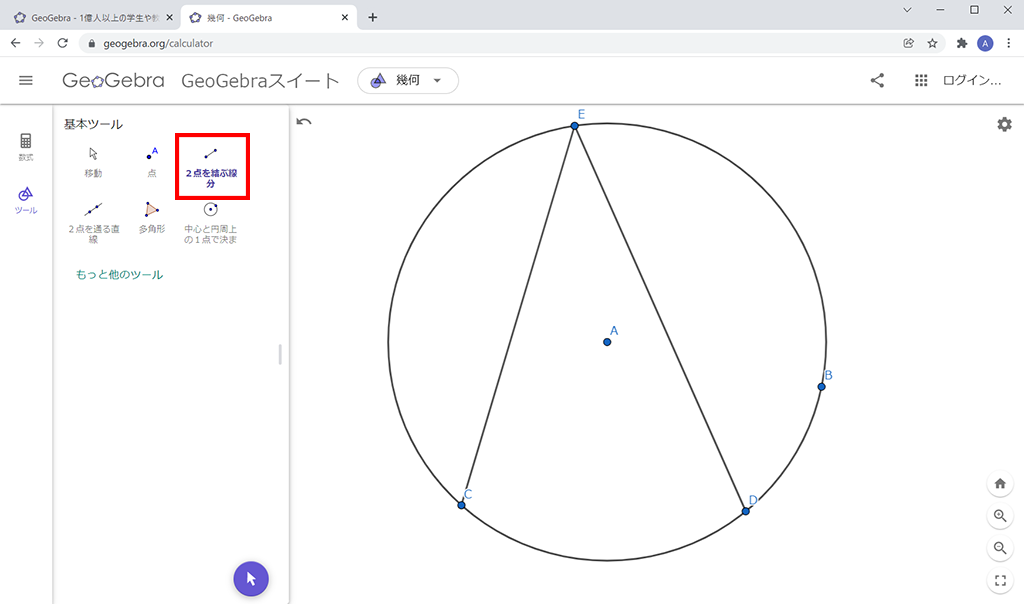
　「もっと他のツール」をクリックします。

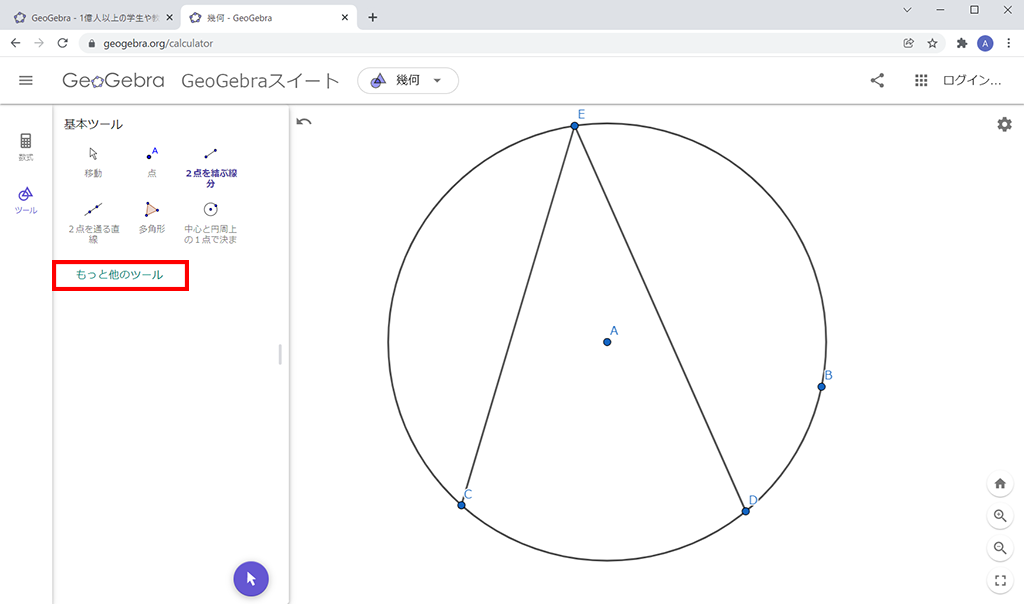
　「計測メニュー」内の「角度」を選択し、点C、E、Dの順にクリックすると、∠CEDの大きさが表示されます。

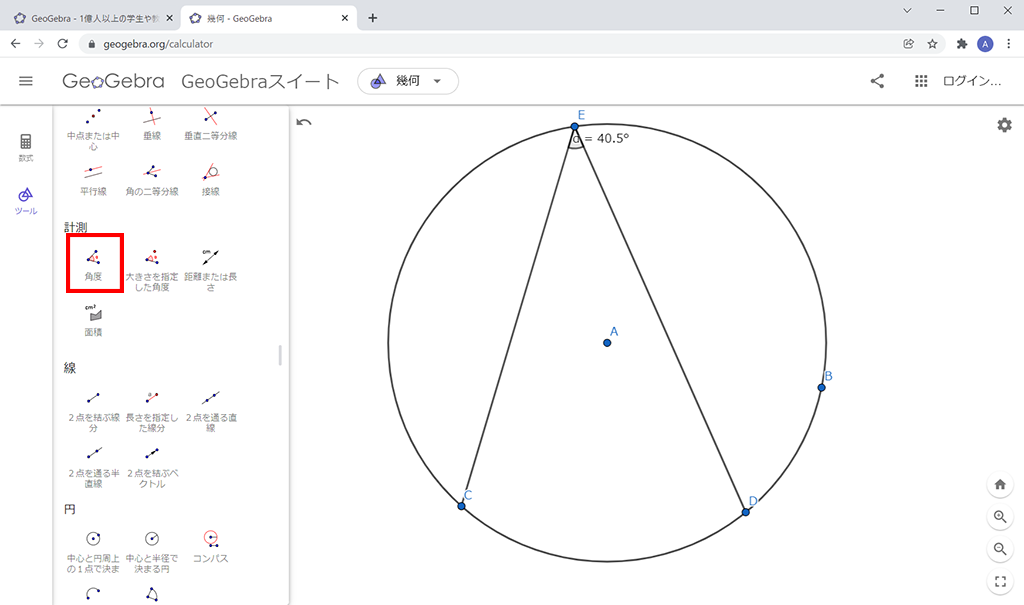
　「基本ツール」メニューの「移動」を選択し、点Dの位置を調整して、ちょうど∠CED=50°になるようにしました。この状態で点Eを動かせば、∠CEDの大きさは孤CD上では点Eの位置によらず常に50°であることがわかります。点を移動させるときは、メニューで「移動」を選択します。

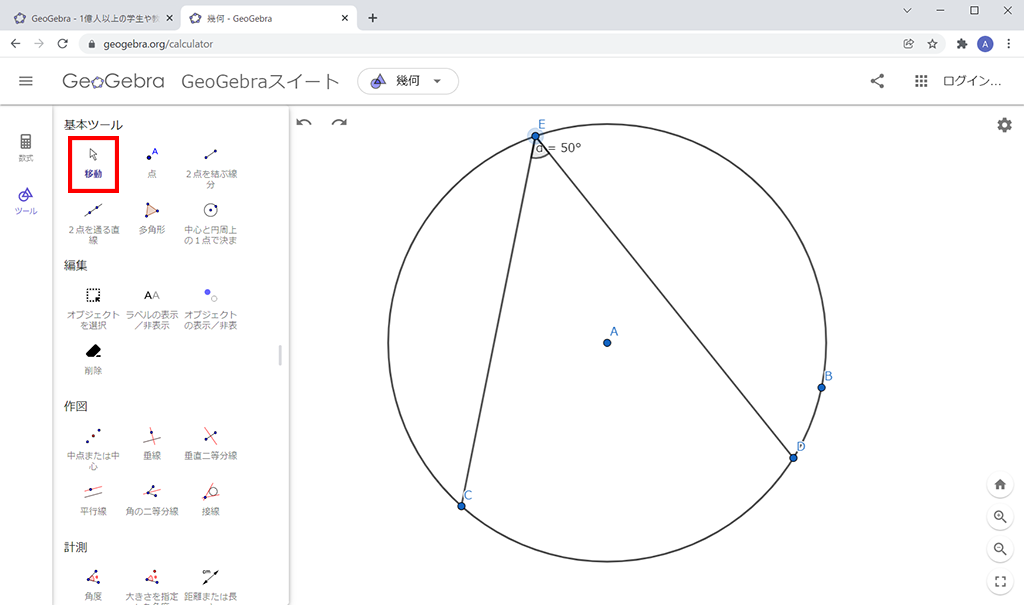
　点Eが下図のように劣弧CD上にあるときは、∠CED=230°になってしまいます。角の定義の仕方によるものですが、このままだと都合が悪いと思います。これを回避するために次の操作をします。

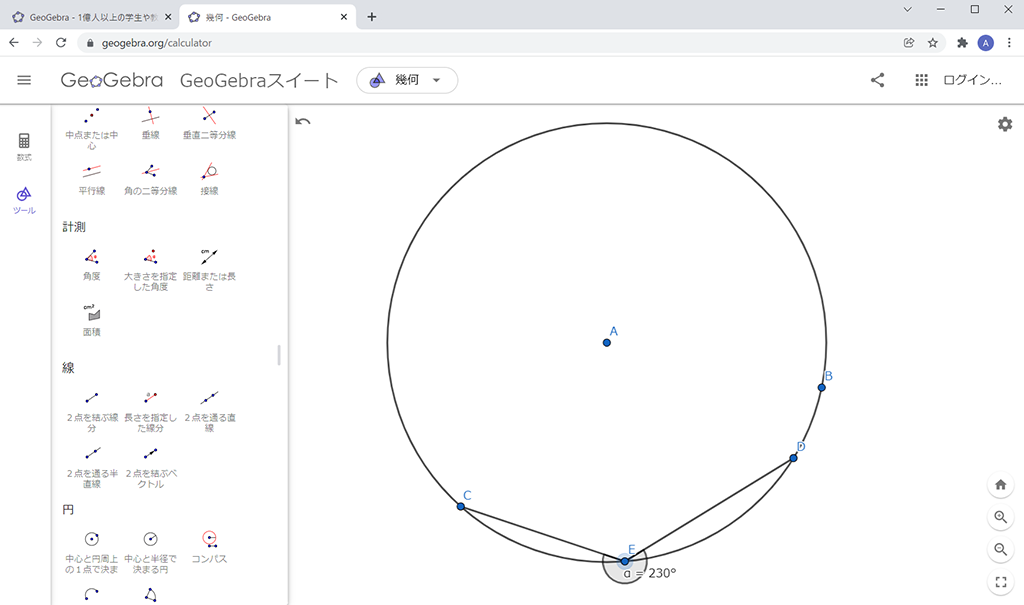
　∠CEDの上で右クリックをして表示されるメニューから、「角度」→「0°から180°」を選ぶと、130°と表示されるようになります。

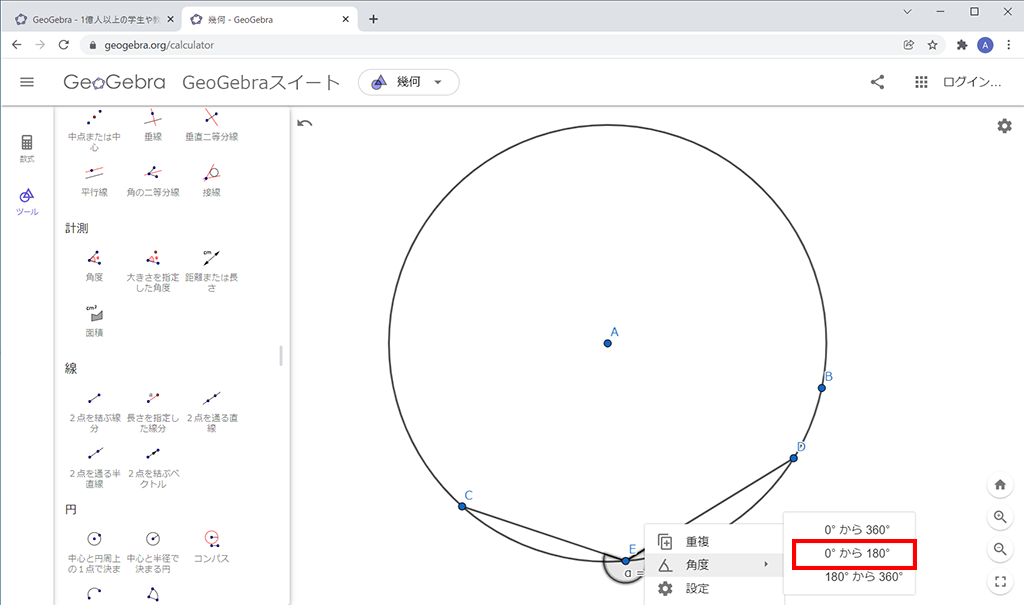
　円周上以外の点Fに対して、先ほどと同様に∠CFDを作成します。∠CFD=50°となる点Fの場所を探すのがこの授業のメインとなる活動ですので、これで準備ができました。左上の三線のボタン→「…形式でダウンロード」→「GeoGebraのデータファイル（.gbb）」を選択して、ファイルをダウンロードします。

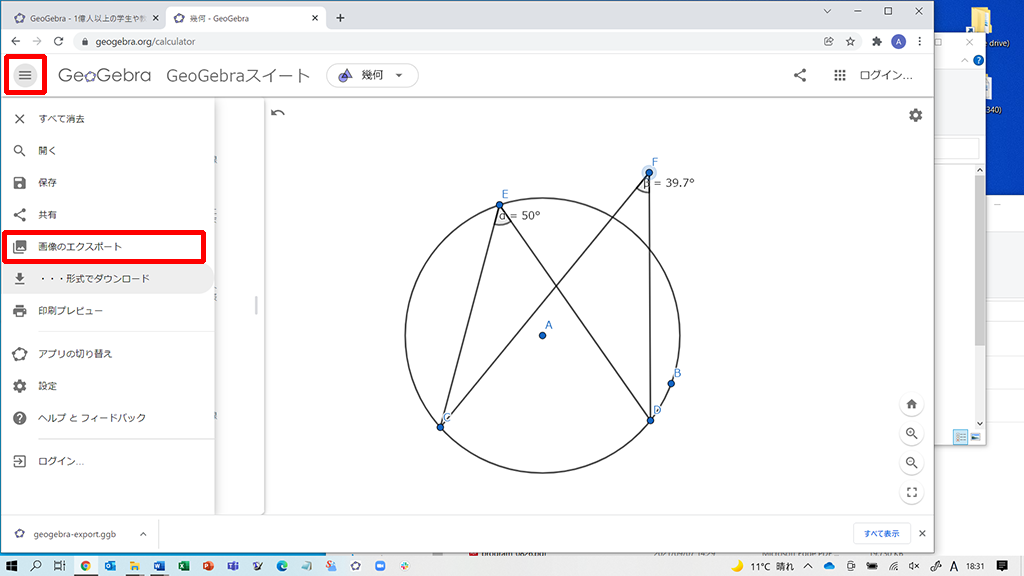
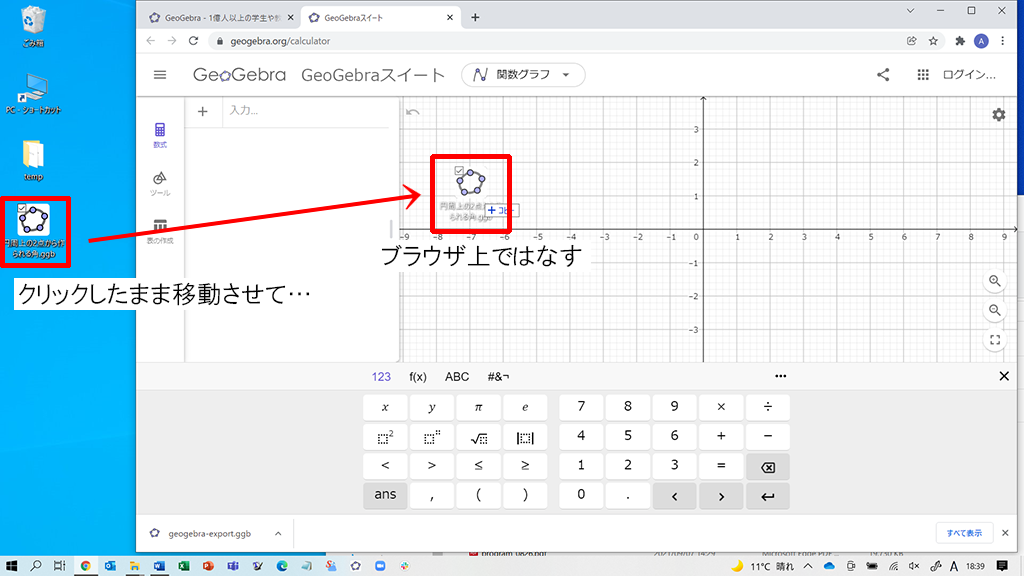
　ダウンロードしたファイルを生徒に配付します。このファイルを生徒のパソコンのデスクトップなどに配置して、GeoGebraを開いたブラウザにドラッグ＆ドロップすることで、先ほどの画面になります。

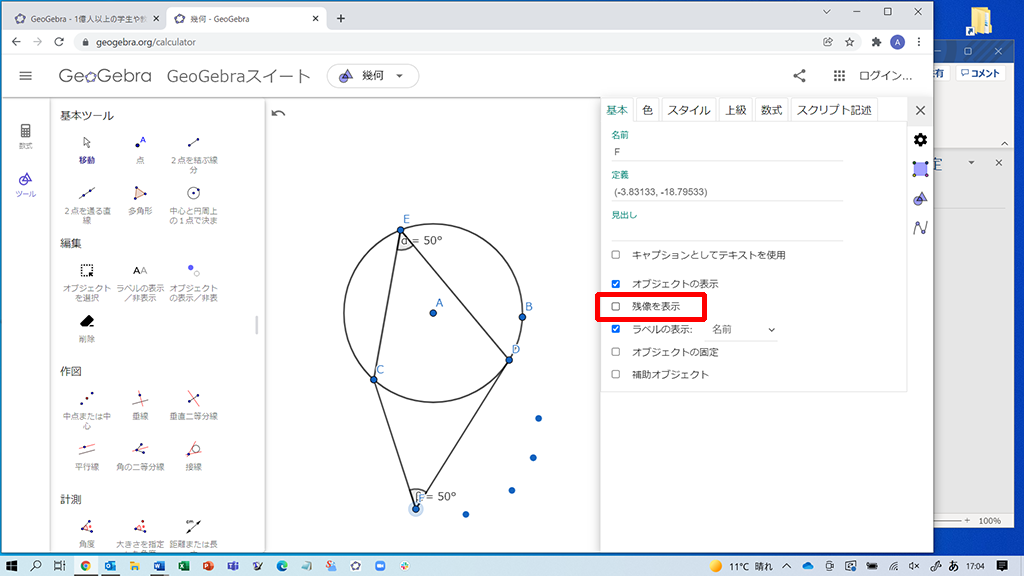
　∠CFD=50°となる点Fの場所は記録しておきたいと思うので、その方法を紹介します。∠CFD=50°となる場所で点Fを右クリックし「設定」を選択します。

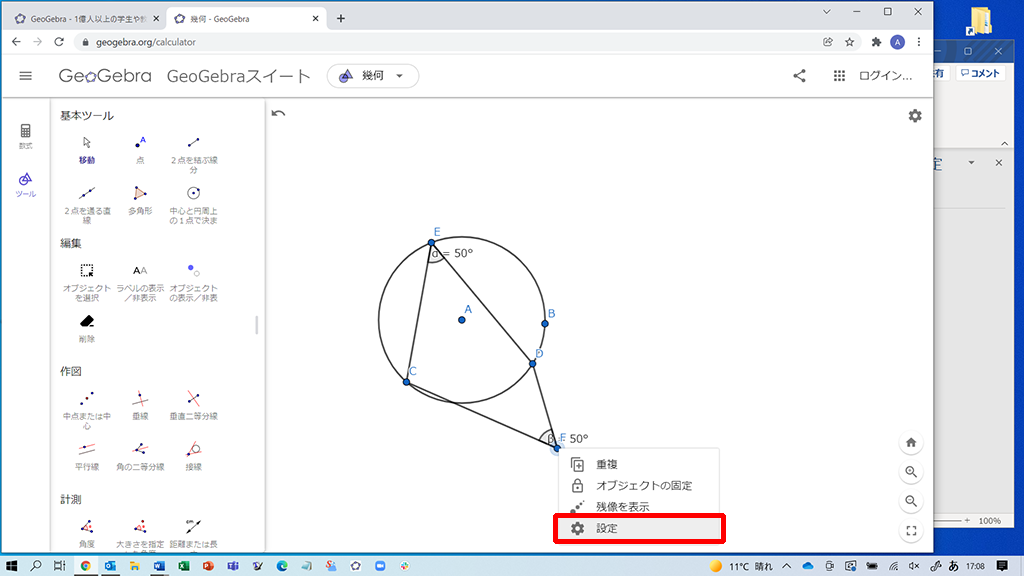
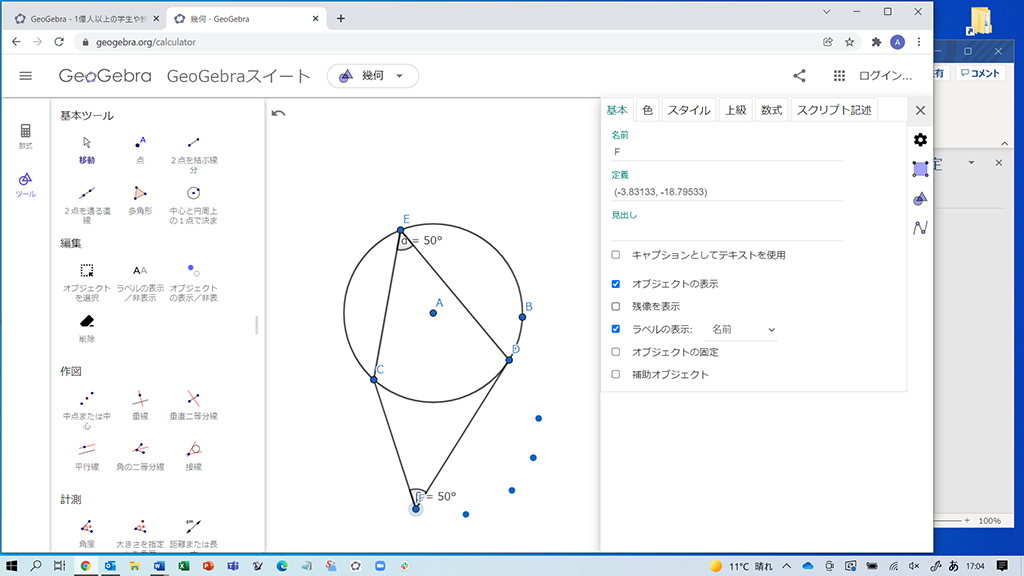
　画面右側の「残像を表示」のチェックボックスを一度クリックしてチェックを付け、再度クリックしてチェックを外すことによって点Fの残像が表示できます。∠CFD=50°となる場所を探す→残像を表示する、を繰り返すことで、点Fの集合が雪だるま型の図形の周囲になることを容易に確かめられます！

３　授業の展開

導入　「円周角の定理」の振り返り

　生徒用パソコンでGeoGebraのファイルを開き、次の画面を表示させて、生徒に点Eの位置をマウスで動かすように伝えます。点Eが上の図でCDに対して上側の弧CD上（優弧）にあるときは∠CED=50°、それ以外（劣弧）では∠CED=130°になることを確かめ、それが「円周角の定理」の意味だったことを振り返ります。

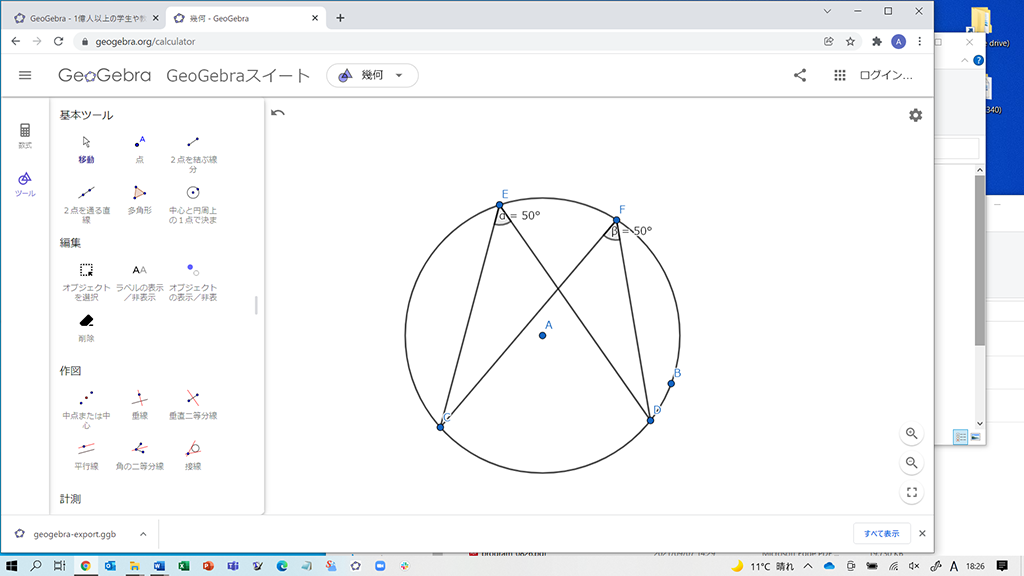
展開　円周上以外で∠CFD=50°となる点

　点Eが円周上になかったら、∠CEDの大きさはどうなるかを考えさせます。例えば、点Eが円周上にないとき、∠CEDは50°になると思うかを問いかけます。生徒は、おそらく50°にならないと思うはずです。そこで、「点Eが円周上にないとき∠CEDは50°にならない」という予想をGeoGebraを用いて検証します。画面上の点Fは円周上以外も動くようになっていることを伝え、マウスで点Fを動かして、∠CFDの大きさがどうなるかを調べさせます。

　（予想される生徒の反応）
　生徒A「50°にならないな」
　生徒B「円から遠ざかると小さくなるね」
　生徒C「0°まで小さくなるのかな？」
　生徒B「0°にはならないんじゃない？」
　生徒D「0°になる場所があったよ」
　生徒C「ほんと？どこ？あ、直線CDの上か。確かになるね。」
　生徒E「50°になる場所があったよ」

　円周上以外に∠CFDが50°になる場所の発見報告があったら、そのような場所が存在することを全体に共有して、それらの点をすべて集めると、どのような図形になるかを調べるように伝えます。ここで、点Fの残像を表示する機能を紹介します。

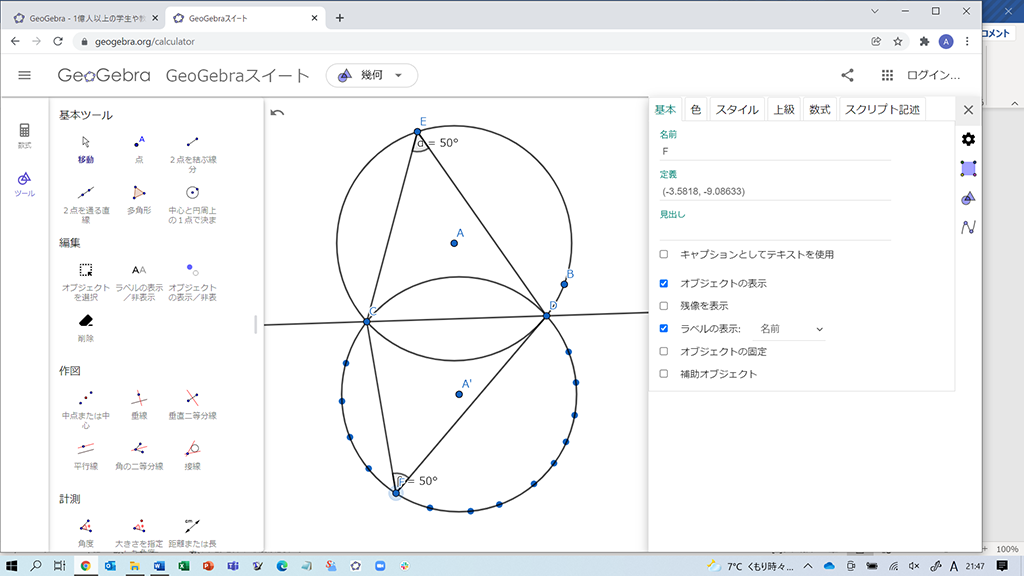
　∠CFD=50°になる点Fの集合はどのような図形になるかをことばで表現させます。雪だるま型であること、円の一部（劣弧の部分）は含まれないこと、上下の円が直線CDに関して対称になっていることなどを確かめます。また、次の図のように、「基本ツール」で直線CDを引き、直線CDに関して元の円と対称な円を図示することで、残像で表示した点がすべてその円上にあることを確かめることもできます。前時までにGeoGebraの基本的な操作を教えておけば、これらの操作を自分で行う生徒が現れると思います。

まとめ　「円周角の定理とその逆」

　最後に、∠CFD=50°となる点Fの位置は、雪だるま型の図形上以外にあったかどうかを問いかけます。「ない」と答えるはずです。このことから，本時は「∠CFD=50°ならば、点Fは必ず雪だるま型の図形上にある」ということを発見したと伝えます。まさにこの発見が「円周角の定理の逆」になっているということを確認して、授業を終了します。

　本時の経験によって教科書に書かれた「円周角の定理の逆」の意味が読みとれるようになると思います。次時は、その証明を行う想定です。

最後に

　今回の内容であれば、プリントと三角定規を用いて授業することもできました。しかし、GeoGebraを使うと、気になる1点の近くをひたすら拡大して調べたり、∠CFD=50°以外の場合、例えば、∠CFD=0°となる点Fの集合が示す図形を調べたりすることを、生徒が自分でやってみようと思う環境を提示することができます。詳しくは次回の記事で紹介します。