特集記事（小中学校）

横浜国立大学教育学部附属横浜中学校
教諭　八神純一先生

　現在、生徒一人に対して１台のPC端末が与えられ、多くの中学校でPC端末を活用した授業が展開されていると思われる。ここでは、私が中学１年生を対象に本年度実践したGeoGebraを活用した授業の中から２事例を紹介したい。

　GeoGebraとは、幾何、代数、表計算、グラフ、統計、解析を一つのパッケージにした教育用動的数学ソフトウェアで、ウェブサイト上にて無料で活用することができるものである(https://www.geogebra.org/)。教師がGeoGebraを用いて作成した教材(以下、「GeoGebra教材」)を生徒に配付すれば、生徒は各自のPC端末を用いて自由に操作することができる。その操作に応じて、結果を連続的に変化させることが可能なため、生徒は有能感や自己決定感を味わいながら、自ずと主体的に学習に取り組むことができるようになる。また、生徒は自らの操作によって得た発見に感動し、そのことを他者に伝えたくなるようだ。

　今回はGeoGebraの特性を生かして、「上級学年の学習内容に繋がる発見を多くの生徒が得ることができた事例」と「感動が伝播し、学びが深まった事例」を紹介する。

「図形」領域での活用

　まず、「GeoGebra教材」を用いることで、「上級学年の学習内容に繋がる発見を多くの生徒が得た事例」である。作図の学習で扱った「三角形の外心」の位置を考察させることで、「円周角」の学習内容に繋がる発見を多くの生徒が得ることができた。

　基本的な作図の活用場面として、いわゆる「銅鏡の復元」問題を扱った後、その流れで「三角形の外心と内心」の話をした。生徒一人ひとりが「三角形の外心と内心」をコンパスと定規を用いて求めたことを確認し、教師は教室内の大型スクリーンを用いてGeoGebra上で、その作図を再現した。

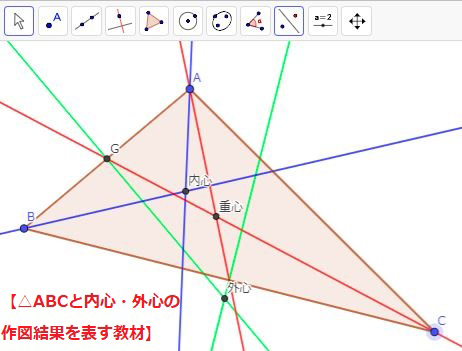
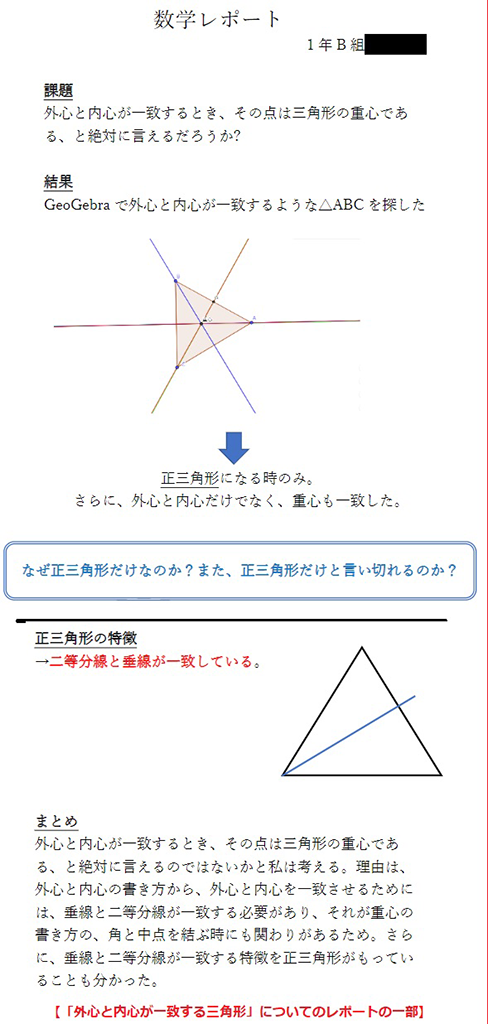
　その後、再現した「GeoGebra教材」を生徒に配付することで、今度は生徒一人ひとりが各自のPCで三角形を操作できるようになった。生徒が、三角形の各頂点を移動させれば、それに伴って「内心」や「外心」の位置も変化する。ここで生徒は、「内心」と「外心」を重ねようと各頂点を移動させた。「内心」と「外心」が重なるとき、正三角形になることを説明しようとする生徒とともに、三角形が「平べったい」(つまり「鈍角三角形」である)と「外心」が三角形の外側に出ることや、「外心」が辺上にあるときは直角三角形になることを発見した生徒もいた。これらは、中学校第３学年「円周角」の学習内容に繋がる発見である。

　このような発見は、ノートやプリント上に作図をしているだけでは得にくく、「GeoGebra教材」を活用することで得たのだと思われる。

「数と式」領域での活用

　次に「GeoGebra教材」を通して得た「感動が伝播し、学びが深まった事例」である。ある生徒が提出した「様々な不等式を作る過程における規則性について」のレポートが、「GeoGebra教材」の再操作を促し、学びを深めるきっかけになった。

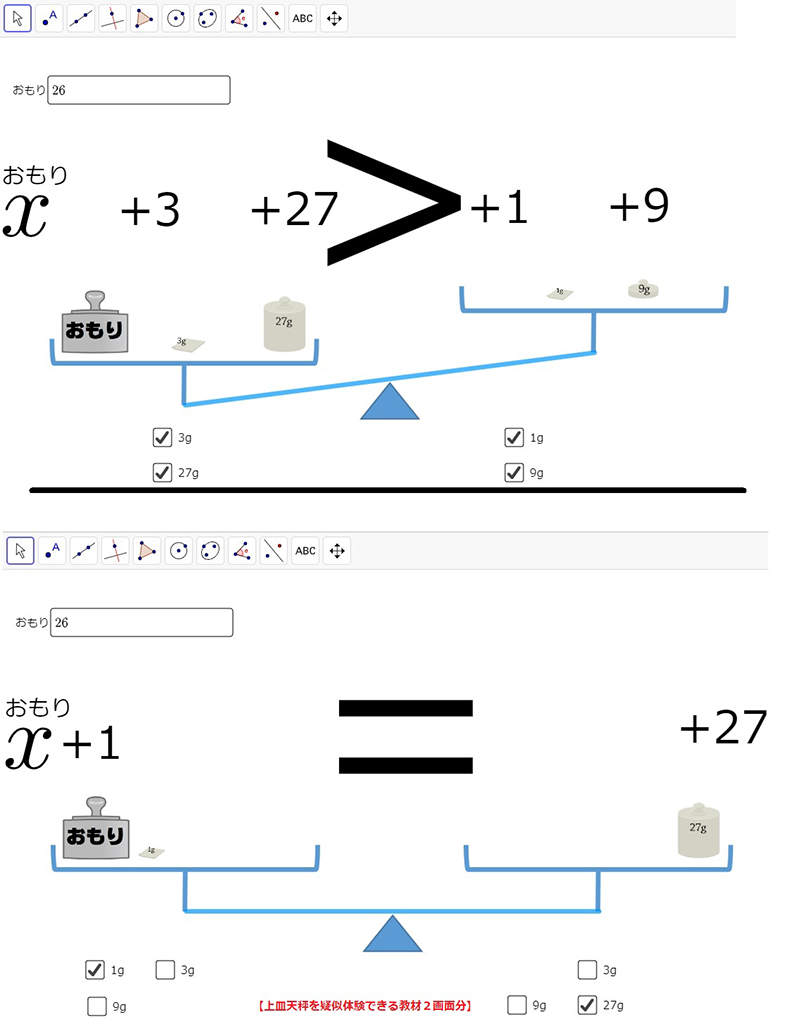
　最初に、生徒は「おもり」の重さとして、40以下の自然数を入力する。そして、その重さと釣り合うように、「１g」「３g」「９g」「27g」の４個の分銅から選択し、左右の皿に乗せる。左右の皿に乗った「おもり」や「分銅」の重さの合計に応じて、天秤の傾きは連続的に変化する。天秤が釣り合わなければ、画面に大きく不等号が映し出され、不等式が示される。天秤が釣り合うと、画面上に等号が映し出され、等式が示される。このようにして、「等号が相当関係を表す記号として用いられること」を、実感を伴って理解できるようにした。

　生徒は面白がって、「おもり」の重さとして様々な数値を入力して、ついに１gから40gまで全てのパターンを試した。その中で、それぞれの分銅を置く位置に法則を見出した生徒がレポートを提出した。そのレポートを共有したことがきっかけとなり、多くの生徒の探究心にまた火が付いた。「GeoGebra教材」を再度操作し、見出された分銅の法則を確認する生徒や、41g以上を量る際に必要な分銅を考える生徒が現れた。そして、分銅の重さが「３の累乗」であることに秘密があることを見出していった。

　人は自らの感動を他者に伝え、共有したくなる生きものである。GeoGebraはそのような「感動の共有」のきっかけを与えてくれる。学級の中で「感動」が共有され、その「感動」に対して数学的な価値付けがなされれば、生徒は俄然、学習にのめり込んでいく。

　今回は、「数と式」「図形」領域の事例を挙げたが、もちろん「関数」「データの活用」領域においてもGeoGebraは大活躍する。生徒一人に対して１台のPC端末が活用できる環境だからこそ、GeoGebraを用いて知的な「感動」が多く得られる授業を今後も展開していきたい。