今日の授業のひと工夫（小中学校）

4下p.73では、周りの長さが24\(\text{cm}\)の長方形や正方形で、面積が一番大きくなるのは縦の長さが何\(\text{cm}\)の時かを考えます。

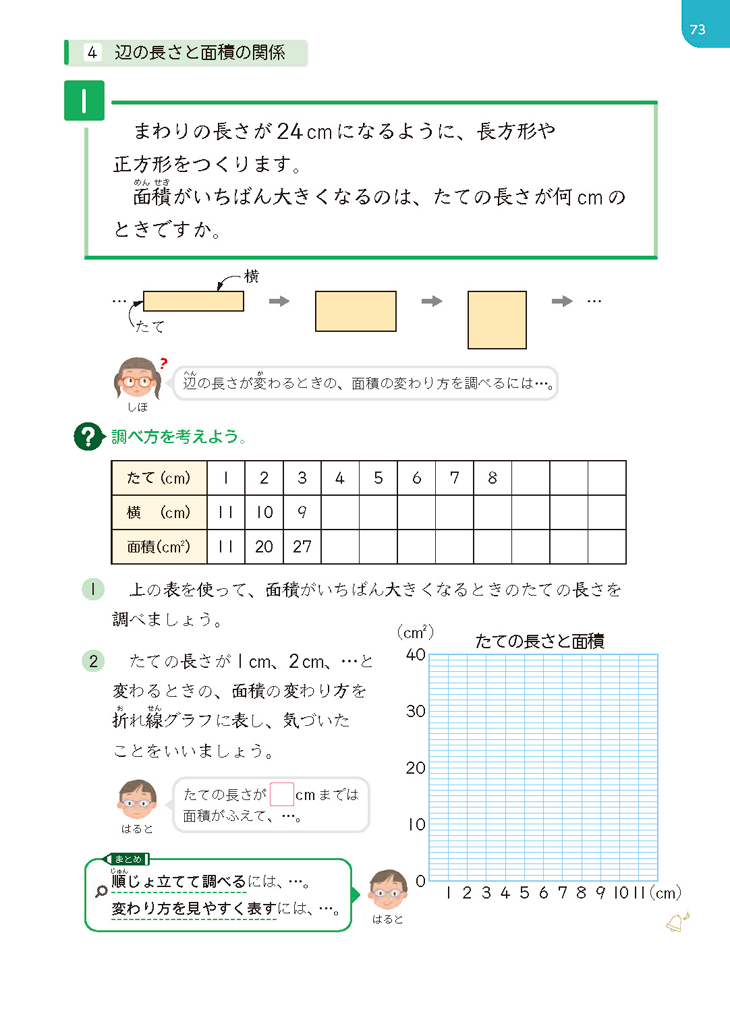
いろいろな形の図形が考えられますが、こんな時は表の出番ですね。第11単元「変わり方調べ」を想起させ、順序立てて表に整理していきます。表に表すと、「縦の長さが長くなると横の長さが短くなる」という伴って変わる関係であることが分かりやすくなります。また、縦の長さが6\(\text{cm}\)の時に、面積が最大になることも表から判断できます。

次に、縦の長さが変わる時の面積の変わり方を折れ線グラフに表します。下のような折れ線グラフになり、縦の長さが6\(\text{cm}\)までは面積が大きくなっていき、縦の長さが6\(\text{cm}\)より長くなると面積が小さくなっていくことが分かります。

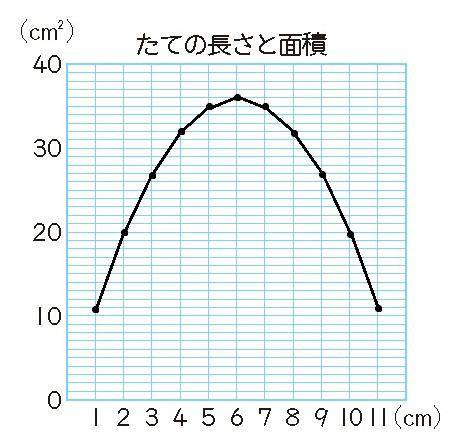
まとめでは、
①表に表すと、順序良く整理して調べることができる。
②折れ線グラフに表すと、変わり方がひと目で分かりやすい。
ということを確認し、4年で学習した「折れ線グラフと表」や「変わり方調べ」を活用したことを価値づけたいですね。