今日の授業のひと工夫（小中学校）

6年p.58では、分数のわり算を数直線の図を使って考える学習を通して、除法の意味を改めて見直します。
本時では、「\(\dfrac{7}{4}\) mの重さが \(\dfrac{2}{5}\) kg のホースがある」という場面から、何を1とするかが異なる2種類の問題を考えます。

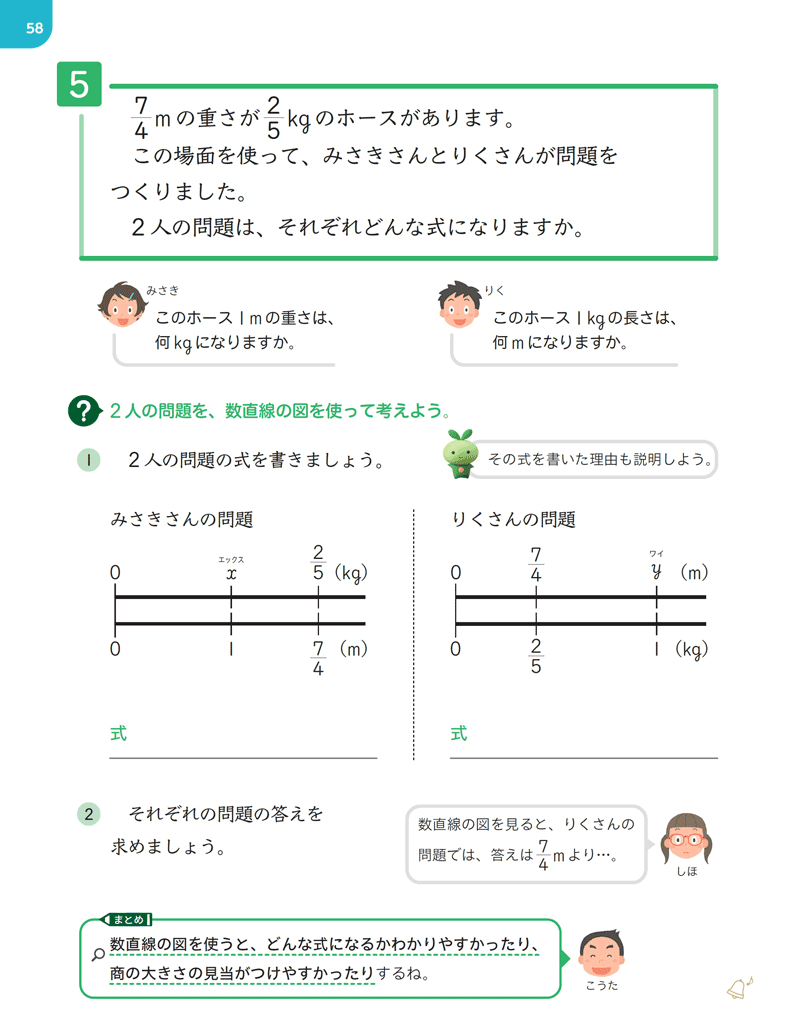
ここでは、いきなりかけ算の式になるかわり算の式になるかや、何を何でわればいいかということを問うのではなく、数直線の図に数量の関係を表す過程をていねいに扱い、1にあたるのは何か、基準量、比較量はそれぞれ何かを判断して立式させることがポイントです。
みさきさんの問題場面を例にしてみます。
数直線の図をかきます。（下図参照）

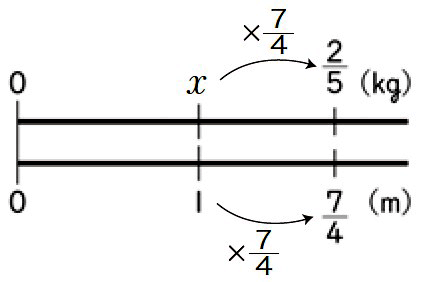
1から \(\dfrac{7}{4}\) になるには、\(\dfrac{7}{4}\) 倍なので、\(x\) を使ってまずは乗法の式に表します。
　式　\(x \times \dfrac{7}{4}= \dfrac{2}{5}\)
1にあたる大きさを求めるのはわり算なので、\(x\) を求める式は
　式　\(x=\dfrac{2}{5}\div \dfrac{7}{4}\)
というような流れで、児童には、まず乗法で数量の関係を表し、\(x\) を求めるために除法の式に表すことを説明させたいですね。

このとき、数直線の図をかくことが難しい児童がいる場合には、数直線の図のかき方を6年p.259に掲載していますので、数の大小や数の対応を確認しながらかき方を確認するとよいでしょう。また、教科書では、数直線の図をかくとき、単位量を意識できるようにするために、1にあたる数量を下にかくようにしていますので、かき方を統一し、数量の関係を共有しやすいようにしておくことも合わせて確認しておきましょう。
まとめでは、数量の関係に着目し、その関係を数直線の図を用いて整理すると、数量の関係をとらえやすくなり、立式しやすいことを価値づけましょう。