今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【3年1章(自由研究)】パスカルの三角形

「新しい数学」3年巻末p.232「パスカルの三角形」では、数の並びと多項式の関係や数の並び方の規則性を見つける活動をします。

❶で、\((a+b)^3\) を展開した結果を、係数を明らかにして書くと次のようになります。
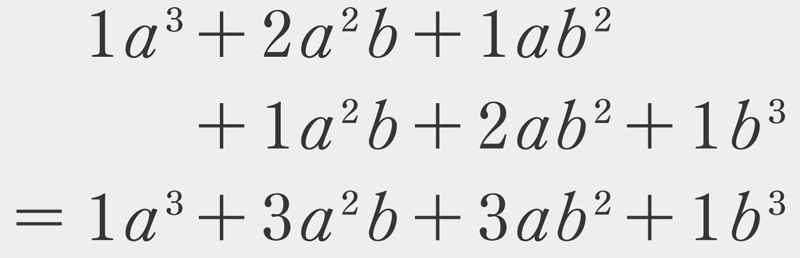
よって、\((a+b)^3\) を展開した式において、両端の1以外の係数は、\((a+b)^2\)を展開した式のとなり合う係数1と2、2と1のそれぞれの和として得られることがわかりますね。同様に考えると、\((a+b)^4\) の場合では、\((a+b)^3\) を展開した式のとなり合う係数1と3、3と3、3と1のそれぞれの和として得られることが予想できます。

\((a+b)^n\) を展開した式の係数を図のように並べたものが、このパスカルの三角形ですが、係数を一般化したものが高校で学習する「二項定理」です。
二項定理もここでの活動と同じように小さい指数の場合で考えて、係数の規則性を一般化することができます。
例えば、\((a+b)^4\) は4つの因数 \((a+b)\) の積です。展開した式のうち、\(a^3b\) の項は、4つの因数から1つを選んで \(b\) を取り出し、残り3つの因数から \(a\) を取り出してかけ合わせることによって得られます。すなわち、4つの因数から1つを選ぶ選び方の数だけ \(a^3b\) の項ができるので、\(a^3b\) の係数は \({}_4\mathrm{C}_1\) となります。
同様に考えると、\((a+b)^4\) を展開した式のすべての項
\(a^4\) 、\(a^3b\) 、\(a^2b^2\) 、\(ab^3\) 、\(b^4\)
の係数はそれぞれ
\({}_4\mathrm{C}_0\) 、\({}_4\mathrm{C}_1\) 、\({}_4\mathrm{C}_2\) 、\({}_4\mathrm{C}_3\) 、\({}_4\mathrm{C}_4\)
です。一般に、次の二項定理が成り立ちます。
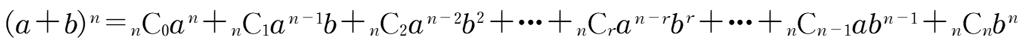
その他のコンテンツ
