今日の授業のひと工夫（小中学校）

「新編 新しい数学」2年巻末p.232「17段目のふしぎ」では、手順に従って1段目から数を書いたとき、17段目に入る数がどんな数になるのか調べ、文字を使ってそのきまりを見つけていきます。

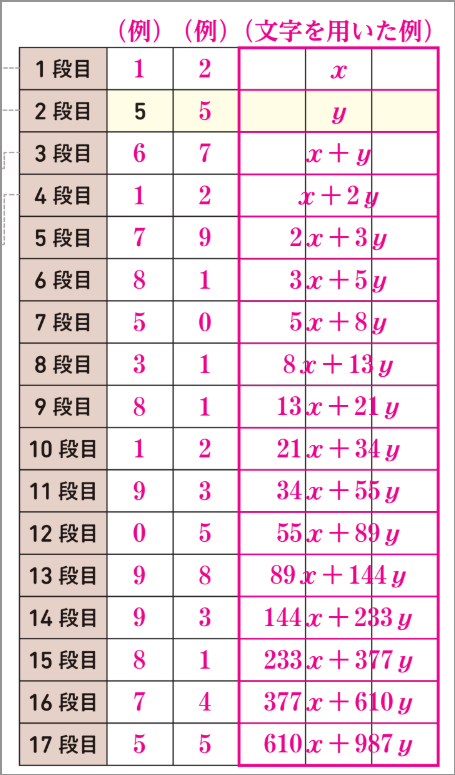
上の表の（文字を用いた例）で、例えば、8段目の \(8x+13y\) の一の位は、一の位に影響しない \(10y\) をひいた \(8x+3y\) の一の位と一致します。同様に考えると、16段目の一の位は、\(7x\) の一の位と一致し、17段目の一の位は、\(7y\) の一の位と一致しますね。このことから、16段目は1段目だけで、17段目は2段目だけで決まることがわかります。

「17段目のふしぎ」は、この性質を利用し、1段目を変えても2段目が5であれば17段目も5であること（5の7倍の一の位の数であること）に気づき、さらに、2段目と17段目の関係を帰納的に見つけ、文字を用いて考えます。①、②で、具体的な操作を通して、帰納的に性質を発見する楽しさを味わい、さらに、文字を用いることで構造が見えてくることを体験したいところです。

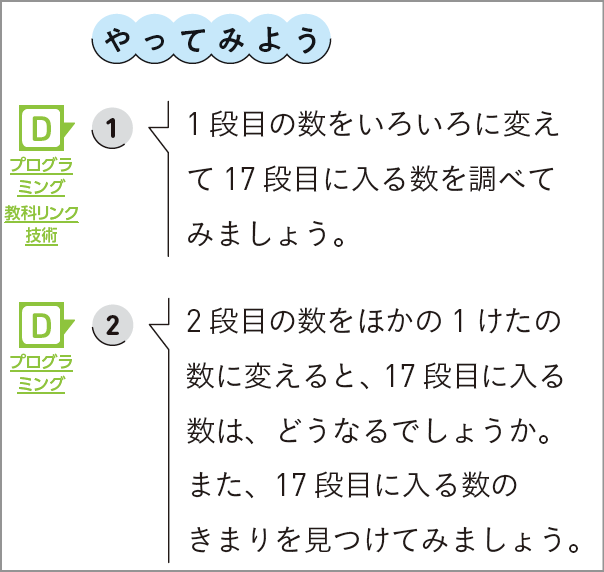
①の活動のなかで、2段目を5にすると1段目に関わらず17段目も5になることに気づき、その後、②の「2段目の数を変えると、17段目に入る数は、どうなるか。」という疑問が生徒から自然と出てくることを期待したいですね。

また、②について仮説を立てると、多くの生徒は一致すると考えるでしょう。そのうえで各自が調べると、この仮説が正しくないことがすぐにわかります。このように「仮説を立て、実際に検証する」という目的意識をもって活動をしたいところですね。

様々な見方をするなかで、17段目は2段目の7倍の一の位の数ということに気づき、文字を用いて説明できるようになりたいですね。文字を用いて説明する際には、はじめはそのまま計算し、最後に一の位について考えるように指導したいところです。

また、各段の値を求める計算は、③に示したアルゴリズムの繰り返しです。

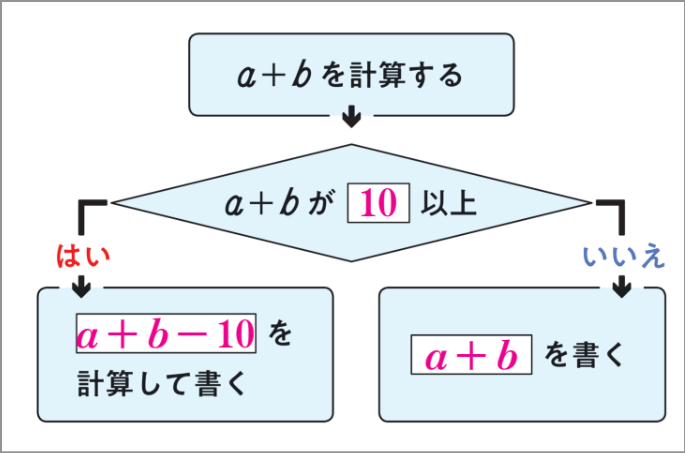
このように入力された値が、一定の手順に従って出力される構造はプログラミングと関係があることを生徒に意識させたいところです。QRコンテンツでは、スクラッチを用いて17段目のふしぎを確認できるシミュレーションを用意しています。ソースコードを確認してアルゴリズムにも触れることで、より一層理解を深めていきたいですね。

QRコンテンツはこちら

＞17段目の不思議

＞17段目の不思議（2段目を変えてみよう）

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。