今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【1年7章】階級の幅をいろいろと変えてヒストグラム…

1年7章では、サッカーチームの状態を分析するために、1500m走の記録を度数分布表やヒストグラムに整理して、分布の特徴を読みとり、判断する力を身につけることをねらいとしています。

p.226❾では、階級の幅を変えてヒストグラムをつくり、p.225でつくった階級の幅10秒のときと同じ特徴がいえるか読みとります。
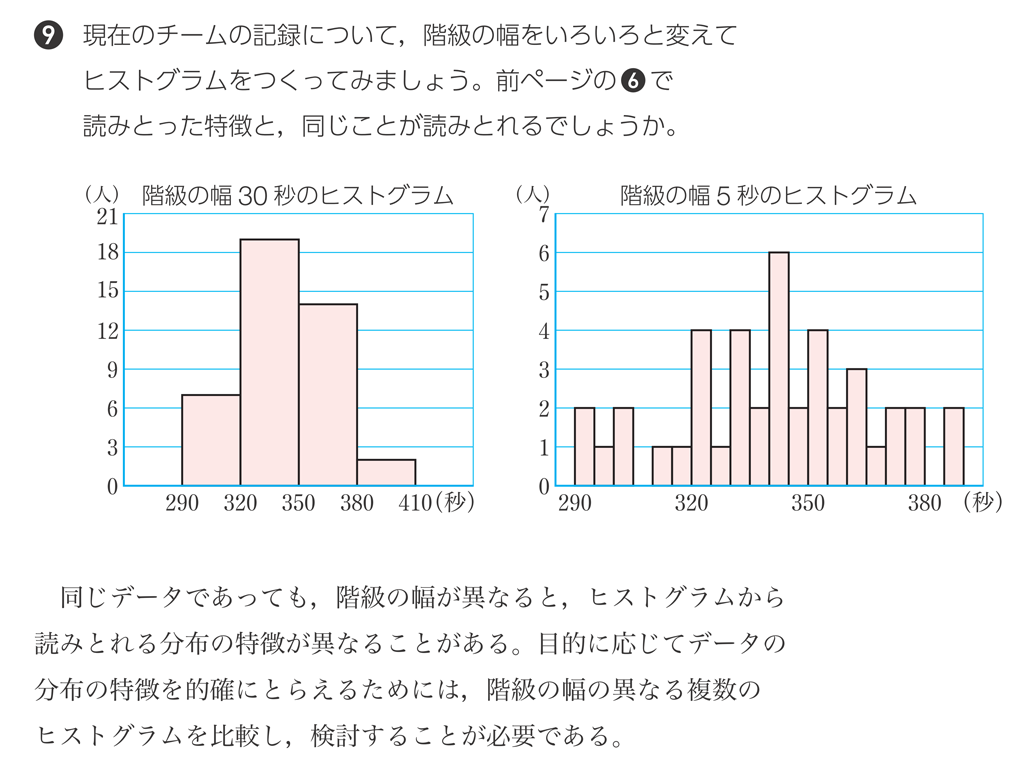
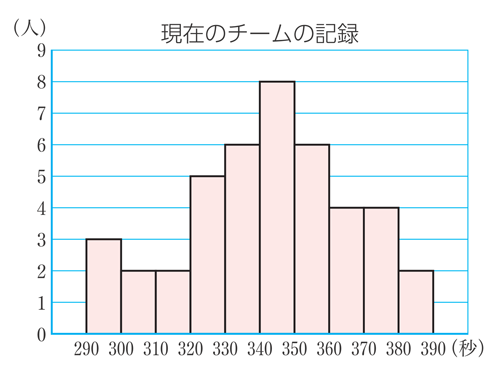
(階級の幅10秒のヒストグラム)
このように階級の選び方によってヒストグラムの形状が変わるため受け手に異なる印象を与える可能性がありますので、階級の選び方が重要であることを伝えたいところです。しかし、階級の選び方には明確なきまりがあるわけではないので、分布の特徴がより見やすくなるように階級を選ぶ必要があります。そのためには、幅を動かしてみて、複数のヒストグラムを比較、検討する必要があることを、この❾を通して伝えたいですね。
一般には、データの集中(中心傾向)が読みとれる、つまりヒストグラムに山が形成されるように階級を選ぶことが考えられます。幅が小さすぎると歯抜けのような形になり山が形成されず、また幅が大きすぎると長方形がいくつかあるだけで山とは捉えにくくなり、いずれも分布の特徴が読みとれません。階級数や幅を決める一つの方法として、スタージェスの公式「階級数を \(k\) 、観測値の個数を \(n\) で表すと、\(k\fallingdotseq1+\log_{2}n\)」があります。 授業で取り上げる必要はありませんが、オリジナル問題を作成するときのためにも、知っておきたいですね。
その他のコンテンツ
