今日の授業のひと工夫（小中学校）

1年6章p.220の数学のまどでは、「球の体積と表面積の関係」について考えます。ここでは、球の体積がわかっているときに、その表面積を求める方法を示しています。

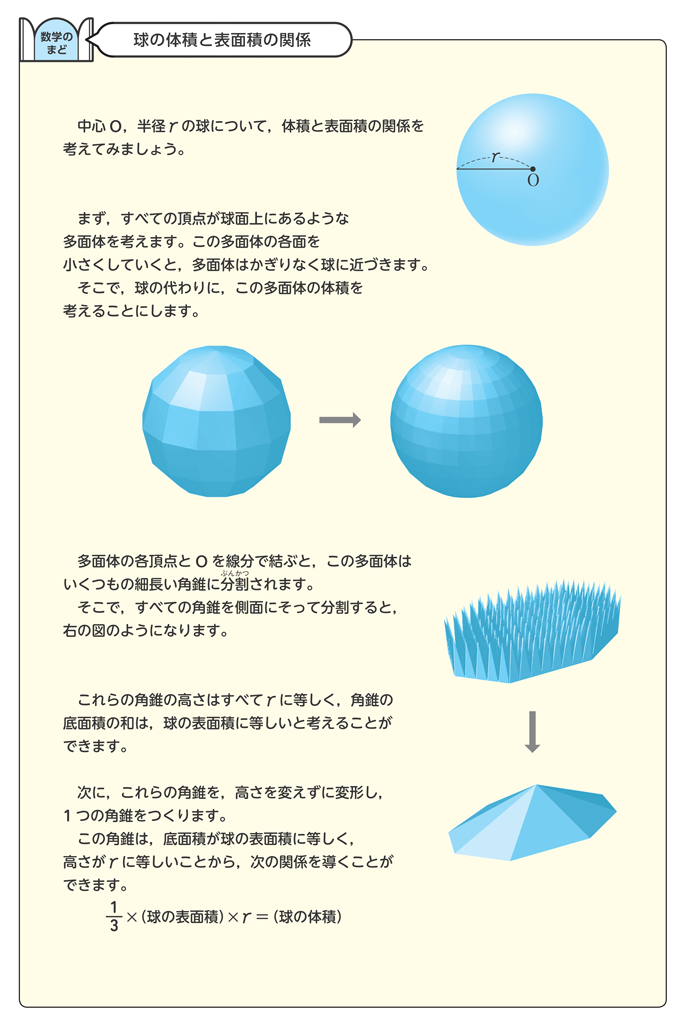
実際に模型を作ったりすることは難しいので、教科書にある図を見ながら、イメージを捉え、結論を納得させるようにします。

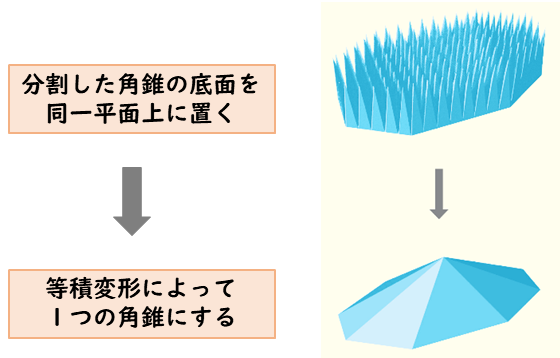
また、文字式を用いる場合は、例えば次のようにします。

球の半径を \(r\) とし、おのおのの角錐の底面積を \(S_1，S_2，S_3，\cdots\) 、高さを \(h_1，h_2，h_3，\cdots\) とすると、多面体の体積は

(多面体の体積) \(=\dfrac{1}{3}S_{1}h_{1}+\dfrac{1}{3}S_{2}h_{2}+\dfrac{1}{3}S_{3}h_{3}+\cdots\)　　……①

で求められます。多面体の各面を小さくして角錐の個数を大きくしていくと、\(h_1，h_2，h_3，\cdots\) はいずれも \(r\) に近づくから、①より

\(\dfrac{1}{3}(S_{1}+S_{2}+S_{3}+\cdots)r\)

となり、\((S_{1}+S_{2}+S_{3}+\cdots)\) は球の表面積に近づくから

(球の体積) \(=\dfrac{1}{3}\times\) (球の表面積) \(\times r\)

となります。球の体積は \(\dfrac{4}{3}\pi r^3\) であるから、この関係式から球の表面積は \(4\pi r^2\) で求められることがわかりますね。