今日の授業のひと工夫（小中学校）

3年7章2節では、三平方の定理を利用して、具体的な場面で求めたい長さを求める方法を考えられることをねらいとしています。

p.193の導入では、三平方の定理を活用できる具体的な場面として、イルミネーションのコードの長さを求めることを課題としました。奥行と高さはわかるが斜めの長さがわからない、そしてその長さを求めることに価値がある場面です。

この図では、この課題を解決するのに必要な長さは図示されていません。生徒と議論をしながら、イルミネーションのコードの長さを求めるには、どこの長さが必要なのか、そしてそれをどのように活用すればよいかなどを生徒から引き出し、円錐の半径と高さで切り出される直角三角形に着目できるようにしたいところです。

ここでは、イルミネーション全体を円錐ととらえることで、花だんの半径とモニュメントの高さ、そして母線にあたるコードの長さを用いる直角三角形を見いだすことができますね。

実際のコードは多少たるんでいますが、それを直線とみなすことで、数学の問題として捉えることができます。また、コードの長さを求める必然性にも触れておきたいところです。例えば、具体的な長さがある程度の精度でわからないと、イルミネーションのコードを購入できないことや、コードの長さを実測しにくいことなどに触れると長さを求める必然性が生徒にも実感できるでしょう。

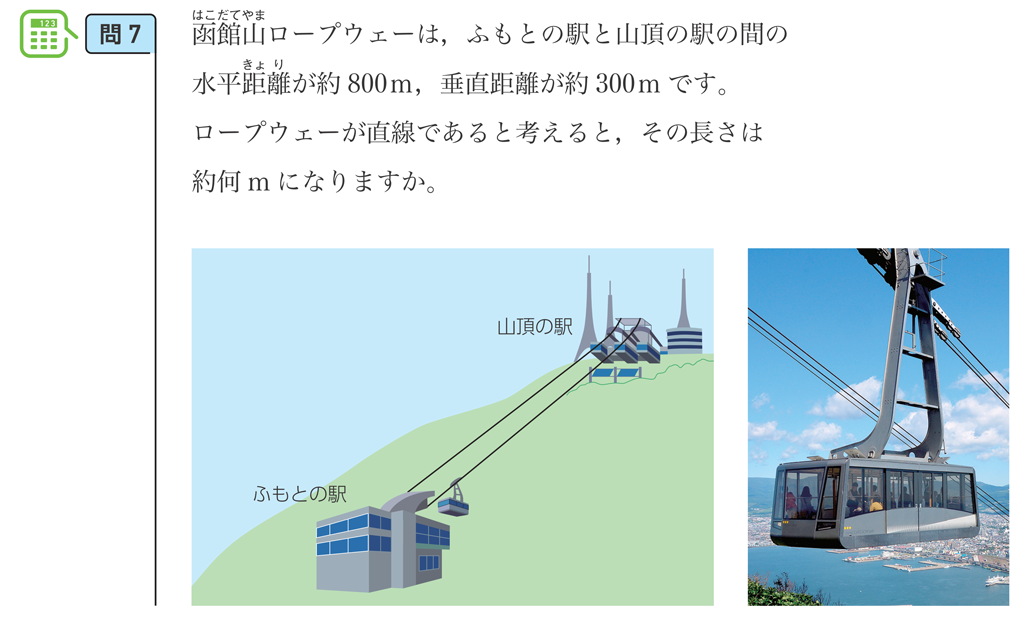
p.196問7では、問題中にデータがすべて与えられ、ロープウェーも直線とみなすことが明示されていますが、授業では p.193のイルミネーションの問題と同様、どの長さが必要なのか、どの情報を単純化して「何をどんな図形にみなす」のかなどを、生徒との議論のなかでていねいに進めていきたいところです。

例えば、地図を用意したうえで「函館山のロープウェーの長さを求められるか」と問い、それを求めるためにはどのようなデータが必要かを考えていきます。このような議論のなかで、「ロープウェーは途中で傾きが変わっていたり、たわんでいたりするが、どうしたらよいか」ということが問題となり、直線とみなしてよいかも検討されることでしょう。

このような流れのなかで明らかになったことと、これからの学習で明らかにしていきたいこと（今回であれば曲線の長さについての学習など）が整理され、主体的に学びに向かう力も育まれることが期待できます。