今日の授業のひと工夫（小中学校）

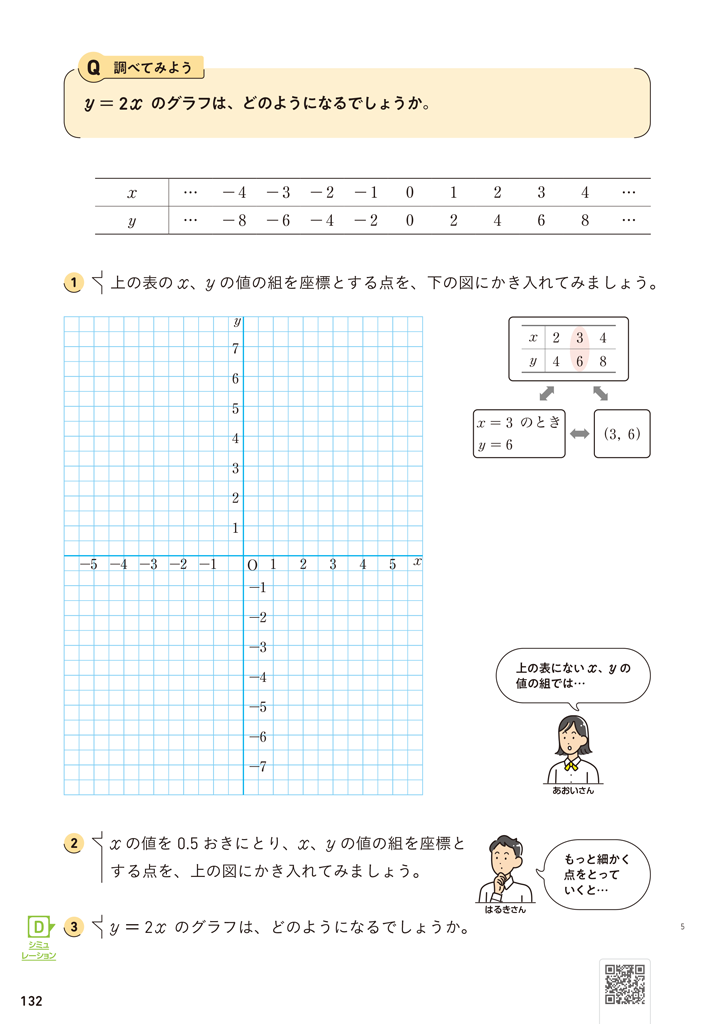
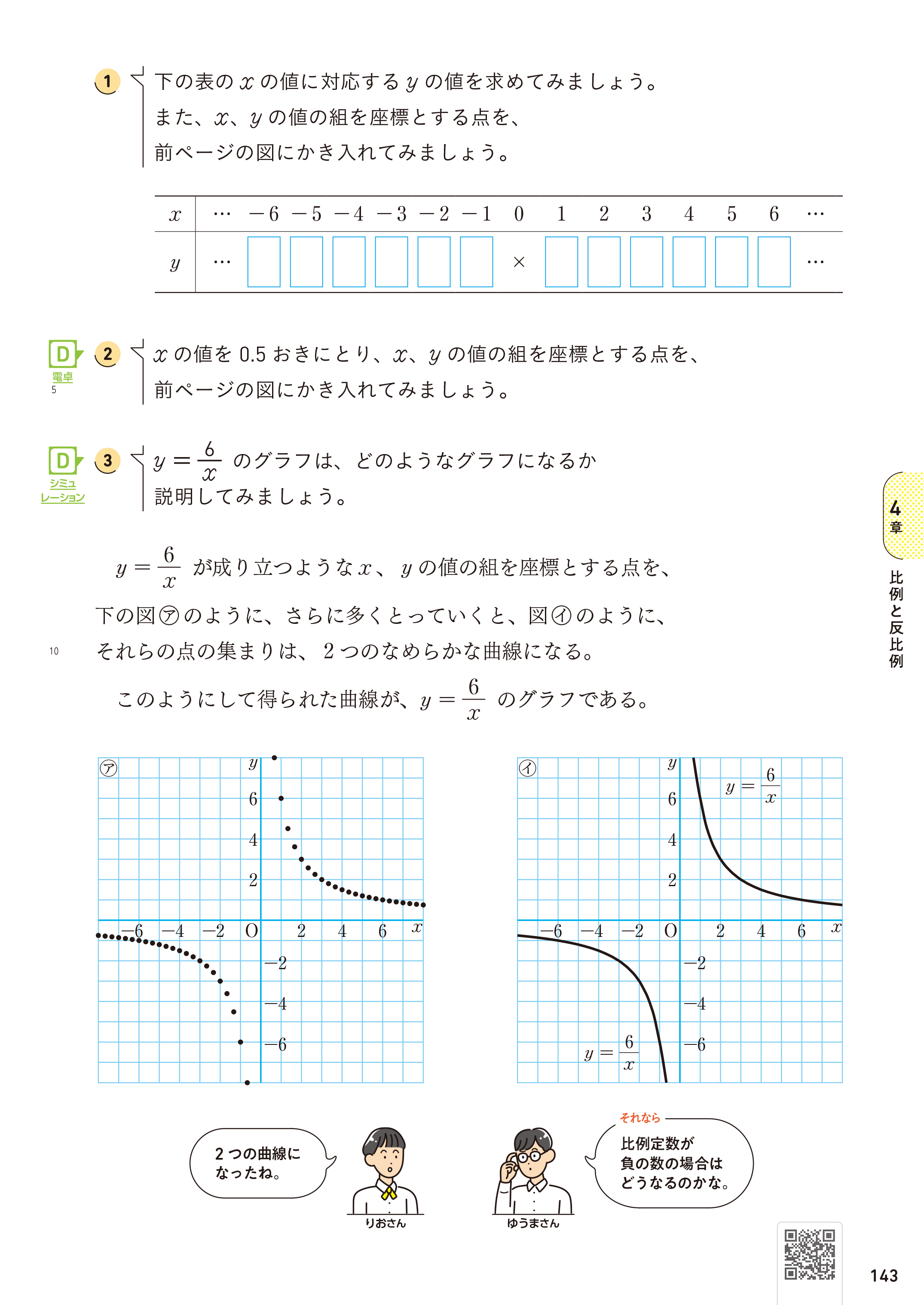
「新編 新しい数学」1年4章p.132、143では、\(x\) の変域を負の数にひろげたときの比例のグラフと反比例のグラフをかいていきます。どちらのグラフも点の集合であることを理解させたいところです。

小学校では、\(x \geqq 0\) 、\(y \geqq 0\) の範囲の比例のグラフを学び、折れ線としてグラフを捉えてきましたが、中学校では、グラフを点の集合として捉えていきます。p.132Qでは、\(y=2x\) の形の式が比例の関係を規定しているということを意識させたいところです。

あおいさんとはるきさんの2つの吹き出しと②は、グラフを点の集合として理解させることを意図しています。小学校で比例のグラフは直線であることを学習しているため、①の時点で直線をひく生徒がいるかもしれませんね。その際は、「表にない \(x\) 、\(y\) の値の組も本当に直線上にあるのか」と投げかけ、 ②の活動につなげるようにしましょう。そして、さらに細かく点をとることを促し、作業を通して点の集合としてグラフを理解させるようにしたいですね。

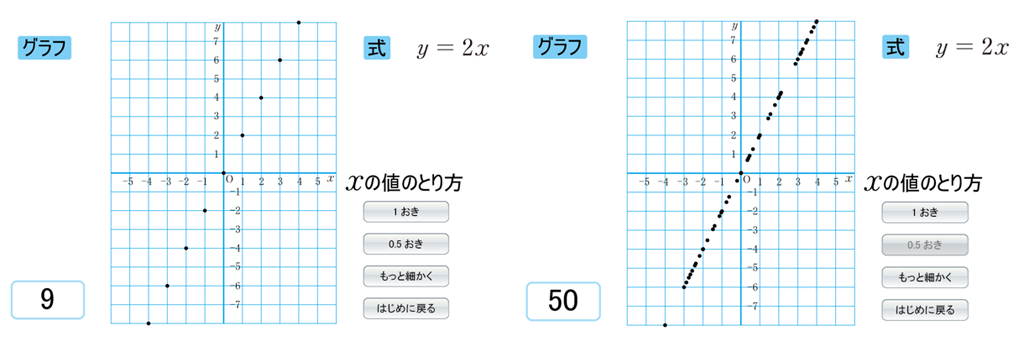
QRコンテンツでは、\(x\) の値のとり方を1おき、0.5おきと簡単に変えて点をとることができるうえに、「もっと細かく」でランダムに値を変えて点をとることができるので、それらの点の集まりが1つの直線になることを視覚的に理解できるようになっています。

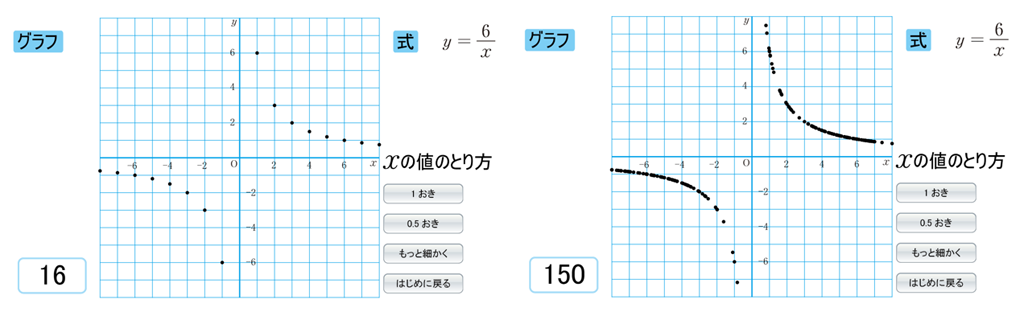
比例のグラフは直線であるため、かかれたグラフは、いくつかの点をとって、それらを線分で結んだものと変わりがないですよね。それに対して、反比例のグラフは曲線であるから、グラフが点の集合であることを強調するのに適当な題材です。したがって、できるだけ細かく点をとって、点の集合が曲線であるということを実感として理解させたいところです。

例えば、\(x=1.25\) のときの \(y\) の値 \((y=4.8)\)を求め、点(1,6)と点(1.5,4)を結んだ線分上にあるかを調べます。そのうえで、より細かく点をとっていくと曲線になることを、QRコンテンツを使って確認し、グラフが点の集合であることを意識させたいところです。

p.132Qでは、比例の式 \(y=2x\) から、\(x\) と \(y\) の値を計算して表ができている点に触れ、②で \(x\) の値を0.5おきにとった場合も、同じように式から \(y\) の値が求められるという点に注意したいですね。

関連記事はこちら

＞【思考を見せる板書例】1年4章：比例の表やグラフから式を求める方法を考えてみよう

QRコンテンツはこちら

＞比例のグラフを調べよう

＞反比例のグラフを調べよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。