今日の授業のひと工夫（小中学校）

「新編 新しい数学」2年3章p.69では、これまでに学んだ1次関数を表、式、グラフの関係にまとめます。1次関数の特徴のなかでも、特に、変化の割合（グラフの傾き）とグラフの切片について、表と式とグラフの三者を相互に関連づけて理解することをねらいとしています。

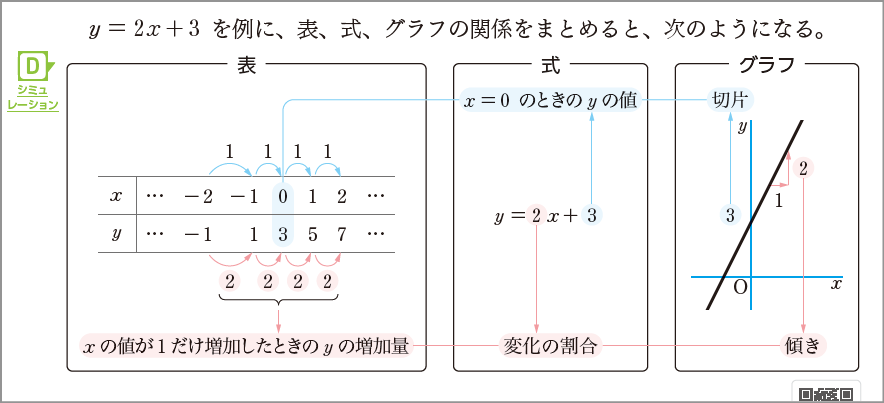
教科書では \(y=2x+3\) についてまとめていますが、ほかにも、例えば \(y=-2x-1\)について、同じように、教科書を参考にしながらまとめてもよいですね。1次関数の特徴を表、式、グラフを関連づけてさらに理解することが期待できます。

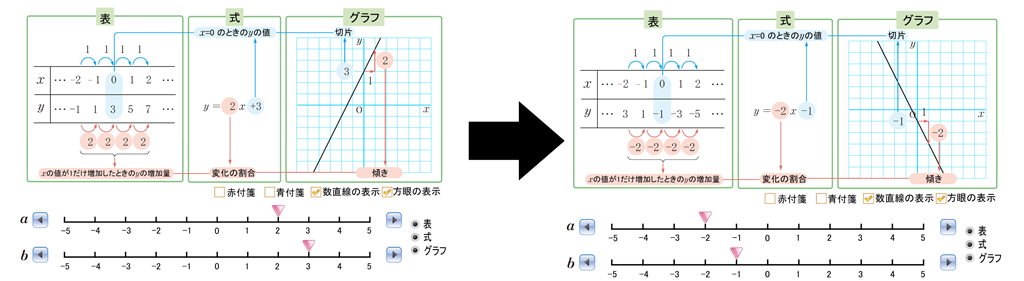
QRコンテンツを使えば、\(a\)、\(b\) の値を変化させたときの、表、式、グラフをまとめて表示することができます。表、式、グラフが連動して変化するので、それぞれの関連が分かりやすくなります。また、付箋機能で数値をかくして特徴を生徒と一緒に確認するのもよいですね。

QRコンテンツはこちら

＞表・式・グラフの関係を調べよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。

関連記事はこちら

＞授業で活用！QRコンテンツおすすめ使い方動画！③ 2年p.69「表・式・グラフの関係を調べよう」