今日の授業のひと工夫（小中学校）

「新しい数学」2年1章の導入では、陸上トラックのセパレートコースのスタート地点の差を調べます。

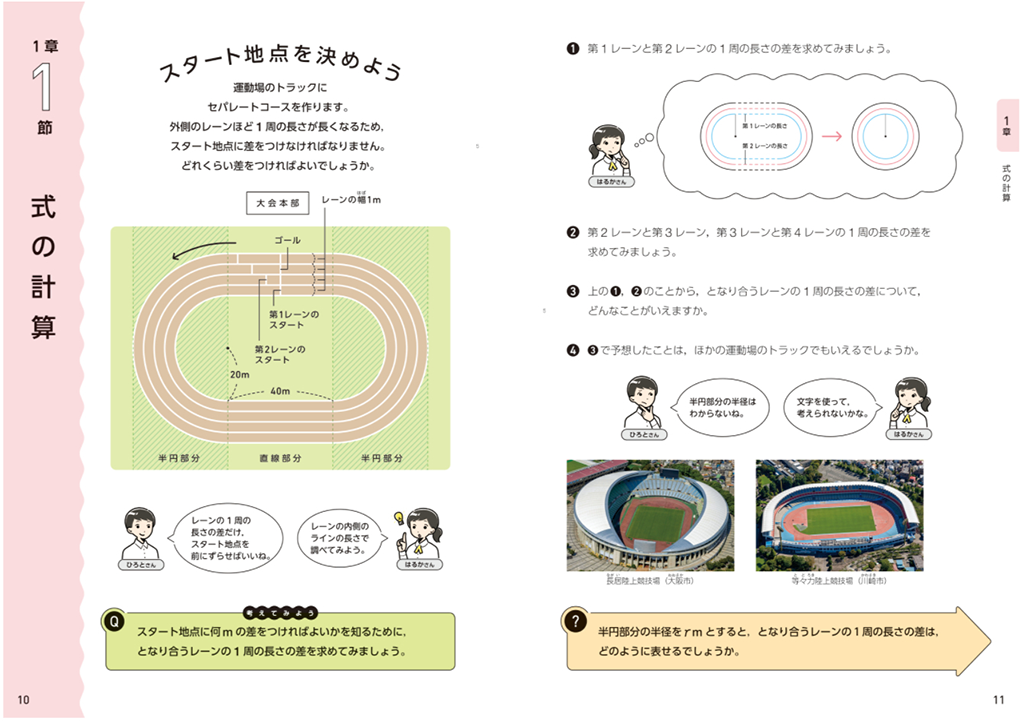
p.11の末尾の問いを受け、p.12のQでは、半径\(r\)mの円と半径 \((r+1)\)mの円の周の長さの差を求めます。

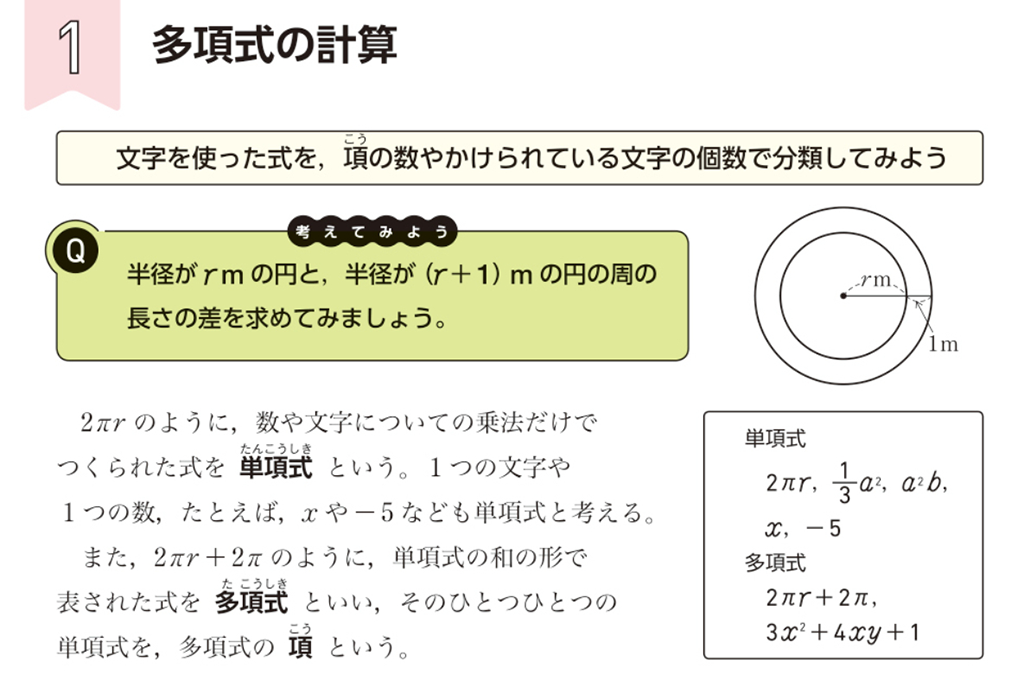
この計算結果「2\(\pi\)」の意味を、陸上トラックの問題場面に戻して解釈すると、以下のことがみえてきます。

① 第1レーンと第2レーンのスタート地点の差はいつでも2\(\pi\)mである

第1レーンの半円部分の半径を \(r\)mとすると、\(r\) がどんな値であっても、すなわち、半径がどんな大きさであっても、第1レーンと第2レーンのスタート地点の差はいつでも2\(\pi\)mであるということがわかります。

② 半円部分の半径は、となり合うレーンのスタート地点の差に関係しない

\(r\) を第2レーンや第3レーンの半円部分の半径と考えれば、すべてのとなり合うレーンにおいて、スタート地点の差が2\(\pi\)mになることがわかります。\(r\) の値がいくつであっても差が2\(\pi\)mで一定であるということは、半円部分の半径は、となり合うレーンのスタート地点の差に関係しないことを意味します。これは、\(r\) が計算の途中で消え、計算結果には含まれていないことからわかることです。

このような解釈は、生徒にとってはやや難しいですが、「一般的に表せる」「半径と差の関係がわかりやすくなる」といった、文字式のよさがわかる重要な見方です。

また、スタート地点の差を決めるしくみも明らかになるので、事象の理解も深まります。体育祭の準備にもぜひご活用ください。

関連記事はこちら

＞【2年1章】スタート地点を決めよう①