今日の授業のひと工夫（小中学校）

「新しい数学」2年1章では、陸上トラックのセパレートコースのスタート地点の差を調べます。

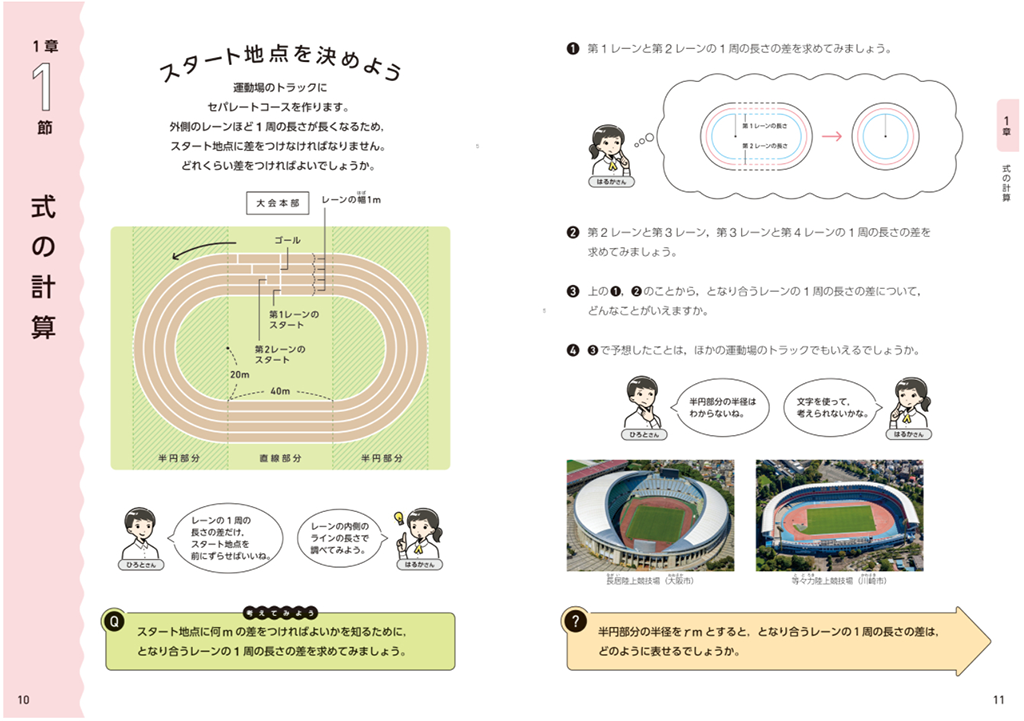
p.11の❶〜❸では、となり合うレーンの1周の長さの差について、具体的な数で考えます。

第1レーンと第2レーン、第2レーンと第3レーン、第3レーンと第4レーンの差をそれぞれ求めると、すべて2\(\pi\)mになることがわかります。このことから、となり合うレーンの1周の長さの差は、いつでも2\(\pi\)mで一定であると予想できます。

❹は、半円の半径と直線部分の長さを一般化し、どんな大きさの陸上トラックでもレーンの幅が1mであれば、スタート地点の差が2\(\pi\)mになることを説明する問いです。まず、ほかの運動場の写真を見せ、陸上トラックの大きさが様々であることを確認します。そして、❸で予想した「となり合うレーンの1周の長さの差は、いつでも2\(\pi\)mで一定であること」がほかの運動場の陸上トラックでもいえるのかという問題を設定していきます。

問題がつかめたら、実際に予想させるとよいでしょう。自分の考えをもつことで、解決する意欲につながります。そして、見通しを立てる段階では、半径や直線部分をどのように考えるかを問います。半円部分の半径がわからないことや、様々な形の陸上トラックがあることから、文字を使うことを思い出させ、p.11の？の問いにつなげたいところです。

p.12のQでは、半径rmの円と半径(r+1)mの円の周の長さの差を求めます。

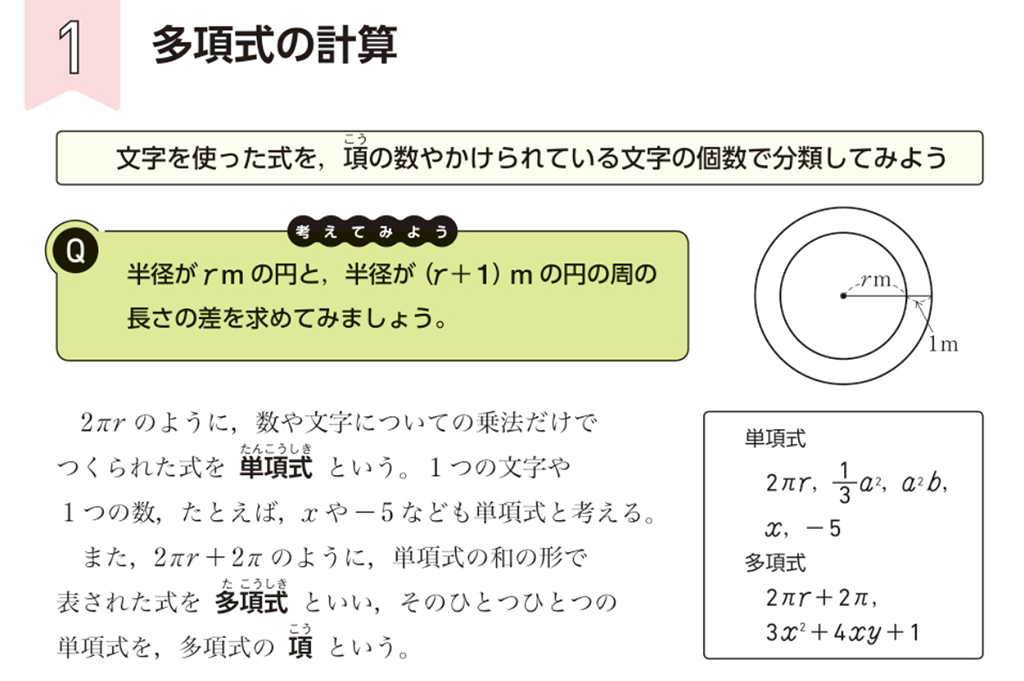
この差を求めるには、2\(\pi\)(r+1)-2\(\pi\)rを計算する必要があります。2\(\pi\)(r+1)の分配法則は未習ですが、生徒は違和感なく計算するでしょう。その際、「学習していないから計算できない」と決めつけるのではなく、生徒が直観的に行うことを認めたいところです。さらに「なぜそのように計算できるのかをこの単元で学習していこう」として、単元の見通しにつなげるようにしたいですね。

また、式 2\(\pi\)(r+1)-2\(\pi\)rを使って単項式と多項式の学習につなげることもこのQのねらいです。
Qを活用して、導入での日常場面の問題解決から、単項式と多項式の計算の学習へとつなげていきたいところです。

関連記事はこちら

＞【2年1章】スタート地点を決めよう②