今日の授業のひと工夫（小中学校）

2年7章では、コンビニエンスストアの店長の立場で、データに基づいて商品の売れ方を分析したり、仕入れる商品を意思決定したりする活動を行います。
　　　
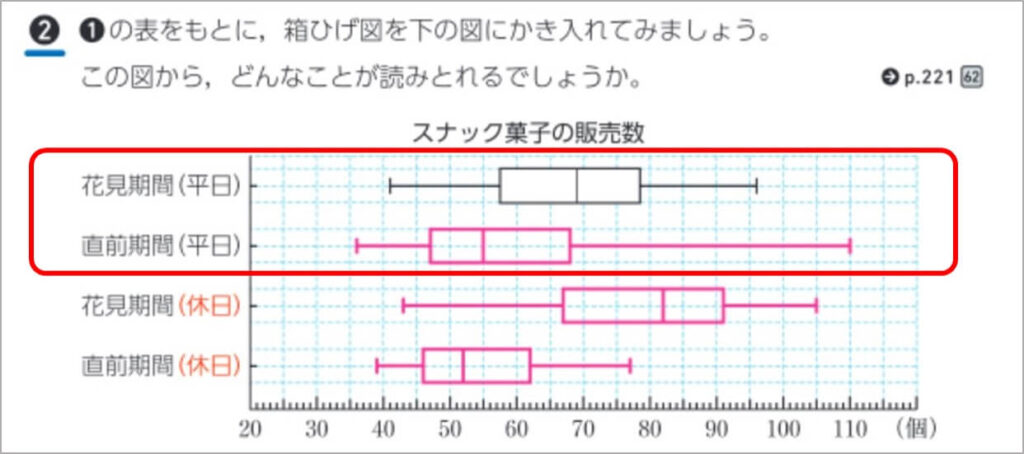
p.182では、スナック菓子の販売数のデータを箱ひげ図に表し、そこからどんなことが読みとれるかを考えます。
直前期間の平日の箱ひげ図のように、ひげの部分が極端に長い場合は、他と異質なデータ、すなわち外れ値が含まれている可能性があります。その可能性を考えずに、この区間にデータが散らばって存在していると捉えると、実際とは異なった分析結果になってしまいます。このような場合は、データに戻ったり、そのデータのヒストグラムを確認したりする必要があります。
外れ値の影響については、例えば「花見期間の平日で、もし120個売れた日が1日だけあったとしたら箱ひげ図はどうなるか」と問い、範囲は外れ値の影響を受けるけれど、四分位範囲はその影響を受けにくいことを実感させるとよいでしょう。

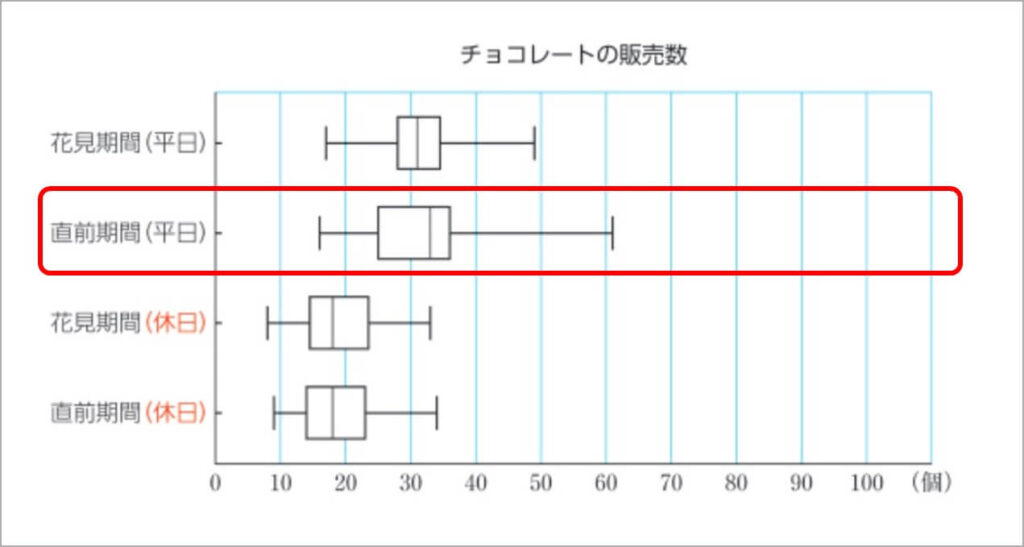
p.185のチョコレートの販売数についても同様に、直前期間（平日）の箱ひげ図では、第2四分位数と第3四分位数までの幅がとても狭く販売数が固まっているのに対し、右のひげがとても長いので、外れ値が含まれているかもしれない、という見方も培いたいところです。

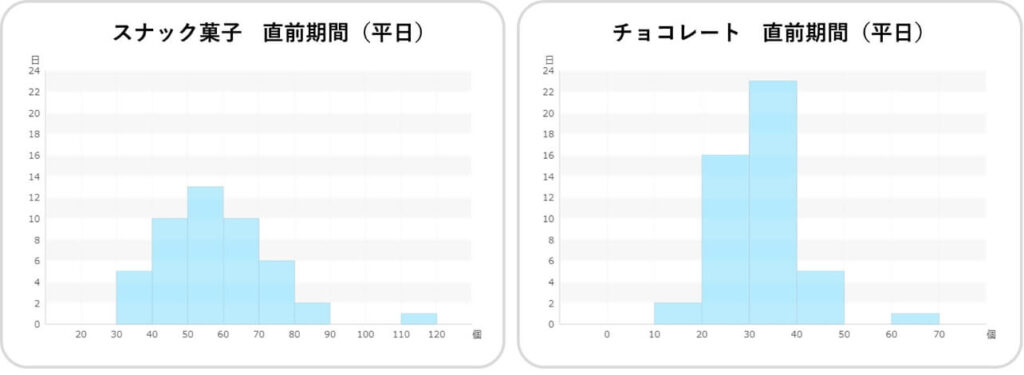
箱ひげ図は、複数のデータを比較するには便利ですが、細かい情報までは読みとれません。複数のデータを見比べて気になる特徴を見いだしたいときには、データに戻ったり、別のグラフを作成して考察したりする態度を培うことも大切です。今回の場合、ヒストグラムで確認すると、たしかに外れ値があることがわかります。

このように、箱ひげ図だけでなく、いろいろなグラフを用いていろいろな視点からデータを分析する姿勢を育んでいきたいですね。Dマークコンテンツを活用して、折れ線グラフや円グラフなど、さまざまなグラフで図示してみてはいかがでしょうか。