
長崎大学 教授
中川 幸久 先生
はじめに
高等学校の学習では,正弦や余弦は教科書や参考書にも頻出して馴染み深いが,正接についてはまとまった議論が少ない。
今回,「Tanθを楽しもう」と題して,高校の授業や発展学習等で取り組めるよう,以下の講義ごとにQA方式で整理してみた。
特に,直角を挟む2辺の長さが整数の直角三角形において,その一つの鋭角がいくつかの直角三角形の鋭角の和として表す方法を,複素数平面を活用して考察を深めた。複素数と整数論の融合とも言える。
研究を進める中で,その見分け方の一つとして連鎖探索法は極めて有効な一つの手段だと分かった。
しかしながら連鎖探索法はあくまでも見つけ方の手段であり,一般性を欠いており,まだまだ研究の余地を残している。授業では情報教育の一環としてプログラミングして求めていけば,さらにおもしろい発見があると思う。
最後には,二つの直角三角形の角の和や差の演算も導入して考察を深めてみた。
これまで扱われていない研究だから,先生方にとっても,生徒にとっても新鮮で興味深く感じるのではないだろうか。
なお,各講義には資料編として補足説明を加えるとともに,末尾に数学散歩と題して,正接に関わるものを整理している。これも併せてご一読いただきたい。
拙い研究であるが,多くの方々からのご意見を伺い,できるだけ高校生にもわりやすい教材を心掛けたい。
ぜひ,ご一読いただき,忌憚のないご感想をお寄せください。
| 講義1 | 「直角を挟む2辺の長さが整数の直角三角形の頂角で角を作る」 「横一列に並ぶ正方形のタイルの対角線で作る角の和が \(\frac{\pi}{4}\) となる場合」 |
| 講義2 | 「連鎖探索法による直角三角形の見つけ方」 |
| 講義3 | 「実際の算出法と連鎖探索法」 |
| 講義4 | 「加法と減法」 |
参考文献
“円周率.jp”(https://xn--w6q13e505b.jp/formula/arctan.html)※外部サイト
第1回 講義
講義のねらい
【直角を挟む2辺の長さが整数の直角三角形の頂角で角を作る】
我が家の風呂場の壁は,正方形のタイルが敷き詰められている。
適当に,対角線をとると鋭角ができるが,組み合わせるとどのような角が出来上がるのか,興味がわいた。
第一回講義のQ1にあるように,過去の教員採用試験の中で,正接が \(1,\frac{1}{2},\frac{1}{3}\) の角を加え合わせると,何故直角になるのかという問いがあった。
当然,正接が \(\frac{1}{2}\) と \(\frac{1}{3}\) の角で \(\frac{\pi}{4}\) になるのだが,他には組み合わせがないのか,2つ,3つ,4つの鋭角の和で表現することを試みた。
幾何学を,代数的な処理によって解決する。
そこに本講義の面白味がある。
1.直角を挟む2辺の長さが整数の直角三角形の頂角で角を作る
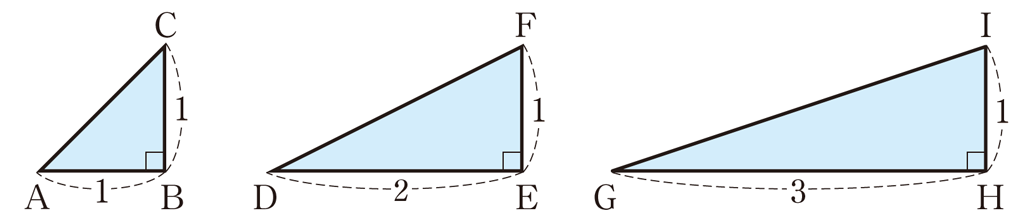
(過去の教員採用試験から)
下図において,\(\alpha + \beta + \gamma =\frac{\pi}{2}\) を示せ。
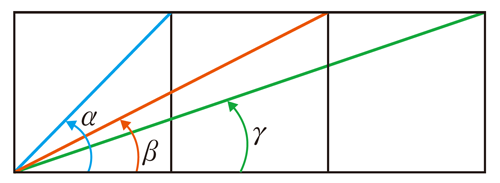
\(\tan \alpha =1,\tan \beta = \frac{1}{2},\tan \gamma = \frac{1}{3}\)
◎ \(\beta + \gamma = \frac{\pi}{4}\) を示せばよい。
明らかに \(\alpha = \frac{\pi}{4}\), \(\tan \beta = \frac{1}{2}\), \(\tan \gamma = \frac{1}{3}\)
\(\tan (\beta + \gamma)=\dfrac{\tan\beta + \tan \gamma}{1 – \tan\beta\tan\gamma}=\dfrac{\frac{1}{2} + \frac{1}{3}}{1 – \frac{1}{2}\cdot\frac{1}{3}} =1\)
\(0 \lt \beta + \gamma \lt \pi\) より \(\beta + \gamma = \frac{\pi}{4}\)
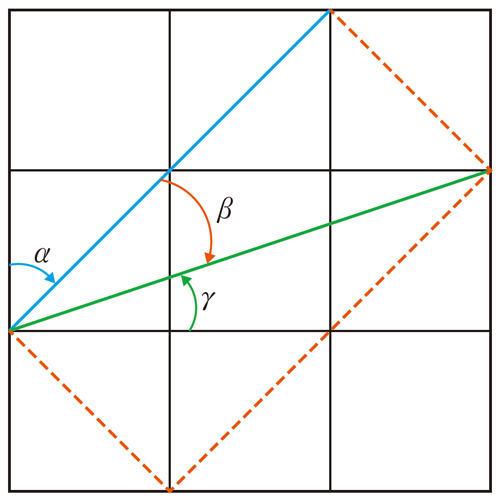
3点 \(\text{A}\),\(\text{D}\),\(\text{G}\) をそれぞれ原点に,3点 \(\text{C}\),\(\text{F}\),\(\text{I}\) を複素数平面上の \(\text{C}(1+i)\),\(\text{F}(2+i)\),\(\text{I}(3+i)\) に対応させる。
\(\alpha + \beta + \gamma = arg(1+i)+arg(2+i)+arg(3+i)\)
\(\hspace{88px}=arg(1+i)(2+i)(3+i)\)
\(\hspace{88px}=arg \{(6-1-2-3)+(2+6+3-1)i \}\)
\(\hspace{88px}=arg(10i)=\frac{\pi}{2}\)
正接の加法定理 \(\tan(\alpha + \beta)=\dfrac{\tan\alpha + \tan \beta}{1-\tan \alpha\tan\beta}\) から
\(\tan(\alpha+\beta+\tau)=\dfrac{\tan(\alpha+\beta)+\tan\tau}{1-\tan(\alpha+\beta)\tan\tau}\)
\(\hspace{130px}=\dfrac{\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}+ \tan\tau}{1-\frac{\tan\alpha + \tan\beta}{1-\tan\alpha\tan\beta}\cdot\tan\tau}\)
\(\hspace{130px}=\dfrac{\tan\alpha + \tan\beta + \tan\tau – \tan\alpha\tan\beta\tan\tau}{1-\tan\alpha\tan\beta – \tan\beta\tan\tau – \tan\tau\tan\alpha}\)
直角を挟む2辺が整数である直角三角形の正接は有理数なので2つの角の和や3つの角の和の正接も有理数となる。
帰納的に,直角を挟む2辺が整数であるいくつかの直角三角形の頂角の和の正接は有理数になる。
一方,\(\frac{\pi}{6},\frac{\pi}{3}\) の正接は \(\tan \frac{\pi}{6}=\frac{1}{\sqrt{3}},\tan \frac{\pi}{3}=\sqrt{3}\) の無理数である。
したがって,直角を挟む2辺が整数であるいくつかの直角三角形の頂角を合わせても \(\frac{\pi}{6},\frac{\pi}{3}\) にならない。(資料1-①)
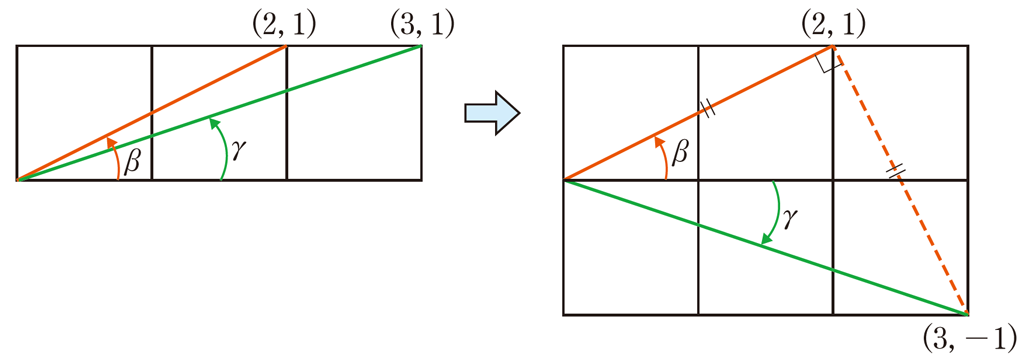
2.横一列に並ぶ正方形のタイルの対角線で作る角の和が \(\frac{\pi}{4}\) となる場合
下図のように,正方形のタイルが横に一列に並んでいる。
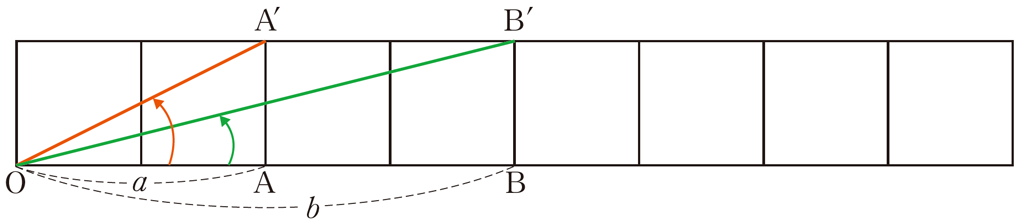
\(\theta = \frac{\pi}{4}\) となる2点 \(\text{A,B}\) の位置を求めよ。
ここで複素数平面に対応して考えてみる。
\(z_{1}=a+i,z_{2}=b+i\) とする。
\(\angle \text{AOA}’=arg(z_{1}),\angle \text{BOB}’=arg(z_{2})\) だから
\(\theta=arg(z_{1})+arg(z_{2})=arg(z_{1}z_{2})\)
\(z_{1}z_{2}=(a+i)(b+i)=(ab-1)+(a+b)i\)
実部 \(=ab-1\),虚部 \(=a+b\) である。
\(\theta=\frac{\pi}{4}\) は実部と虚部が等しいので
\(ab-1=a+b\)
\(ab-a-b=1\)
\((a-1)(b-1)=2\)
\(0 \leqq (a-1) \leqq (b-1)\) より
\((a-1,b-1)=(1,2)\)
これを満たす(\(a,b)\) は \((a,b)=(2,3)\)
以上より,\(\theta =\frac{\pi}{4}\) は,\((a,b)=(2,3)\) 以外にはない。
下図のように,正方形のタイルが横に一列に並んでいる。
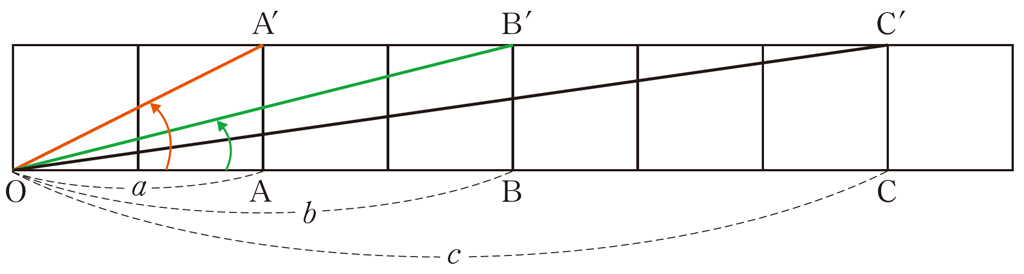
\(\theta = \frac{\pi}{4}\) となる3点 \(\text{A,B,C}\) の位置を求めよ。
ここで複素数平面に対応して考えてみる。
\(z_{1}=a+i,z_{2}=b+i,z_{3}=c+i\) とする。
\(z_{1}z_{2}z_{3}=(a+i)(b+i)(c+i)\)
\(\hspace{59px}=(abc-a-b-c)+(ab+bc+ca-1)i\)
\(\theta =\frac{\pi}{4}\) は,実部と虚部が等しいので
\(abc-a-b-c=ab+bc+ca-1\)
\(abc+1=(a+b+c)+(ab+bc+ca)\) …①
\(1\leqq a \leqq b \leqq c\) より
\(abc+1=(a+b+c)+(ab+bc+ca)\leqq 3c+3bc\)
ここで \(a,b,c\) を絞り込む。
\(abc \lt abc + 1 \leqq 3c+3bc\)
\(ab \lt 3+3b\)
\((a-3)b \lt 3\) …②
\(a \geqq 4,b \geqq 4\) とすると②は成り立たないので \(a \leqq 3\) である。
\(a=1\) のときは,明らかに \(\theta \gt \frac{\pi}{4}\) となるので,\(a=2\) または \(a=3\) である。
(1) \(a=2\) のとき
①より
\(2bc+1=2+b+c+ab+bc+2c\)
\(bc-3c-3b-1=0\)
\((b-3)(c-3)=10\)
\(b-3 \leqq c-3\) より
\((b-3,c-3)=(1,10),(2,5)\)
\((a,b,c)=(2,4,13),(2,5,8)\)
(2) \(a=3\) のとき
①より
\(3bc+1=3+b+c+3b+bc+3c\)
\(bc-2b-2c-1=0\)
\((b-2)(c-2)=5\)
\(b-2\leqq c-2\) より
\((b-2,c-2)=(1,5)\)
\((a,b,c)=(3,3,7)\)
以上より,\(\theta =\frac{\pi}{4}\) は,\((a,b,c)=(2,4,13),(2,5,8),(3,3,7)\) 以外にはない。
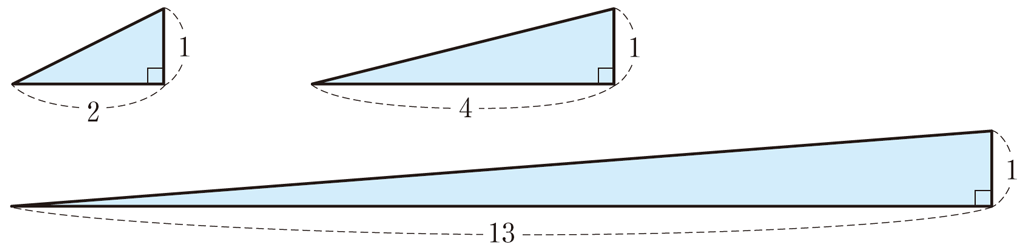
【まとめ】高さ1の3つの直角三角形の鋭角の和 \(\theta = \frac{\pi}{4}\) は,以下の3通り。
(ア)\((2,4,3)\) … \((2,1)\) と \((4,1)\) と \((13,1)\) の三角形
(イ)\((2,5,8)\) … \((2,1)\) と \((5,1)\) と \((8,1)\) の三角形
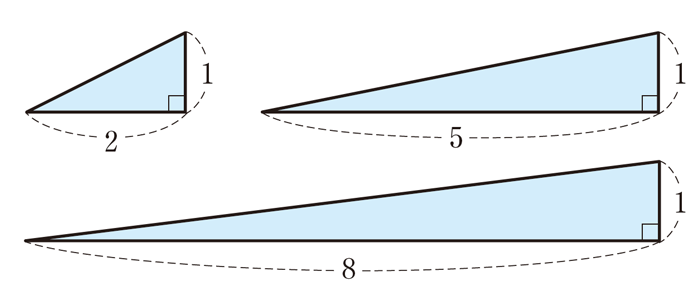
(ウ)\((3,3,7)\) … \((3,1)\) と \((3,1)\) と \((7,1)\) の三角形
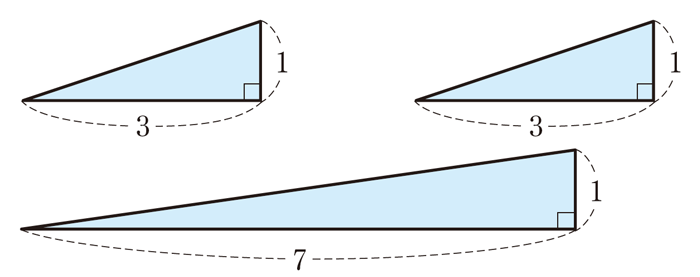
以上を,\(\theta =\frac{\pi}{4}\) となる三角形を \((1,1)\) とし,以下のように書き表す。
2つの三角形の角の和
\((1,1)=(2,1)+(3,1)\)(算出1)
3つの三角形の角の和
\((1,1)=(2,1)+(4,1)+(13,1)\)(算出2)
\((1,1)=(2,1)+(5,1)+(8,1)\)(算出3)
\((1,1)=(3,1)+(3,1)+(7,1)\)(算出4)
下図のように,正方形のタイルが横に一列に並んでいる。
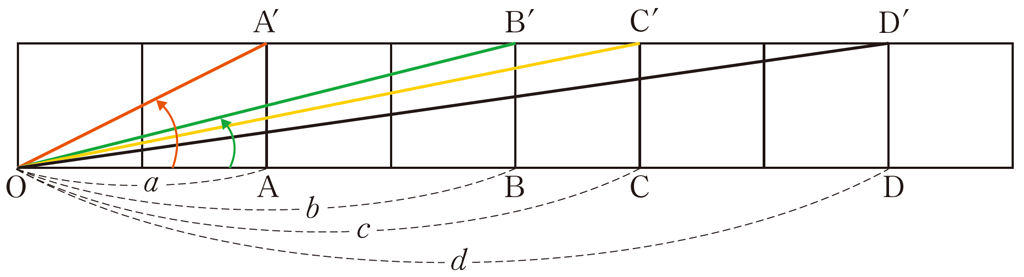
ここで複素数平面に対応して考えてみる。
\(z_{1}=a+i,z_{2}=b+i,z_{3}=c+i,z_{4}=d+i\) とする。
\(\angle \text{AOA’}=arg(z_{1}),\angle \text{BOB’}=arg(z_{2}),\angle \text{COC’}=arg(z_{3}),\angle \text{DOD’}=arg(z_{4})\) より
\(\theta=arg(z_{1})+arg(z_{2})+arg(z_{3})+arg(z_{4})=arg(z_{1}z_{2}z_{3}z_{4})\)
\(z_{1}z_{2}z_{3}z_{4}=(a+i)(b+i)(c+i)(d+i)\)
\(=(abcd-ab-ac-ad-bc-bd-cd+1)+(abc+abd+acd+bcd-a-b-c-d)i\)
(実部) \(=abcd-ab-ac-ad-bc-bd-cd+1\)
(虚部) \(=abc+abd+acd+bcd-a-b-c-d\)
\(\theta =\frac{\pi}{4}\) は,\(z_{1}z_{2}z_{3}z_{4}\) の実部と虚部が等しいときである。
\(abcd-ab-ac-ad-bc-bd-cd+1=abc+abd+acd+bcd-a-b-c-d\)
解法は,資料に追記するが,求める \((a,b,c,d)\) は,以下の15通りである。
\((a,b,c,d)=(2,4,14,183),(2,4,15,98),(2,4,18,47),(2,4,23,30)\)
\((a,b,c,d)=(2,5,9,73),(2,5,13,21)\)
\((a,b,c,d)=(2,6,7,68),(2,6,8,31)\)
\((a,b,c,d)=(2,7,8,18)\)
\((a,b,c,d)=(3,3,8,57),(3,3,9,32),(3,3,12,17)\)
\((a,b,c,d)=(3,4,5,47),(3,4,7,13)\)
\((a,b,c,d)=(3,5,7,8)\)
4つの三角形の角の和で表すと以下の15通り。解説は(資料1-②)で紹介。
4つまでの三角形の角の和は全部で19通り。
\((1,1)=(2,1)+(4,1)+(14,1)+(183,1)\)(算出5)
\((1,1)=(2,1)+(4,1)+(15,1)+(98,1)\)(算出6)
\((1,1)=(2,1)+(4,1)+(18,1)+(47,1)\)(算出7)
\((1,1)=(2,1)+(4,1)+(23,1)+(30,1)\)(算出8)
\((1,1)=(2,1)+(5,1)+(9,1)+(73,1)\)(算出9)
\((1,1)=(2,1)+(5,1)+(13,1)+(21,1)\)(算出10)
\((1,1)=(2,1)+(6,1)+(7,1)+(68,1)\)(算出11)
\((1,1)=(2,1)+(6,1)+(8,1)+(31,1)\)(算出12)
\((1,1)=(2,1)+(7,1)+(8,1)+(18,1)\)(算出13)
\((1,1)=(3,1)+(3,1)+(8,1)+(57,1)\)(算出14)
\((1,1)=(3,1)+(3,1)+(9,1)+(32,1)\)(算出15)
\((1,1)=(3,1)+(3,1)+(12,1)+(17,1)\)(算出16)
\((1,1)=(3,1)+(4,1)+(5,1)+(47,1)\)(算出17)
\((1,1)=(3,1)+(4,1)+(7,1)+(13,1)\)(算出18)
\((1,1)=(3,1)+(5,1)+(7,1)+(8,1)\)(算出19)
(第2回につづく)
【講師】
長崎大学 教育開発推進機構
アドミッションセンター教授
中川 幸久 先生

長崎大学教育学部数学科卒業後,長崎県内の高等学校で教諭,教頭,校長を歴任。長崎県教育委員会で人事管理監,高校課長,教育次長を経て退職。長崎県立図書館長を経て,2015 年より現職。地域貢献として,長崎県 NIE 推進協議会会長,長崎県明るい選挙推進協議会会長を歴任する。現在,長崎県数学教育会会長,九州数学教育会理事を務める。
その他のコンテンツ
