
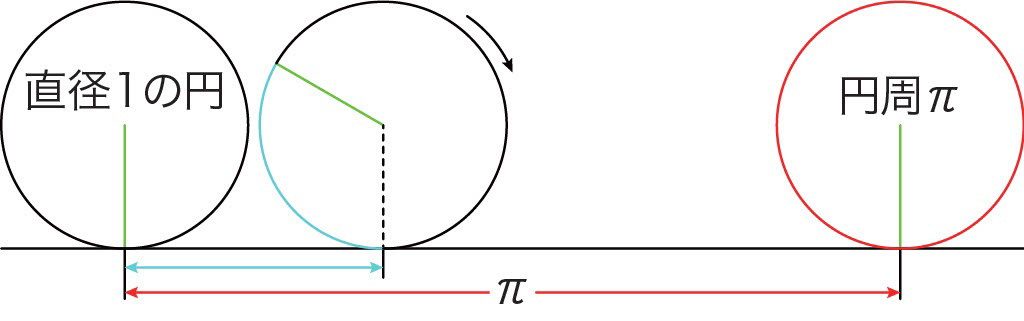
今日は,タイヤを地面の上で滑らないように1回転転がします。

地面の青い線分の長さがタイヤの直径の \(\pi\) 倍になっているはずです。それはタイヤの周長と同じ長さです。つまり,1回転転がした後の右側のタイヤの青色の周長と同じ長さです。
本題はここからです。
タイヤとともにホイールもちょうど1回転しています。
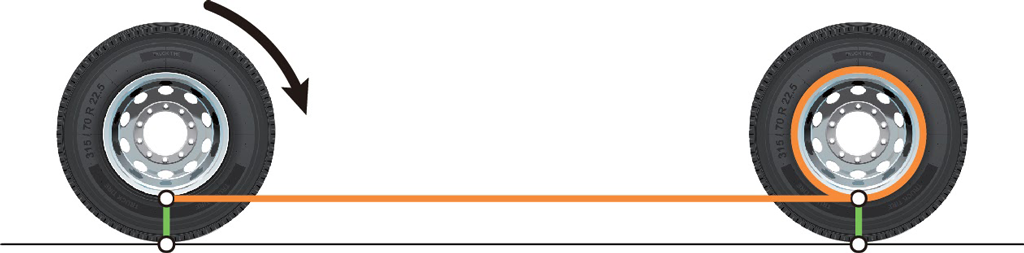
ホイールの移動距離はオレンジ色の線分の長さです。ホイールはちょうど1回転しているのだから,その長さは,オレンジ色に塗ったホイールの周長に等しいはずです。
一方,タイヤとホイールの移動距離は等しいです。つまり,青い線分の長さとオレンジ色の線分の長さは同じです。
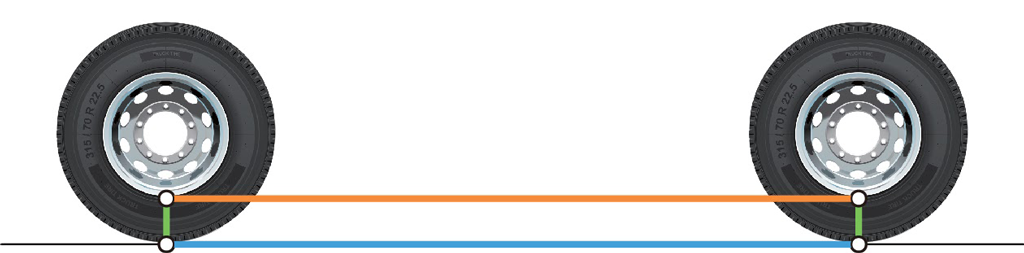
ということは,青色の円周の長さとオレンジ色の円周の長さが等しいことになります。
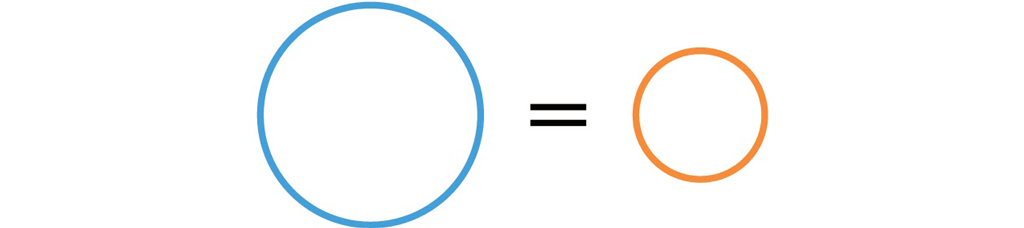
【疑問】明らかにヘンですね。どこが(何が)ヘンなのでしょうか。
これを認めたらどんな円の円周も等しい長さをもつことになります。だからヘン,ということもできます。この「ヘン」の説明は,結論がおかしいから,いままでの議論のどこかが間違っているということを指摘しています。が,どこがヘンなのかは指摘していません。
最初のタイヤを転がした図から上の「等式」まで,論理的に話を展開してきました。だから,結論がヘンということは,推論のどこかに「ヘン」が紛れ込んでいるとしか考えられません。それはどこでしょうか。(※ 推論=論を推し進めること。)
この疑問に答えるために,タイヤを少し転がしたときの図を描いてみます。見やすくするためにタイヤは描かないことにしましょう。
次の図は,左端の円を,130度と360度,それぞれ滑らないように転がしたときの図です。
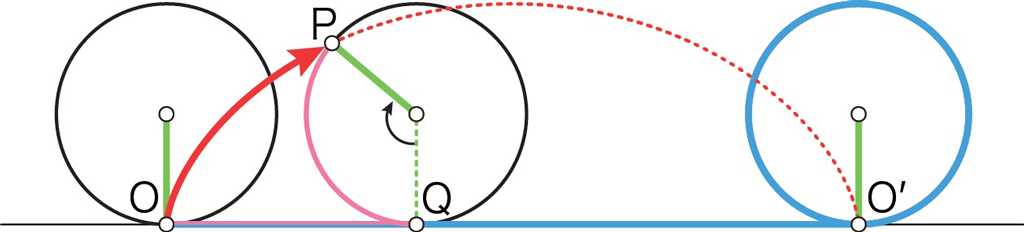
点Pは点Oから転がり始めて,130度転がったとき,赤い矢印の曲線の軌跡を辿ります。(点Pはその後360度回転するまで赤色の破線の軌跡を辿ります。いわゆるサイクロイドです。)
このとき,円の移動距離はピンク色の線分OQの長さです。
一方,ピンク色の円弧PQは130度回転する間に地面に滑らずに転がりながら接触した部分です。だから,線分OQの長さと円弧PQの長さは同じです。
次に,同じことをホイールについて考えます。
次の図で,ピンクの線分の長さは130度回転したときにホイールの移動距離に他なりません。これはタイヤの移動距離に等しいです。(赤色の曲線はホイールの枠上の点の軌跡です。サイクロイドではありません。トロコイドと呼ばれます。)
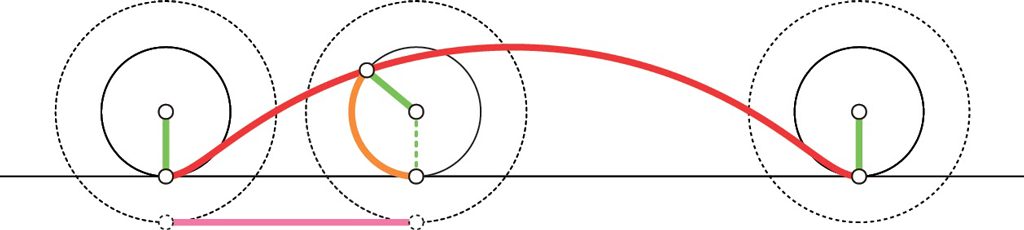
ところが,オレンジ色のホイールの円弧は,ホイールの高さに水平線(黒色の実線)を引いたときの,「130度回転する間にその水平線に転がりながら接触した部分」です。
しかし,動く歩道の上でホイールを回しているようなもので,移動しながら回転しています。
つまり,水平線の上をホイールを転がしたとみなした場合,ホイールは少しずつ滑りながら回転しているのです。もし滑っていなかったら,ピンクの線分の長さほど移動しないはずだからです。
こういうことは,むしろ式で表した方がわかりやすいかもしれません。

これは滑るということを定量的に表現した式といえます。
これでもちょっと不満かもしれません。
そこで,もっと比較がはっきりするように,ホイールの内側の円に対して同じ操作を考えます。(赤色の曲線はホイールの内側の円上の点の軌跡です。サイクロイドからますます遠ざかった曲線です。これもトロコイドです。)
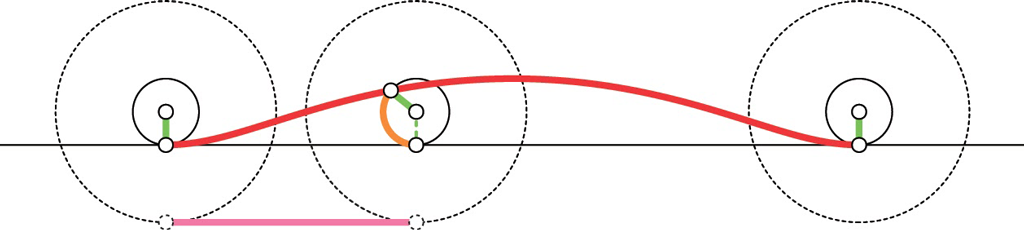
これくらい小さい円を考えると,明らかに移動した長さと円弧の長さの違いがはっきりしますね。
究極を考えましょう。タイヤやホイールの中心の動きはどうなるでしょうか。
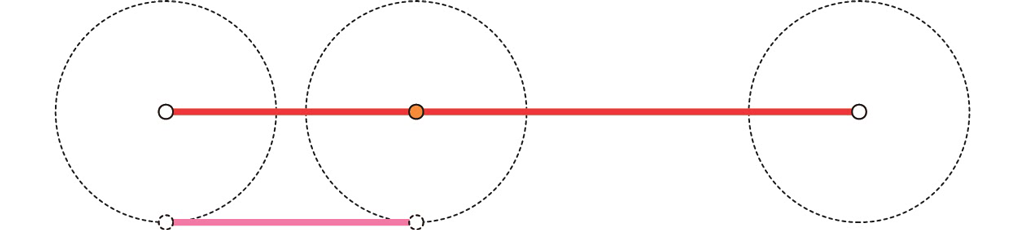
そうです。水平に移動するだけです。半径0の円の円弧の長さは0ですから,上の等式から,
(移動した長さ)=(滑った長さ)
であることがわかります。つまり中心は水平に滑っているだけです。
滑る滑らないを物理的に考えると,摩擦のことを考えなくてはならなくなるでしょう。
一方,数学的には,ホイールが移動した長さと円弧の長さにギャップがある場合,そのギャップをもたらす原因を滑りと呼ぶ,と定義することができます。
※この定義は分子レベルで考えたものではなく,直線や曲線といった数学的概念を用いたものであるので,数学的な滑りを定義したといった方が正確です。
アリストテレスの贈り物
アリストテレスは紀元前350年ころに活躍した古代ギリシアの哲学者です。アルキメデスの100年前くらいの人です。
今回の話は,『アリストテレスの車輪』と呼ばれるパラドックスです。アリストテレスが『小品集Opuscula』の「機械学 第24章」において,「より大きい円がより小さい円と同じ中心にそって置かれるとき(同心円),小さい円と等しい長さの線を転回するのは一体何故であるかということが問題である」と問いかけて,自答しました。その答えは,座標やベクトル,速度などを使っていない上に,「滑る」ことに関して直観的な記述もあるため,スッキリとした回答には見えません。それに不満をもったガリレオ・ガリレイは『新科学対話』の第1日目で同問題を扱い,タイヤとホイールに見立てた大小の正 \(n\) 角形を転がして,「滑る」ことの理解を深めました。確かに正 \(n\) 角形を転がすと,ホイールに対応する小さい正 \(n\) 角形が「滑る」ことがよくわかります。ガリレオはアリストテレスの車輪を近似的に解決したといえるでしょう。
しかし,アリストテレスの車輪のもやもやが解消されたとは思えません。同心円の中心から動径を引くと,タイヤとホイールの円周に1回ずつ交わります。つまり,タイヤとホイールの円周の各点は1対1対応しています。もやもやの原因は,二つの無限集合の各要素が1対1対応になっていることと,それぞれの無限集合の大きさ(長さ)が等しいか否かは別の話であるということです。例えば,正接関数 \(\text{tan}\theta\) は,長さ \(\pi\) の有限区間 \(\left(- \frac{\pi}{2},\frac{\pi}{2} \right)\) と長さ無限の無限区間 \((-\infty,\infty)\) の各点を1対1対応させますが,各区間の長さは全く異なります。数学的には集合の濃度と長さの話です。これらはそれぞれ1900年前後にカントールとルベーグによって整備されました。1600年くらいのガリレオから300年後の話です。
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
