特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

令和6年度全国学力・学習状況調査の結果を生かした授業づくり②

Q　前回の記事の全国学力・学習状況調査の結果を分析した「回転移動」の指導例を見て、調査の結果を根拠にした授業づくりを大切にしたいと思いました。他の指導例も教えてください。

Ａ　今回は、領域C「関数」について前号と同じように、全国学力・学習状況調査の結果を踏まえた指導の改善・充実の例について一緒に考えましょう。

　前回は令和6年度全国学力・学習状況調査結果を生かした指導の改善・充実について考えました。調査を受けた3年生の生徒に対して結果に応じた個別の指導が行われること、また、調査結果から明らかになったつまずきを解答類型で把握し、それを生かした授業づくりが大切であることをお伝えしました。今回は、領域C「関数」での問題で考えてみましょう。

□中学校数学　大問4「一次関数」について

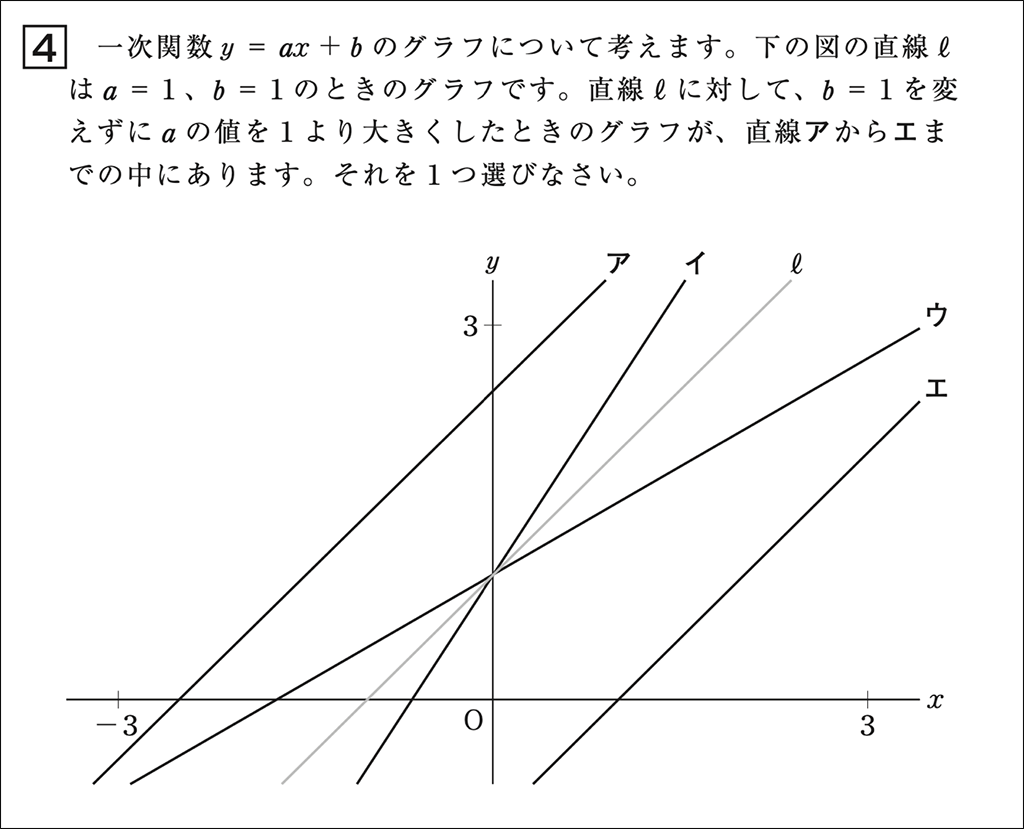
令和6年度全国学力・学習状況調査問題大問4

　本問は、第2学年の関数領域、一次関数の特徴についての理解を評価する問題です。一次関数の特徴は表、式、グラフを関連付けて理解することは大切であり、教科書でも下のように取り上げられています。一方でその確実な理解のために、授業では生徒へ一方的に伝えてしまうことがないでしょうか。

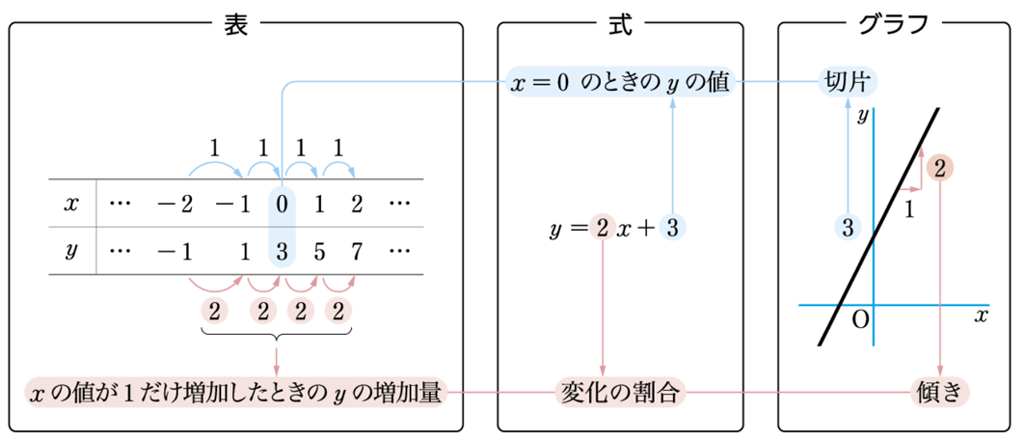
教科書での一次関数の表、式、グラフの関連の記載（新しい数学2 p.70）

　この問題について報告書をみてみると、正答である「イ」を選択した反応率は65.6％で課題があると報告されています。誤答である「ア」を選択した生徒は8.5％、「ウ」を選択した生徒は17.7％、「エ」を選択した生徒は7.5％でした。これらから、本問において一次関数 \(y=ax+b\) の \(a\) の値を1より大きくした場合にグラフの傾きぐあいに着目した解答は「イ」と「ウ」で、その反応率は83.8％です。ほとんどの生徒が一次関数 \(y=ax+b\) の \(a\) の値を1より大きくしたとしても、グラフの切片（\(y\) 軸との交点）の位置に影響しない理解していると解釈できます。このように捉えていない生徒の反応率は「ア」と「エ」の16.0％ですが、無視できるものではありませんので個別に指導は必要です。このことを踏まえて、授業づくりを考えてみましょう。

□本問及び調査結果を生かした授業づくり

　一次関数の特徴について理解するために、その特徴を明らかにすることを生徒一人一人の自分事の問いとなるように工夫し、考察する活動を展開することが大切です。例えば、前時までに一次関数 \(y=ax+b\) の「\(b\) の値」とグラフでの「\(y\) 軸との交点の位置」についての関係を考察し、一次関数の切片の特徴を見いだした生徒が、“それなら”として問い、「一次関数 \(y=ax+b\) の \(a\) の値を大きくしたり、小さくしたりするとどのようなグラフになるのか」について考察する場面を設定するとよいです。 ここで、前回の「回転移動」のときと同じようにDマークコンテンツを1人1台端末で利用することで、一次関数 \(y=ax+b\) の \(a\) の値の大きさによるグラフの特徴について考察する活動を充実させることができます。

①　一次関数 \(y=ax-1\) について、\(a\) の値をだんだん大きくしたときのグラフを観察する

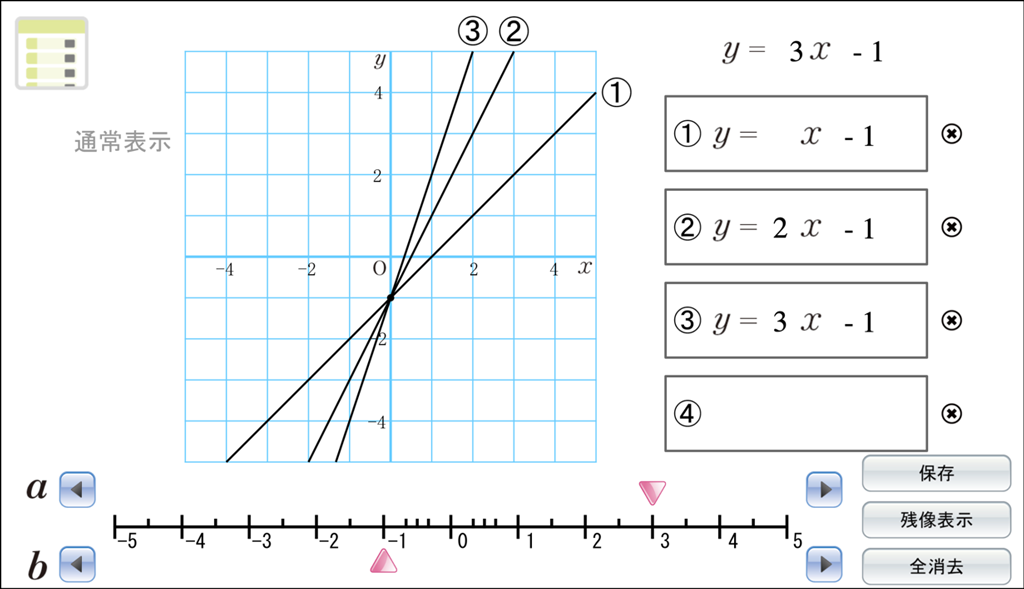
「新しい数学2」Dマークコンテンツ「1次関数のグラフを調べよう」

②　一次関数 \(y=ax-1\) について、\(a\) の値を大きくしたときのグラフの残像を残して考える

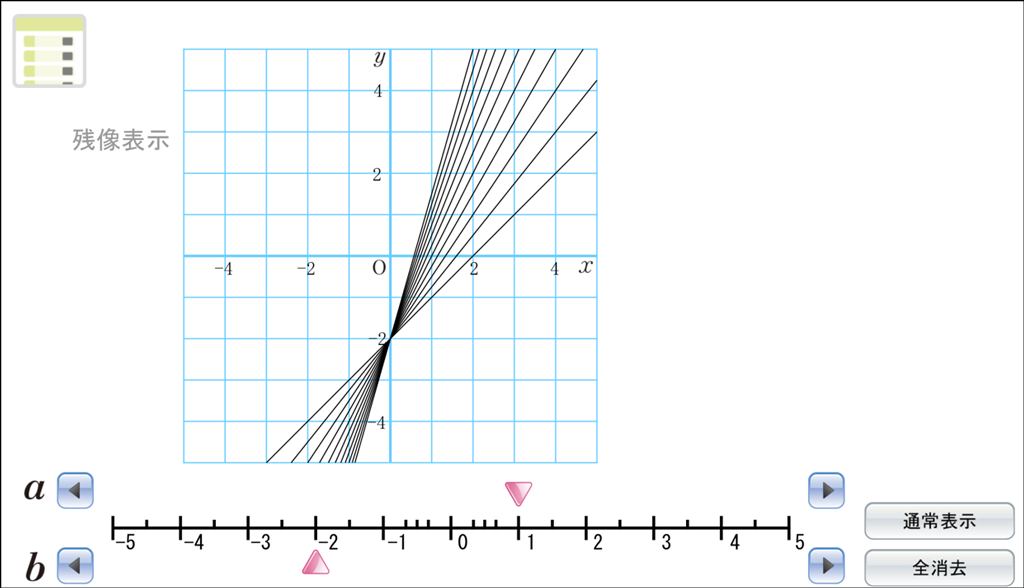
「新しい数学2」Dマークコンテンツ「1次関数のグラフを調べよう」

　このDマークコンテンツを使用することで、観察や操作、実験を通した授業を展開することができます。生徒は、一次関数 \(y=ax+b\) の \(a\) の値をだんだんと大きくすることで、グラフの傾き具合が急になると捉えるでしょう。この活動において留意すべきことは、コンテンツでの観察のみで結論の表出とするのではなく、これまでに学習した「変化の割合」を併せて考える場面を設定することです。そうすることによって、一次関数 \(y=ax+b\) の \(a\) の値とそれ応じたグラフの特徴について、実感を伴って理解することができるようになります。
　さらに、下のようなDマークコンテンツを使用することも考えられます。このコンテンツでは、一次関数 \(y=ax+b\) の \(a\) や \(b\) の値を自分で変えることができ、表、式、グラフを関連させながら、一次関数の特徴を確認することができます。

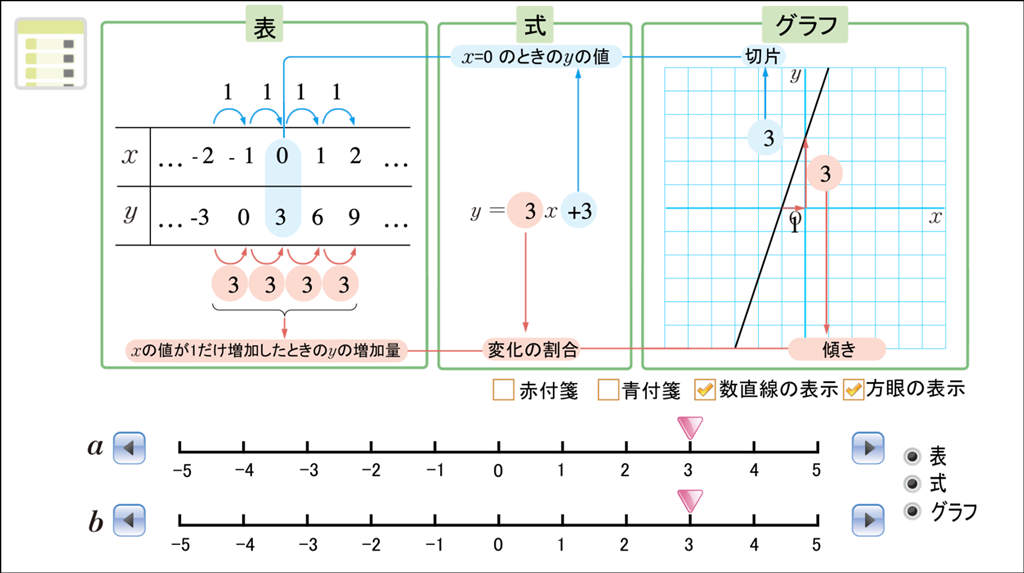
「新しい数学2」Dマークコンテンツ「表・式・グラフの関連を調べよう」

　一次関数の特徴を理解するためには、授業で一次関数 \(y=ax+b\) の \(a\) や \(b\) の値やその大きさに着目して、式とグラフの関連付けて考察することが大切です。全国調査の結果について参考にしながら、「知っている」にとどまらず、「わかる」といった概念的な理解につながるような授業づくりに取り組み、実践してみましょう。

Dマークコンテンツ「1次関数のグラフを調べよう」はこちら

Dマークコンテンツ「表・式・グラフの関連を調べよう」はこちら

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。

※参考資料

• 令和6年度全国学力・学習状況調査報告書中学校数学（国立教育政策研究所）
• 「新しい数学2」（東京書籍）
• 「新しい数学2」Dマークコンテンツ https://tsho.jp/03j/m2/

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。