
はじめに
起床から就寝まで,もしかしたら夢の中でも,まったく一瞬たりとも何も考えることがない日はないでしょう。「考える」を次のように程度によって2種類にわけてみます。
一つは,どうしたら試合に勝てるだろうか,どうしたら仕事を上手に回せるだろうか,良い成績を収めるにはどうしたらよいだろうか,目の前の問題を熟考する,などという本格的に自覚して「よく考える」ことです。
もう一つは,もっと素朴に,今日は暑い,なんで? 今日は赤信号によくひっかかる,どうして? 今日は人通りが多い,何かあるの? などと,一瞬考えて,すぐに理由が何となくわかって,あるいは(深く)考えるほどのことではないと判断して,考えるのをやめる程度の「つい考える」ことです。つい考えることは,しょっちゅうあることだと思います。
その程度のつい考えることでも,納得する回答が得られたら,すっきりしますし,何かをクリアーして得した気分になることもしばしばでしょう。
本連載の趣旨は,そのようについ考えることをきっかけとして,もうちょっとだけついつい考えたり,新しい疑問が湧いたり,もっと考えて没頭したり,・・・といった感じに,つい考えることからの展開を楽しむことです。
言い換えると「つい考えてしまう考えること」の紹介です。そして,その考えることに数学が含まれていること,いやむしろ,読者の皆さんが,考えること自体を数学というのだ,と実感できるような連載になりましたら幸いです。
2024年8月吉日 矢崎成俊
軸上に長さ\(\pi\)の目盛りを描く

1円玉の直径は2cmなので,周長は 2\(\pi\) cmです。だから6cm以上なのですが,1円玉を手にとると,円周が6cm以上あるとはどうも思えません。目の錯覚でしょうか。
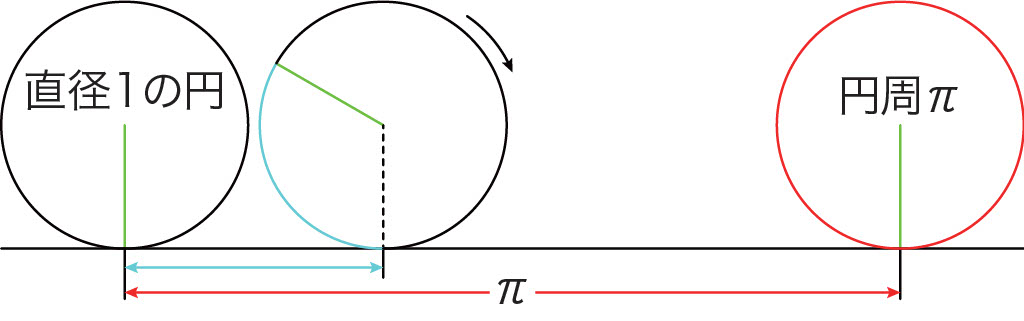
円周は直径の \(\pi\) 倍です。だから,直径 \(1\) の円をすべらないように直線上を転がして,円がちょうど1周したとき,転がった距離は \(\pi\) になります。この図を見ると,ますます円周よりも長さ \(\pi\) の線分の方が長く見えませんか。
長く見えるとしたらそれは目の錯覚ですから,やはり円周を直接測って納得するのがよいでしょう。測る方法はいくつか考えられます。
- 円柱状の容器などの円周をひもでちょうど1周分移しとって,ひもを伸ばしてもの差しで測る。
- あるいは,円周を直接巻き尺で測る。
- チーズを入れているような円盤状の丸い紙の容器や,トイレットペーパーの芯などを鋏で切って,真っ直ぐに伸ばして,もの差しで測る。
皆でわいわいとチャレンジしてみてください。いずれの方法でも直径の3.14倍のように小数点以下2桁まで精度良く計測できたら大変素晴らしいです。

【疑問】実際の計測では誤差がつねに入り込みます。そこで,理論上でよいので,この図のように直線の上に長さ\(\pi\)の線分を書くことはできるでしょうか。
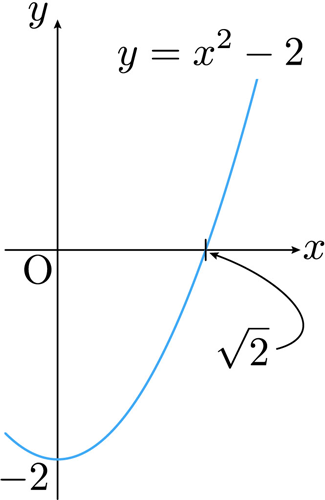
例えば,\(\sqrt{2}\) は,放物線 \(y=x^2-2\) の \(x\) 切片(の正の方)として与えられます。これは面積 \(2\) の正方形の一辺の長さを求めることに等しい操作(考え方)といえます。
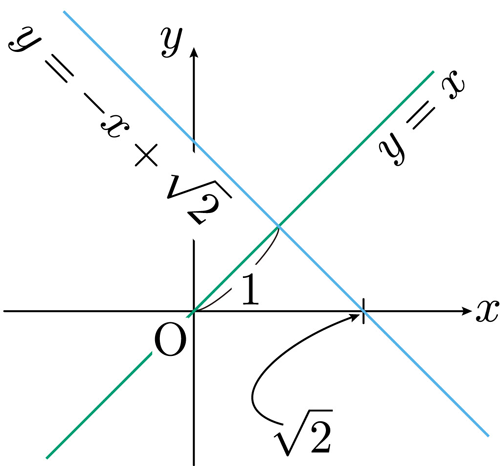
もちろん,\(\sqrt{2}\) は,1辺の長さ \(1\) の単位正方形の対角線の長さとして与えられるので,\(y=x\) 上で,原点から \(1\) の距離にある第1象限の点で \(y=x\) に直交する傾き \(-1\) の直線の \(x\) 切片が \(\sqrt{2}\) となります。
ただし,直線の方程式が \(y=-x+\sqrt{2}\) となり,\(\sqrt{2}\) の切片を求めたいのに,方程式ですでに \(\sqrt{2}\) を使うことになって,少々不満が残ります。
不満はともかく,いずれの場合も,曲線や直線の \(x\) 切片として,\(\sqrt{2}\) が求まります。
【疑問の深堀り】\(\pi\) は曲がった円周の長さです。言い換えると,回転角ともいえます。上であげた疑問を深堀りすると,角度を直線上の線分の長さとして表現できるか,という疑問になるでしょう。
アルキメデスは,ある曲線を使って,この疑問を見事に解決しました。
(後編に続く)
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
