
(前編はこちら)
アルキメデスによる線分 \(\pi\) の作成方法を紹介しましょう。
まず,時計は針が右回りに回りますが,軸とのなす角度は,左回り,つまり反時計回りに大きくなっていきます。いま時計の針のように原点を始点とする半直線が反時計回りに一定の角速度で回っているとします。例えば時計の長針は1分間で360度回るのだから,角速度は秒速6度です。ラジアン(\(\text{rad}\))で考えると,時計の長針は \(\frac{\pi}{30}\text{[rad/s]}\)の角速度で時計回りに回っていると考えます。
いま,反時計回りに半直線が角速度 \(\pi\text{[rad/s]}\) で回っているとします。秒速180度だから結構早いです。さらに,その回転している半直線の上を速度 \(1\text{[cm/s]}\) で動径方向,つまり原点から遠ざかる方向に動く点Pがあるとします。
半直線は時刻0で横軸の正の部分にあるとし,点Pは原点にあるとします。下図は,\(\frac{1}{8}\text{[s]}\)ごとに点Pの居場所を黄色の丸でプロットした図です。同心円の半径は \(\frac{1}{8}\text{[cm]}\) ずつ増えています。
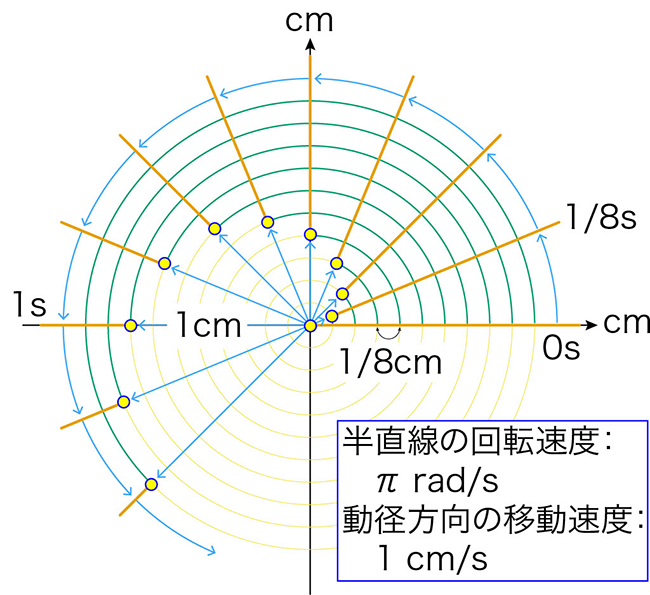
時間を無限に細かく刻んでいくと,黄色の点を通る赤い曲線が描かれます。
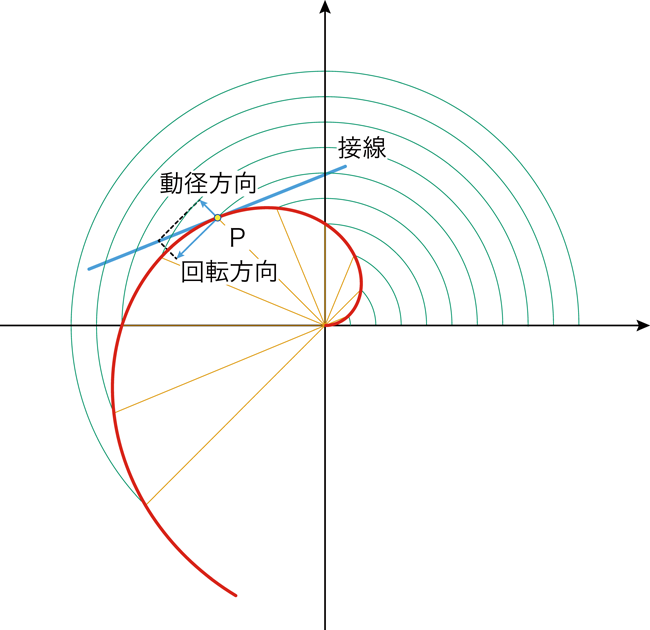
時刻 \(t\) 秒における点Pは,半径 \(t\text{[cm]}\) の円と,なす角が \(\pi t \text{[rad]}\) の半直線の交点です。
また,時刻 \(t\) 秒における点Pにおける速度ベクトルは,動径方向の速度成分 \(1 \text{[cm/s]}\) と回転方向,つまり半径 \(t \text{[cm]}\) の円の接線方向の速度成分 \(\pi t \text{[cm/s]}\) がなす長方形の対角線の方向です。
下図は,点P付近の拡大図です。
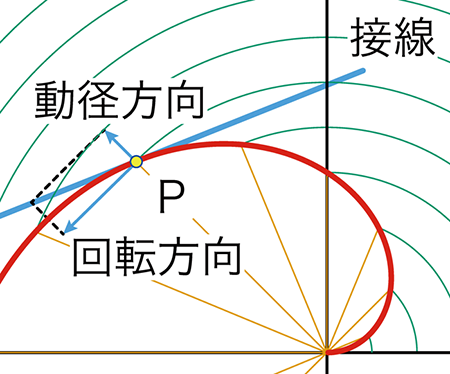
1秒後の点Pの位置は,半径1cmの円と横軸の負の部分の交点,つまり横軸の \(-1 \text{cm}\) の位置です。
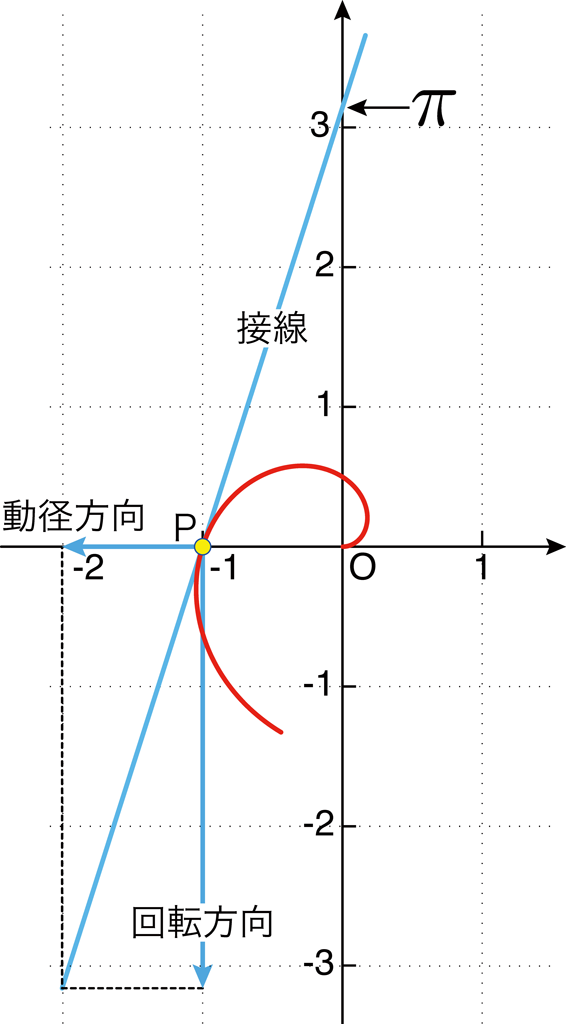
そのときの速度ベクトルは,横軸の負の方向に \(1 \text{[cm/s]}\) の動径方向の成分と縦軸の負の方向に \(\pi \text{[cm/s]}\) の回転方向の成分に分解されます。
そして,点Pにおける接線の方向は速度ベクトルに等しいから,接線と縦軸との交点の座標は \((0,\pi )\) となります。
アルキメデスはこうして長さの線分を構成しました。この赤い曲線は『アルキメデスのらせん』と呼ばれています。
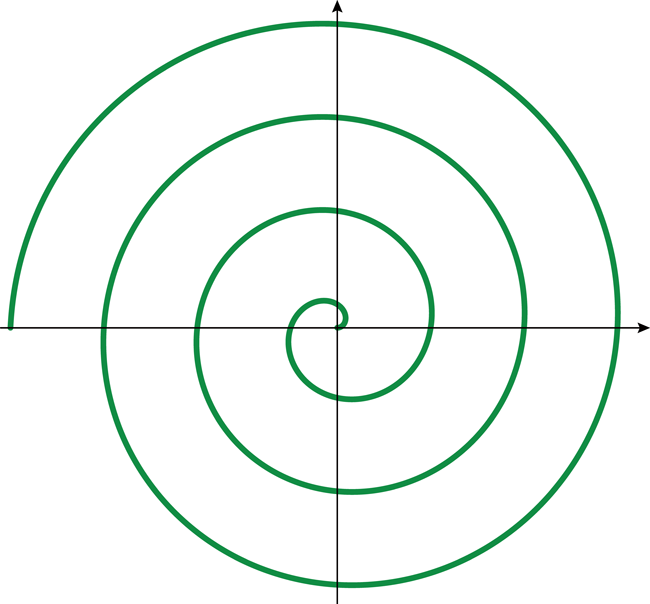
アルキメデスのらせんをもっと長く書くとこのようになります。

線を太くしました。

これは蚊取り線香です。

さらに,蚊取り線香は,パックに入っているときは陰陽を表す太極図のように点対称に配置された2つのらせんがぴったり重なって入っています。

アルキメデスのらせんもそれにならって点対称に配置して,それらしく見せるために,背景を蚊取り線香色にし,2つのアルキメデスのらせんは黒色にしました。
アルキメデスのらせんと蚊取り線香の形はよく似ていますね。
蚊取り線香は,着火すると外側から中心部に向かって,アルキメデスのらせんに沿って燻焼(くんしょう)が進みます。もしその燻焼速度が一定だった場合,角速度は,(1+偏角の2乗)の平方根に反比例することがわかります。だから,偏角が大きい蚊取り線香の外側の方が速度が遅く,中心部分に近づくにつれて進行速度が速くなるはずです。
※これは蚊取り線香の太さを無視した弧長の速度についての考察なので,より詳細には,太さを考えた面積速度や断面の形状も考えた体積速度の考察が必要です。
アルキメデスの贈り物
アルキメデスは紀元前250年ころに活躍した古代ギリシアの数理科学者です。あまりにも有名ですね。
功績は膨大です。直径1の円に内外から接する正96角形の周長を計算して円周率 \(\pi\) の小数点以下第2位までの値を3.14に確定したことは一つの業績に過ぎませんが,だいたい3.14ではなく,3.14までは正しいことを示したことは脅威的です。
アルキメデスの3.14から2000年後に円周率 \(\pi\) は無理数であることが証明されました(ランベルト,1761年)。
例えば \(\sqrt{2}\) が無理数であることの証明は \(\sqrt{2}\) が無理数でなかったと仮定して矛盾を導く背理法を使ったものが有名です。証明は数行で簡単に終わります。アルキメデスの50年前,紀元前300年頃にユークリッドが著書『原論』で示しました。一方,\(\pi\) の無理数性の証明は一筋縄では行きません。最短と思われるニーヴェンの証明(1947年)でもA4用紙1枚は必要で,ランベルトの証明は準備も含めてA4用紙数枚は必要です。しかしいずれも高校数学Ⅲか大学1年生くらいの数学の知識があれば理解できる初等的な証明です。
ランベルトからさらに120年後,\(\pi\) は有理係数の代数方程式の解にはならない超越数であることが証明されました(リンデマン,1882年)。このことは,\(\pi\) は定木とコンパスで作図できない数であることを主張しています。この主張は,ギリシアの三大作図問題の一つ『円積問題(円と等しい面積をもつ正方形を作図せよ)』を否定的に解決したことになります。
別の見方をすると,\(\pi\) が作図不可能である数であるという事実は,もし \(\pi\) を描くとしたら,円以外の曲線を使わなければならないことを意味しています。したがって,アルキメデスは定木とコンパスだけを用いた作図に固執せず,新しい曲線(アルキメデスのらせん)を使って作図のルールを弱めて『円積問題』を肯定的に”解決”したことになります。さすがのアルキメデスもらせんが蚊取り線香に使われることまでは想像していなかったでしょうね。
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
