茨城県立竜ヶ崎第一高等学校・附属中学校
小林 徹也 先生
(前編はこちら)
「あと5分」の発問例:「特殊な」場合
次に,「特殊な」場合である。
数学には,一般に成り立つ性質も特殊な場合には成り立たないことがある。またややもするとそれを見逃すことがある。
ここでは「特殊な」場合について説明(証明)させる生徒の状況に合わせた発問群を提案したい。
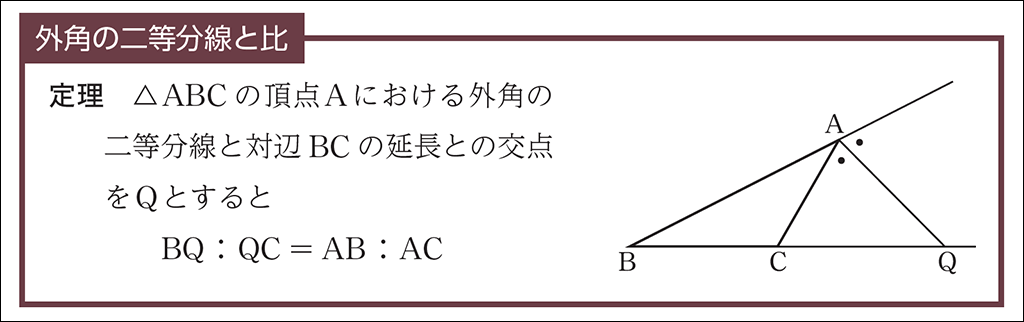
【発問0】\(\triangle \mathrm{ABC}\) が \(\mathrm{AB}=\mathrm{AC}\) の二等辺三角形のとき,点 \(\mathrm{Q}\) がとれないことを説明してみよう。
※「とれない」を「存在しない」と言い換えてもよい。
発問後の授業展開・生徒の反応
まず,上のように発問し,1分程度個別に活動させる。その後,発問群により複数のパートに分け生徒の考えを確認したい。
【発問1】「図をかいてみよう。」
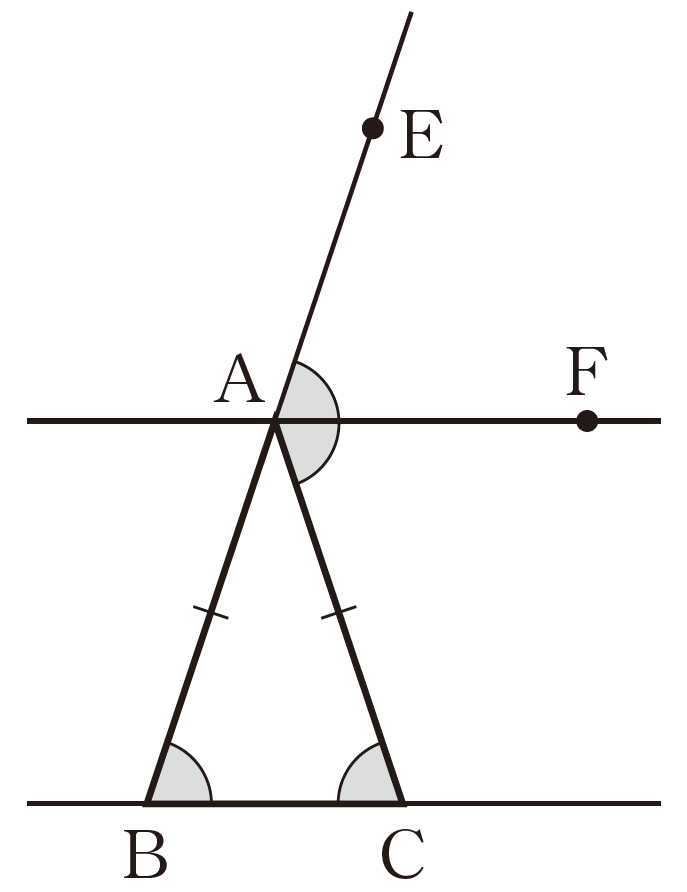
\(\mathrm{AB}=\mathrm{AC}\) だから,
\(\angle \mathrm{ABC}=\angle \mathrm{ACB}\) …①
\(\triangle \mathrm{ABC}\) の頂点 \(\mathrm{A}\) における外角 \(\angle \mathrm{EAC}\) の二等分線上に点 \(\mathrm{F}\) をとる。 …②
【発問2】「直線 \(\mathrm{BC}\) と直線 \(\mathrm{AF}\) は交わりそうか?」
すると,生徒は「描いた感じでは交わりそうにない。\(\mathrm{BC} /\!/ \mathrm{AF}\) ではないか?」と予想するだろう。
【発問3】「では,\(\mathrm{BC} /\!/ \mathrm{AF}\) を図と口頭で説明してみよう。」
\(\angle \mathrm{ABC}+\angle \mathrm{ACB}=\angle \mathrm{EAC}\) …③
すると,①,②,③より,
\(\angle \mathrm{ACB}=\angle \mathrm{CAF}\)
したがって,\(\mathrm{AF}/\!/\mathrm{BC}\)
ゆえに,\(\triangle \mathrm{ABC}\) の頂点 \(\mathrm{A}\) における外角の二等分線は辺 \(\mathrm{BC}\) の延長と交わらないから点 \(\mathrm{Q}\) はとれない。
【発問4】「この証明をきちんと書いてみよう。」
多くの場合,【発問3】までで十分だろう。余裕があれば【発問4】にあるように記述させてもよいだろう。
発問群の活かし方
上記の発問の説明(証明)の板書は前述【「あと5分」の発問例:「○○でない」場合】のような板書の修正より手間がかかるだろう。そこで,生徒に解答を発言させ,やり取りをしながら教師がポイントとなるところを板書すれば時間の短縮と正しい解答の説明の時間が確保できるだろう。
「あと5分」を活かすための発問群のヒント
最後にまとめとして次の提案をしたい。
- 問題を少し違った角度から見せるために既習の例題と比べて「○○でない」「特殊な」場合を考えさせる発問をし,さらに「発問群」により複数のパートに分け,確認する。
- 時短のために,板書・ノート・教科書等を部分的に修正させたり,考えさせたりする。または生徒が考えたその結果を発言させ,そのポイントを教師が板書する。
その他のコンテンツ
