特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

「個別最適な学び」と「協働的な学び」の一体的な充実を考える③

Q　「個別最適な学びと協働的な学びの一体化」を意識した単元の指導計画を考えています。単元の指導計画づくりでのポイントを教えてください。

Ａ　「個別最適な学びと協働的な学びの一体化」を意識した単元の指導計画を作成は、とてもよいことだと考えています。単元の指導目標にあわせた単元全体の問題解決の過程を考えることから始めてみましょう。

　前回は「個別最適な学びと協働的な学び」、特に「協働的な学び」を重視した中学校数学の授業づくりについてお話しました。今回は、授業場面だけでなく、内容のまとまりである「単元」の指導計画を考えます。例として、3年生の関数の指導場面について考えてみましょう。

□単元で重視する問題解決の過程を考える

　「新しい数学3」の3年の関数の指導は「第4章　関数の世界をひろげよう［ \(y=ax^2\) ］」に設定されています。東京書籍ウェブサイトに指導のための資料、「新しい数学　学習指導計画（略案）【3年】」が掲載されています。この資料を概観し、単元全体の生徒の問題解決の過程を考えてみましょう。指導内容として単元は3つの節に分けられており、さらに細かな内容が項として構成されています。下の表は単元の指導計画として、先の資料から抜粋し、「生徒の問題解決」を付け加えて作成したものです。【生徒の問題解決】をもとに、個別最適な学びと協働的な学びの一体化を考えてみましょう。

表　単元の指導計画と生徒の問題解決について

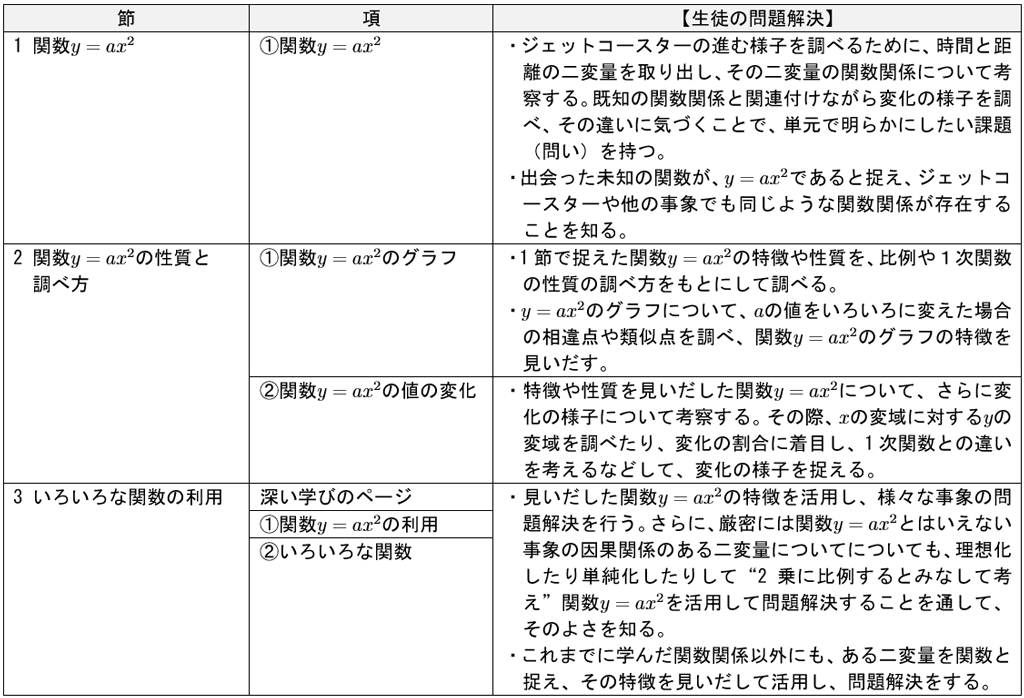
　【生徒の問題解決】を踏まえると、様々な場面で「個別最適な学び」と「協働的な学び」の場面を設定することができます。1時間の授業のなかで、個別最適な学びと協働的な学びの一体化考えることも大切ですが、章のようなある程度の時間のまとまりの中で設定することも大切です。
　例えば、2節2項では、\(y=ax^2\) の変化の様子について、生徒一人ひとりが特徴を予想したり、その予想を確かめる方法を考えたりする場面を取り入れることができます（個別最適な学び）。また、それぞれの生徒が見いだした特徴を、話し合って共有する場面を設け、理解を深めることができます（協働的な学び）。
　1時間ごとの授業を考えることも大切ですが、節や項などのまとまりで考え、いつどの場面で「個別最適な学び」と「協働的な学び」を取り入れるか、取り入れることで学びが深まるか、などを考えることも大切です。

□単元で重視する問題解決の過程を考える

　「【#2】数学の学習のスタート！〜単元の導入編〜」では、単元の導入で生徒が「単元の問いを持つこと」、単元の終末での「単元の問いに対する答えを示すこと」が大切であり、単元の指導ではその結びつきを重視したいことをお伝えしました。この単元でも同様に考えるとよいでしょう。「新しい数学3」p.93〜94では、ジェットコースターの進む（下りる）場合の様子を考察することで、既知の関数関係との違いに気づき、下のような“単元の問い”を生徒が持つことが予想されます。

　これらの生徒の「問い」を「学習課題」として価値付けることで、生徒一人一人が「自分が立てた学習課題」を解決することができます。自分で立てた学習課題だからこそ、生徒は主体的に取り組むことができるのです。
　このほかの問いを生徒が考えることがあるでしょう。問いは学級で一つにまとめる必要はありません。個人の課題としてもよいし、何人かの集団で追究していく課題としてもよいでしょう。

　こうした単元の学習課題（問い）を持つことが個別最適な学びの第一歩となります。生徒一人一人が持つ単元の課題を明らかにし、単元の学習を進めていく過程を大切にしてみませんか。

※参考資料

• 「令和の日本型学校教育」の構築を目指して～全ての子供たちの可能性を引き出す，個別最適な学びと，協働的な学びの実現～（答申）　令和3年1月26日（中央教育審議会）
• 新しい数学3（東京書籍）
• 「新しい数学」学習指導計画（略案）【3年】

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。