特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

文字式の計算を練習することに意味を持たせる指導（式の計算②）

Q　第2学年の「式の計算」では、教科書をみると文字式の計算についての問題がたくさん用意されています。それを計算し正誤を確認するだけの授業になってしまいがちです。こんなときの授業の進め方のポイントを教えてください。

Ａ　式の計算の単元では、知識及び技能の育成のために、文字式の計算に取り組む場面があります。学んだ文字式の計算のきまりをどのように適用させたかを振り返りながら取り組む場面を設定することが大切です。

　前回（#23）では、文字式の計算方法を学ぶ場面において、生徒が問いを持って計算のきまりを考える授業とすること、そして、そのポイントについてお伝えしました。教科書においては「Q」や「例」の後に「問」が設定されており、多くの計算問題が用意されています。指導される先生はこれらを適用問題として取り組む場面として設定すると思います。この場面で生徒の学習状況を把握し学習評価につなげるのではないでしょうか。しかしながら、この場面において生徒が計算に取り組み、その結果の正誤を確認するのみの時間になってはいないでしょうか。今回は、生徒が「問」を取り組む場面づくりの工夫について考えてみましょう。

□学んだ文字式の計算に関連づけて振り返る場面を設定する

　「問」として設定された問題について、授業の前に実際に先生ご自身でも解くと思います。その際、答えを確認するだけでなく、「Q」や「例」にある文字式と見比べてみてください。「Q」や「問」にある式の文字の種類や係数は異なるものの、式の構造は同じである問題とそうでない問題があることに気づくでしょう。
　例えば、新しい数学2、第1章「式の計算」（p.13）にある「例3」と「問4」にある問題をみてみましょう。「例3（1）」と「問4（1）」は同じ文字 \(x\)、\(y\) が使われ、係数が異なる式ですね。しかし、「問4（3）、（4）」は式の文字がこれまでと違うことや、\(ab\) といった文字どうしの積を含む項があります。しかし、同類項をまとめるという計算の進め方は同じですから、「例」と同じように計算すればよいと捉え、計算できるかどうかをみる問題になっているといえます。

新しい数学2 第1章「式の計算」 p.13

　こうした問題に取り組む際には、先生の関わり方が大切です。「問4」は学級全体よりも個人で取り組む場合が多いと思います。先生が正しい計算結果を答えとして示すだけでなく、生徒どうしで計算の結果を確認するのもよいでしょう。正誤の確認に加え、「例3」の計算との違いや共通点について振り返ることを促し、計算の方法や進め方についても生徒どうしで確認する場面を設定するとよいです。

□計算結果の誤りを確認し、それを正しい解答へ改善する場面を設定する

　多くの計算問題に取り組むことは大切ですが、計算のきまりや計算の方法を確認するために、誤った計算の例を用いて、正しく改善する場面を設定することも大切です。
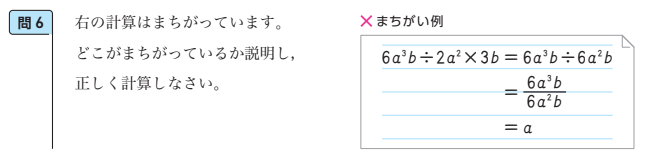
　例えば、新しい数学2、第1章「式の計算」（p.19）には、「まちがい例」から計算の間違いを指摘し、正しく計算する「問6」があります。

新しい数学2 第1章「式の計算」p.19

　この問を生かして、答えが正しくない原因を計算過程に着目して考える場面を設定します。この問題では、\(2a^2 \times 3b\) の乗法を先に計算したことで、正しい結果を導けなかったことを生徒どうしで確認することを促します。その上で、正しい計算結果と計算方法を見いだし、計算のきまりについて振り返り、理解を深めることができます。

　教科書に掲載された「問」などの多くの問題は、「Q」や「例」と関連させて考えることを促し、関連させて考えることで計算のきまりを確認し、的確に処理することができるようになります。また、「基本の問題」や「章の問題」にも多くの問題がありますが、これらについても生徒がつまずいた際に前の学習のどこに戻って考えればよいかについて、自身で考え、さらに前進できるようになる自律的に学びを進めていくことを期待したいです。

「生徒が文字式の計算を的確に処理することは大切ですか？」と問われたら、みなさんは、「大切です」とお応えになるのだと思います。どうして大切なのでしょうか。
　下のは、令和5年度全国学力・学習状況調査中学校数学大問2です。

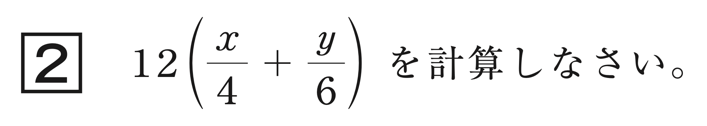
令和5年度全国学力・学習状況調査中学校数学大問2

　この問題は、数と整式の乗法の計算ができるかどうかをみる問題で、分配法則を用いて数学的に処理することが重視します。では、この文字式を正しく計算できることはどうして大切なのでしょうか。報告書（国立教育政策研究所,2023）には、下のような問題（例）と連立方程式とともに紹介されています。

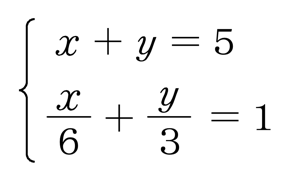
令和5年度全国学力・学習状況調査中学校数学報告書より

　上の連立方程式を解くためには、第2式において \(x\)、\(y\) の係数が整数になるように両辺を6倍して、分配法則を用いて処理します。つまり、問題の「大悟さんが歩いたそれぞれの道のり」を正しく知るためには、数学的に的確に処理することが必要なのです。
　式を数学的に的確に処理することができることで、真に問題解決に向かうことができるようになるのです。

※参考資料

• 新しい数学2（東京書籍）
• 令和5年度全国学力・学習状況調査中学校数学報告書（国立教育政策研究所）

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。