特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

図形の証明における指導を考える④ 〜アセスメント（学習評価）〜

Q　生徒が図形の証明を書くことだけでなく、証明を読むことも大切だと聞きました。その指導と学習評価について、何かポイントはありますか。

Ａ　次のポイントを意識してみましょう。

　前回は、証明を書くことができるようにするための指導とその評価として、生徒へのフィードバックについて紹介しました。図形の証明に関わる学習評価については、「「指導と評価の一体化」のための学習評価に関する参考資料」（国立教育政策研究所）に例示されています。第2学年2B(2)「図形の合同」には、下のような評価規準例について取り上げられており、前回は特に「三角形の合同条件などを基にして三角形や平行四辺形の基本的な性質を論理的に確かめたり･･･」について、具体の問題を例にしてお伝えしました。

　今回は、この後半部分にある「証明を読んで新たな性質を見いだしたりすること」を考えていきます。

□証明を読んで新たな性質を見いだすこと

　

　2年生の図形の証明では、「証明のすすめ方」を主に学習を進めていきます。その中で、予想した事柄を明らかにすることや、仮定と結論を明らかにすることについて学習します。その上で、仮定から出発し、既に正しいと認めた事柄を根拠にして結論を導くといった「演繹的に考察する数学的な推論」を大切にして授業されていることと思います。証明について、生徒は“書くもの”と捉え、教師は“正しく書くこと”に注力している場面をよく目にします。しかし、中学校学習指導要領（平成29年告示）解説数学編には、「証明を読んで新たな性質を見いだすこと（イの（ア））」も設定されています。
　このことについて、具体的な問題として平成30年全国学力学習状況調査中学校数学B4(1)をみてみましょう。

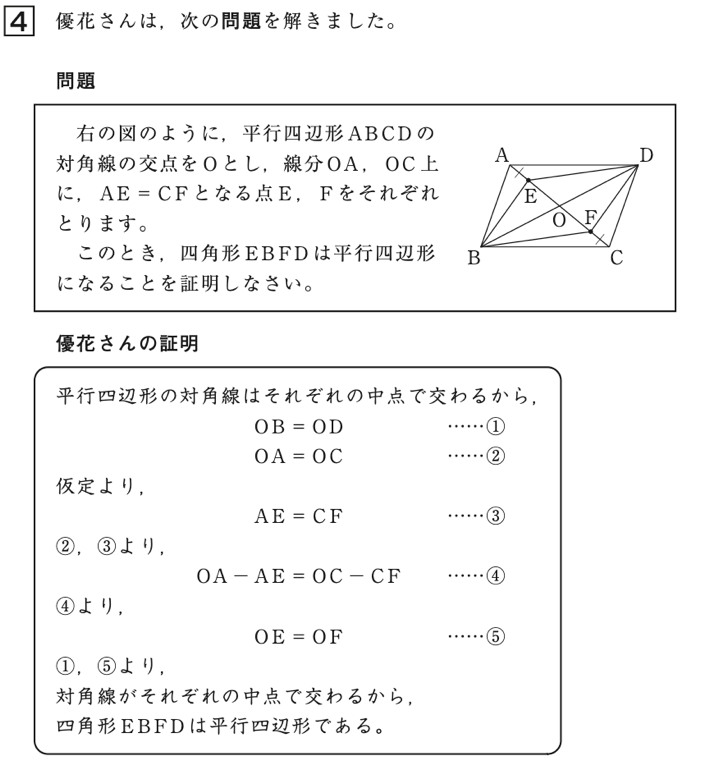
平成30年度全国学力・学習状況調査中学校数学B4(1)

　この設問は、「証明を振り返り、証明された事柄を基にして、新たな性質を見いだすことができるかどうかをみる。」を趣旨としたものです。正答はアで、正答率は56.0％でした。四角形 \(\text{EBFD}\) が平行四辺形であることが証明されたことを受けて、平行四辺形の性質と関連付けて考え、見いだすことを評価します。誤答として、ウを選択している生徒が25.3％でした。このような生徒は、\(\text{OE}=\text{OF}\) が、四角形 \(\text{EBFD}\) が平行四辺形であることを証明することに用いられている根拠であることを捉えることができなかったのではないかと報告書では分析されています。書かれた証明が「仮定から出発し、既に正しいと認めた事柄を根拠にして結論を導いている」と解釈することができず、困っている生徒かもしれません。証明を書いた後に、証明を読むことで振り返り、教師が「何か新たにいえる図形の性質はないだろうか」と問うてみるとよいでしょう。証明を読むことは証明を吟味し、さらには証明をもとに発展的に考えることにつながる大切な活動です。
　証明を振り返り、新たな性質を見いだすことについて、教科書を見てみます。新しい数学2 p.131には、下のような学習場面が設定されています。

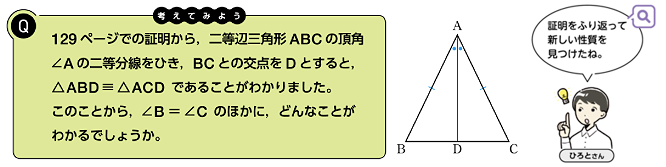
　ここでは、\(\triangle \text{ABD}\) と \(\triangle \text{ACD}\) が合同の関係になることを基に \(\angle \text{B}=\angle \text{C}\) が成り立つこと（二等辺三角形の底角は等しい）を示した証明を振り返り、新たな性質を探すといった探究的に考察を進める場面です。二等辺三角形の性質として「頂角の二等分線は、底辺を垂直に2等分する」を見いだすのですが、書かれた証明を出発点とし考察します。二等辺三角形や平行四辺形の考察では、このような、既に証明されたことをもとにして図形の性質の考察することが続きます。教科書、特にQでは、ある命題の発見を次の命題の発見につなげることについて促しているのではないかと思います。

　2年生以降の図形の学習において、成り立つと予想した事柄を証明する活動、さらに、その証明をもとに新たな図形の性質を見いだす活動へと考察がつながり、図形の性質について探究的に学ぶことができるような授業が大切です。また、証明を正しく書ければよいということでなく、生徒が数学的推論を働かせて問い続け、図形の性質を考察し続けることを授業づくりの視点としてみてはいかがでしょうか。

　4回にわたって、「図形の証明」をテーマに考えてきました。生徒にとって図形の授業が、楽しい考察の時間とするために、生徒が論理的に考えることを重視し、その評価を充実させていくことが大切です。

※参考資料

• 「指導と評価の一体化」のための学習評価に関する参考資料
• 中学校学習指導要領（平成29年告示）解説数学編
• 平成30年全国学力・学習状況調査中学校数学調査問題
• 平成30年全国学力・学習状況調査報告書中学校数学

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。