特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

図形の証明における指導を考える② 〜方針や構想を立てること〜

Q　図形領域の単元が始まり、証明についての指導で悩んでいます。生徒はなかなか証明を書くことができません。証明することができるようになるための授業づくり、授業でのポイントはありますか。

Ａ　次のポイントを意識してみましょう。

　前回は、証明の必要性と意味について、どのような授業で指導をするかということを取り上げました。今回は実際の授業づくりについて、特に「証明する活動を取り組む際に見通しや構想を立てる場面を取り入れる。」ことを考えてみましょう。

　まず、中学校学習指導要領（平成29年告示）解説数学編を確認します。中学校数学で育成する3つの資質・能力のうち「思考力・判断力・表現力等」は下のとおりです。

　論理的に考察する力として、数学的推論（帰納、演繹、類推）が取り上げられますが、中学校数学では、問題解決の際に演繹的に推論することが多くなります。図形の証明はその1つであろうと思います。生徒が証明することができるようにすることは大切ですが、授業において証明を書く場面に偏ってしまい、書き方の指導となってはいないでしょうか。

□授業に証明の方針を考える場面を設定する

　図形の証明を行う授業をみておりますと、問題を確認し、先生が「それでは証明してみましょう」と発問し、証明を書くという場面をみます。ここで、なかなか自分では進めることができない生徒をみて、「“仮定と結論”を確認しましょう」と発問し、みんなで確認します。それでも、証明を書くことができない生徒もいます。もちろん、“仮定と結論”を確認することで何を示そうとしているかを明確にするものですので、大切な問いかけです。しかし、証明を書くことができない生徒の多くは、どのように導いていけばよいかという説明する筋道がわからなくて困っているのではないでしょうか。
　下の紙面は、新しい数学2 p.129にある「二等辺三角形の底角は等しい」ことを証明する箇所の冒頭にあるものです。小学校3年生において、二等辺三角形の2つの角が等しくなっていることを、二等辺三角形の紙を折ることで確認しています。単なる算数の復習とするのではなく、二等辺三角形の紙を折ることについて辺や角の関係に着目して振り返ってみましょう。折り目の線により頂角が2等分され、2つの合同な三角形ができることなどを確認する場面を設定することが考えられます。

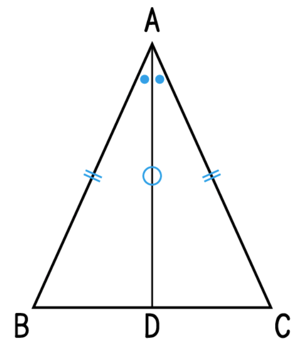
　その上で、「どんな二等辺三角形でも２つの角は等しくなるといってよいか」を問います。ここで「\(\text{AB}=\text{AC}\) の \(\triangle \text{ABC}\) ならば、\(\angle \text{B}=\angle \text{C}\) になる」という事柄に表し、この証明を「算数で二等辺三角形を追って底角を重ねた学びを活かして進めることができないか」と促します。すると、下のようなことを学級で共有することができます。

• \(\angle \text{B}=\angle \text{C}\) を示すためには、\(\triangle \text{ABD} \equiv \triangle \text{ACD}\) をいえばよい。
• \(\triangle \text{ABD}\equiv \triangle \text{ACD}\) を示すためには、三角形の合同条件のうち1つをいえばよい。
• 二等辺三角形の紙を折ったときの線は頂角である \(\angle \text{A}\)の二等分線になる。

　これらを確認した上で、証明を書く活動を個人やグループで取り組みます。先生は、生徒が書いた証明について、根拠を示して説明しているかどうかを見とり、適切に声をかけていくことが大切です。また、書いた証明を確認する際には、学級みんなで立てた方針と関連させて振り返ることも大切です。こうした経験をもとに、自分で証明を考える際にも、方針や構想を立てて証明に取り組むのではないかと思います。

　今回は、証明を実際に書く前に、方針や構想を立てるということを紹介しました。2年生での図形証明は、いわば論証の入門期といってよいと思います。こうした活動を最初は学級みんなで、そして、個人でなど形態を工夫しながら、成り立つと予想した事柄をどのようにすれば説明できるのかについて考えるが大切です。

※参考資料

• 中学校学習指導要領（平成29年告示）解説数学編
• 東京書籍 「あたらしい算数3上」
• 東京書籍 「新しい数学2」

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。