特集記事（小中学校）

　前の学習とつなぐ。次の学習へのつながりをつくる。今も昔も変わることなく、先生方が大切にされてきた価値観です。
　「新編 新しい算数」では、「今日の学習を次の学習へつなげる」ために、新しく「それなら」というキーワードを紙面に付記しています。

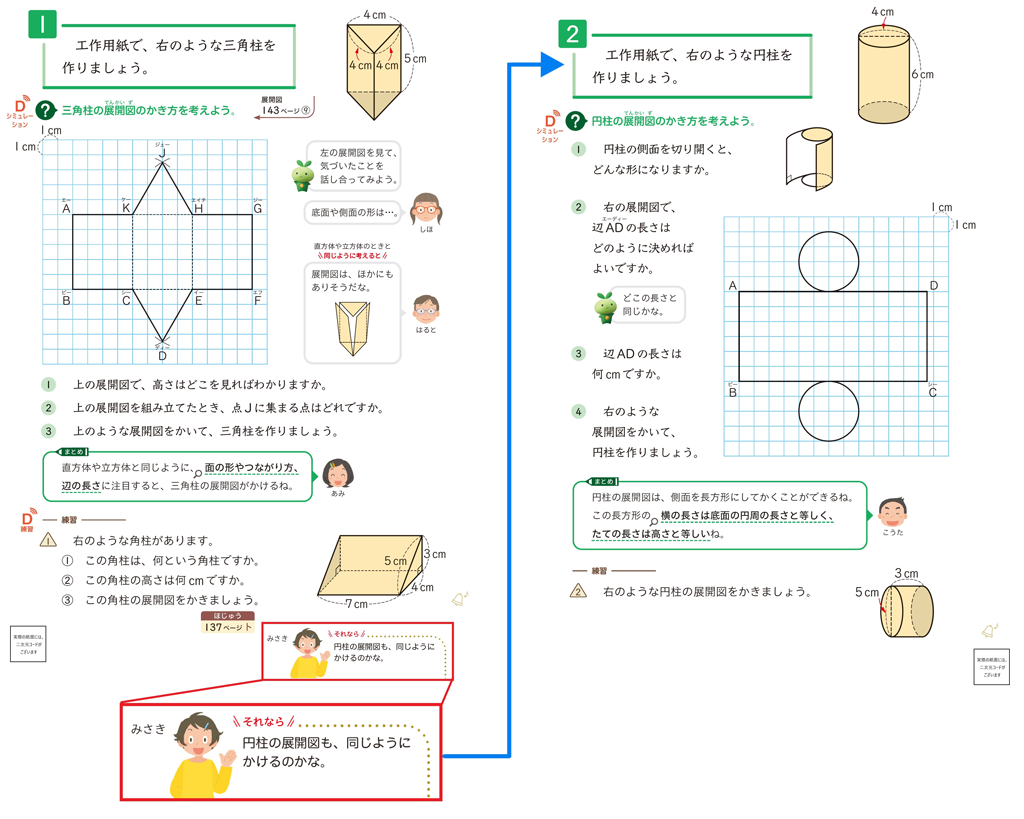
　5年下の「角柱と円柱」では、角柱の展開図のかき方を考えた後に、同じように図形の構成要素に着目して考えれば、円柱の展開図もかけそうだと、発展的に学びをつなぎます。

　第5時（p.116）では、図形の構成要素に着目して、角柱の展開図の作図方法を考えます。まとめとして、4年での直方体や立方体の展開図と同じように考えると、角柱でも面の形やつながり方、辺の長さに着目すれば作図できることを統合的にとらえます。締めくくりに「それなら円柱の展開図も同じようにかけるのかな」という次時の学習をつくり出す児童の姿を例示しています（みさき吹き出し）。

　このように、学習したことを基に「それなら○○の場合もできそうだ」と発展的に考えることで、学びがつながるとともに、自ら課題を見出し解決する力が育つと考えます。