特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【特集】つなぐ・つながる学び① ~前の学習と今日の…
前の学習とつなぐ。次の学習へのつながりをつくる。今も昔も変わることなく、先生方が大切にされてきた価値観です。
「新編 新しい算数」でも大切にしている「つなぐ・つながる学び」をご紹介します。今回は、計算領域における「前の学習と今日の学習のつながり」に注目します。
計算の仕方を考える際に働かせる見方・考え方のひとつに、もとにする数の何こ分かに着目して、計算するというものがあります。この見方・考え方の価値を実感し、前の学習と今日の学習をつなぐ力を育てたいです。
1年②「あわせて いくつ ふえると いくつ」では、初めて加法を学習します。ここでは、ブロック操作をしながら加法の意味を理解していきます。
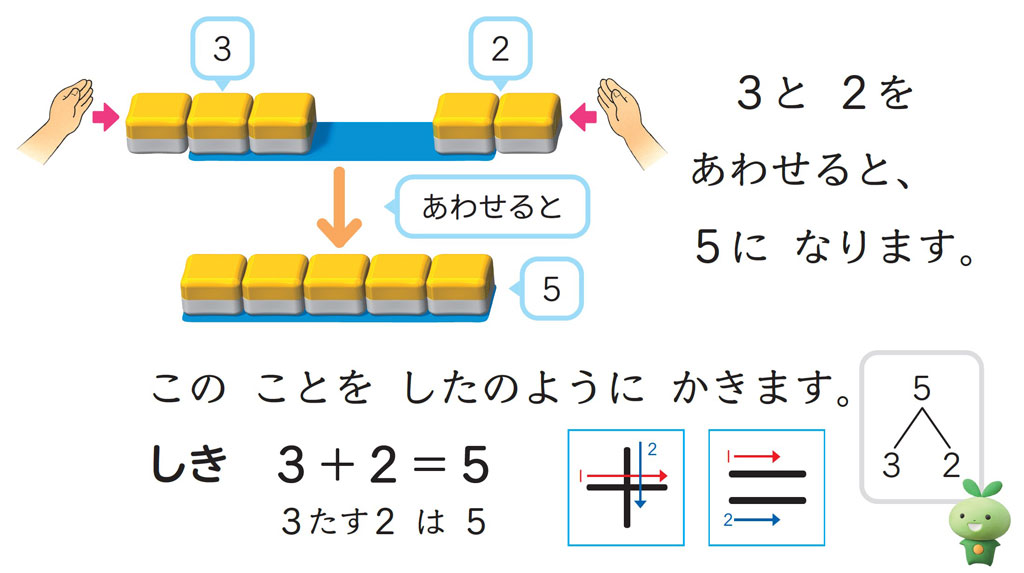

1年②「おおきい かず」では、何十 \(+\) 何十の計算を考えます。もとにする数の何こ分かに着目して計算するのは、ここが初めてですが、1年生なりの表現で「10のたばでかんがえると、3こと2こだから…。」と考えることを促しています(こうた吹き出し)。 次に何十 \(-\) 何十の計算を考えますが、加法と同じ見方・考え方を働かせることを促し、解決に導いています(あみ吹き出し)。

10をもとにして、既習の計算に帰着させて考える

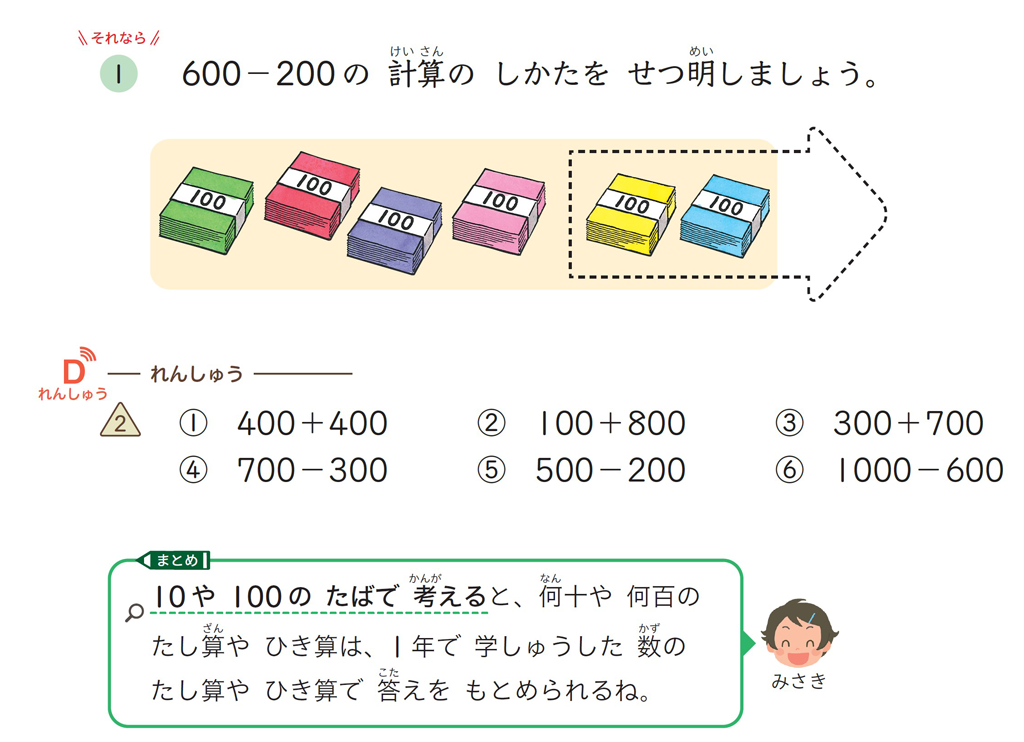
2上「3けたの 数」で、\(300+200\) の計算を考える際には、何十 \(+\) 何十の計算の仕方を想起させ、もとにする大きさに着目し、既習の計算に帰着して考えることを促しています(しほ吹き出し)。また、次の \(600-200\) では、少しステップアップして計算の仕方を説明することで、100のたばの何こ分で考えるという計算の仕方の理解を深めることを意図しています。
まとめでは、見方・考え方をしっかりと価値づけ、1年の学習と統合しています。
学年をまたいで学びをつなぎ、もとにする大きさに着目して計算することの価値を実感しながら、以後の学習においても同じように考える力を伸ばすことを目指しています。

100をもとにして、既習の計算に帰着させて考える
100をもとにして、既習の計算に帰着させて考える

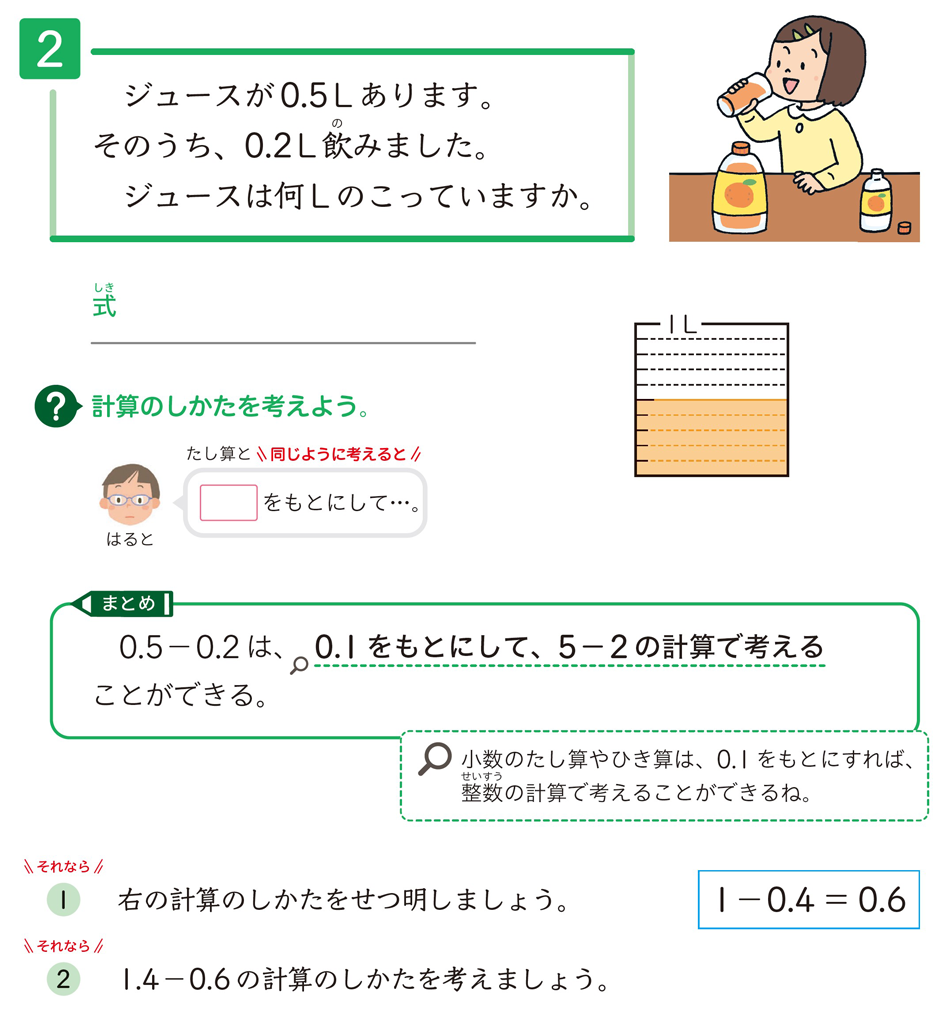
3下「小数」では、\(0.3+0.2\) の計算を考え、小数の計算でも整数の計算と同じ見方・考え方を働かせることを実感し、あらためて価値づけます。 次の \(0.5-0.2\) の計算を考える際には、児童が自覚的に同じ見方・考え方を働かせることを促しています(はると吹き出し)。

0.1をもとにして、既習の計算に帰着させて考える
0.1をもとにして、既習の計算に帰着させて考える

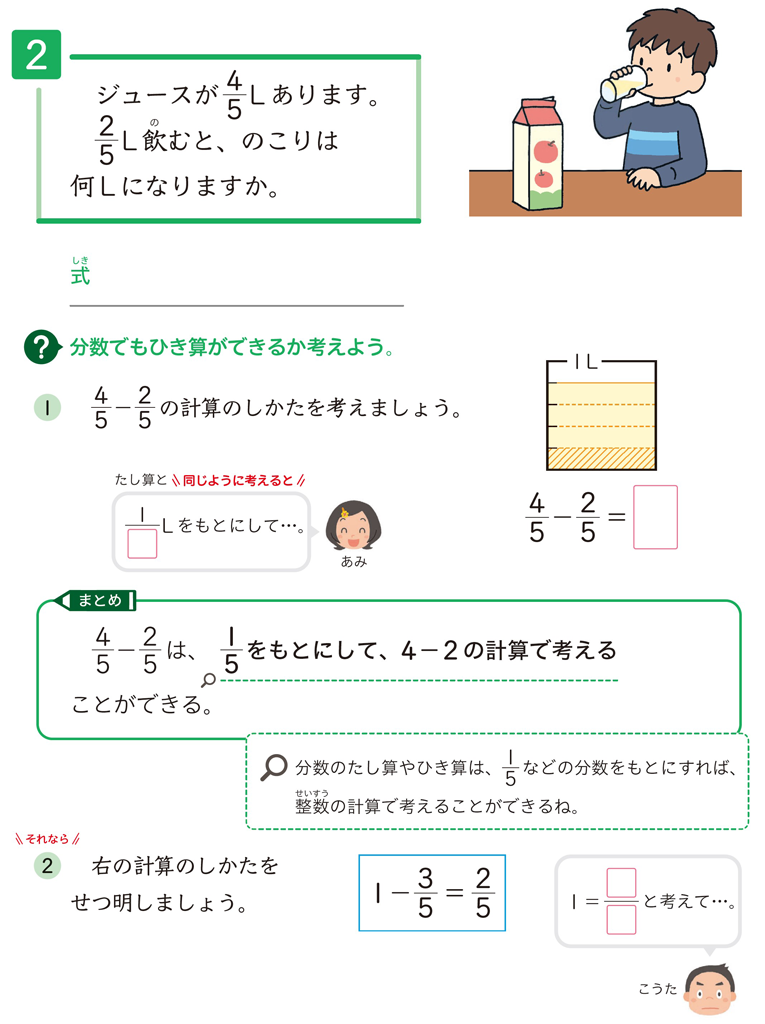
さらに、3下「分数」でも、\(\dfrac{3}{10}+\dfrac{2}{10}\) や \(\dfrac{4}{5}-\dfrac{2}{5}\) の計算を、これまでの学習と同じように考えて解決していきます。この段階では、整数や小数と同じように考えられそう、という気づきを児童から引き出し、前の学習とのつながりを意識させたいと考えます(3下p.53みさき吹き出し、3下p.54あみ吹き出し)。
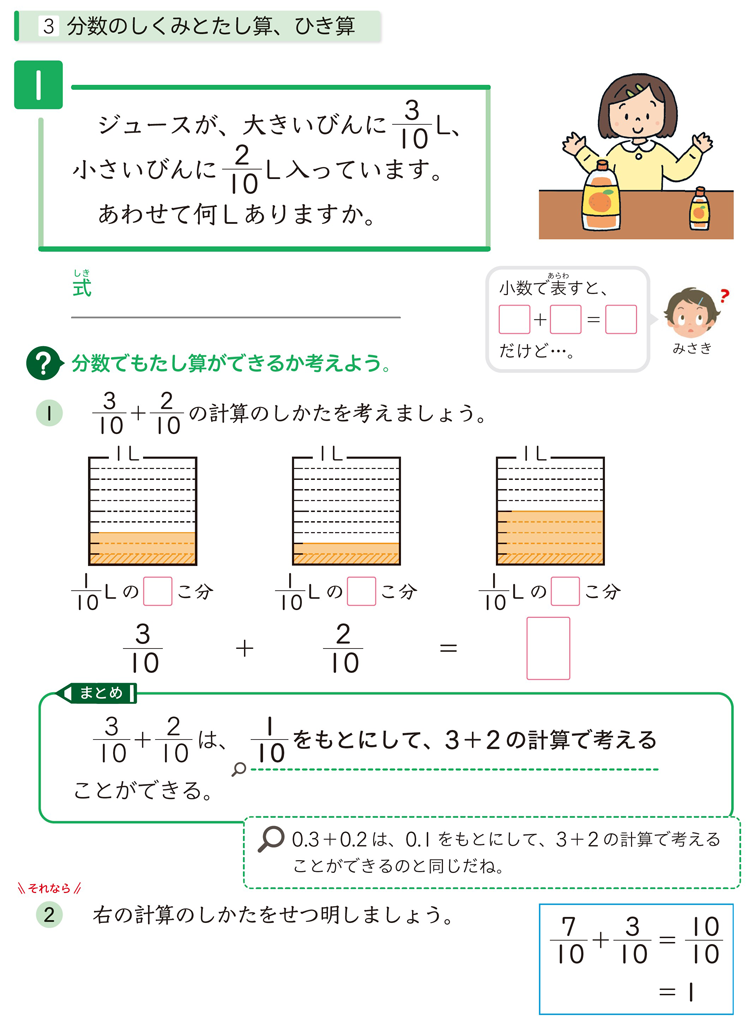
\(\frac{1}{10}\) をもとにして、既習の計算に帰着させて考える
\(\frac{1}{10}\) をもとにして、既習の計算に帰着させて考える
ここで、1年から3年の加法の式を振り返ってみると、「\(3+2\)」→「\(30+20\)」→「\(300+200\)」→「\(0.3+0.2\)」→「\(\dfrac{3}{10}+\dfrac{2}{10}\)」となっていて、どれも「\(3+2\)」の計算に帰着して考えることができます。
「新編 新しい算数」では、前の学習と今日の学習のつながりを実感しやすいように、見方・考え方に加えて、数値も統一して提示しています。
その他のコンテンツ
