特集記事（小中学校）

国立大学法人岩手大学
准教授　佐藤寿仁先生

　数学的に考える資質・能力を育成するためにどのような授業が求められているでしょうか。4月19日に実施された全国学力・学習状況調査中学校数学の問題を取り上げ、授業づくりのポイントを紹介する第2弾です。

　令和4年度実施の全国学力・学習状況調査中学校数学大問6(3)を取り上げます。

※問題はこちら　https://www.nier.go.jp/22chousa/22chousa.htm

POINT①：事柄について条件を変えて考え、探究的に生徒が考察する場面を設定する

　この問題は、2つの偶数の和について、「同じ2つの偶数の和は、4の倍数になる」「差が4である2つの偶数の和は、4の倍数になる」ことを説明した後に、同じように4の倍数になるものとして、どんな2つの偶数があるかについて考え、それを成り立つと予想される事柄として解答する問題です。4の倍数になるという結論部分を変えずに、前提となる2つの偶数がどのような偶数なのかを考察することは、統合的・発展的に考えることであり、生徒の数学的な見方・考え方を豊かにする場面となります。
　実際に生徒が考える際には、次のような活動を設定することが考えられます。

・帰納的に考えることで成り立つと予想される事柄を見いだす

　調査問題では「\(2+6=8\)、\(4+6=10\)、\(6+6=12\)」まで記載されているが、この後の続きを実際に書いてみることで、和が4の倍数になる例を取り出し、共通していることはないかと問うことで、生徒が見いだすことができると考えられます。いろいろな例からきまりを探すといった小学校算数からの学習経験を大切にするとよいです。生徒によっては、思いつくまま2つの偶数の和を考え、共通することを見いだせないということもあります。そのような場合には順序よく並べるなど整理して考えることを促すとよいでしょう。文字の使用にこだわらず、予想する場面では、具体的な数を用いて考えることは大切です。

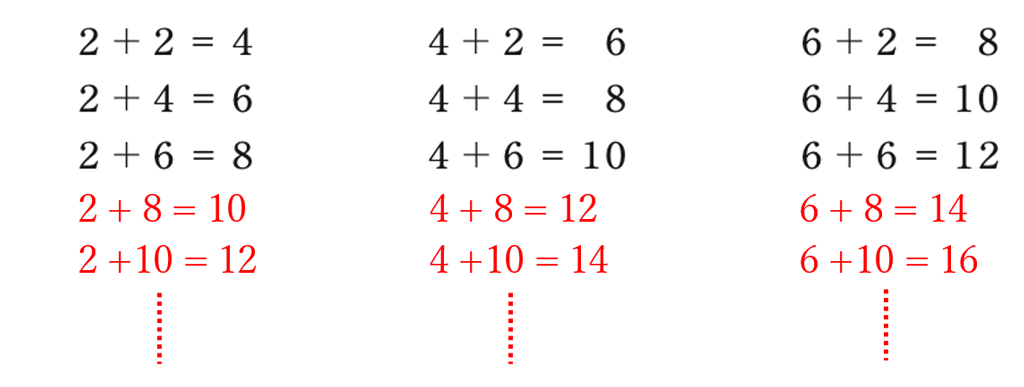
※全国学力・学習状況調査より

・書いた説明を振り返ることで成り立つと予想される事柄を見いだす

　2つの偶数の和について、「同じ2つの偶数の和は、4の倍数になる」「差が4である2つの偶数の和は、4の倍数になる」について説明を振り返ることも考えられる。例えば、4の倍数になることを説明するためには、式を「\(4×\)（整数）」と表すことが必要ですが、計算された文字式を4で括るためには、4、8、12、16などの数になればよいと考えることが予想されるのです。

※全国学力・学習状況調査より

POINT②：統合的・発展的に考える場面を設定する

　全国学力・学習状況調査の問題は問題そのもののインパクトだけでなく、学習指導要領で大切にしていることについて具体的に示すことがあります。本問は、統合的・発展的に考えることの一例であると考えられます。

（1）では、「同じ2つの偶数の和は、4の倍数になる」、（2）では、「差が4である2つの偶数の和は、4の倍数になる」、（3）において、仮に「差が8である2つの偶数の和は、4の倍数になる」と予想し、成り立つことを説明したとします。このとき「他にはあるかな？」と発問すると、差が12や16などのときと答えるでしょう。生徒はこの事象を統合的・発展的に考えようとしているといえます。

さらに、複数の事柄について、「一つにして考えることはできないか？」と問うことも考えられます。事柄の前提に着目し、差が4、8、12、16などを4の倍数といった一つの集合としてみることができるということに気づき、「差が4の倍数である2つの偶数の和は、4の倍数になる」と事象の本質を見極め表現するでしょう。このことが統合的・発展的に考えたことになります。

なお、「同じ2つの偶数の和」についてはどう考えるのか、と問うことも大切です。「同じ2つの偶数」を「差が0の2つの偶数」とみれば同じように考えることができるなどと説明し、さらに統合するということになるのです。

POINT③：教科書を活用して、統合的・発展的に考えることができる授業を構想する

　統合的・発展的に考えることを特別なこととして捉え、普段の授業では難しいとお考えになる先生はいませんか。例えば、教科書p.23、24をみると予想した事柄を説明した後にさらなる問いに挑戦するようなものが掲載されています。

　これらは、与えられた問題の条件を変えて数に関する性質をさらに追究していくというものであり、統合的・発展的に考える場面である。条件を変えることで、事柄の結論部分が変わらず統合的に考えることができることもあるでしょう。また、条件を変えることで新たな性質を見いだすことができるということもあるでしょう。こういった場面を授業に取り入れることで、数学的な見方・考え方が豊かになっていくものと考えられます。授業だけでなく、レポート課題として個々で取り組むこともよいです。