特集記事（小中学校）

「主体的・対話的で深い学び」を実現するために、教科書をどう読み解き、授業づくりに活用していけばよいのでしょうか。
今回は、第2学年「データを比較して判断しよう」を取り上げ、お二人の先生に、教科書を活用した学びのデザインについてお話しいただきます。

箱ひげ図の導入では、生徒の必要感を大切にする

―今回学習指導要領で新たに追加された「箱ひげ図」は、多くの先生方も学んだ経験がありません。どのようなことを意識して指導することが求められますか。

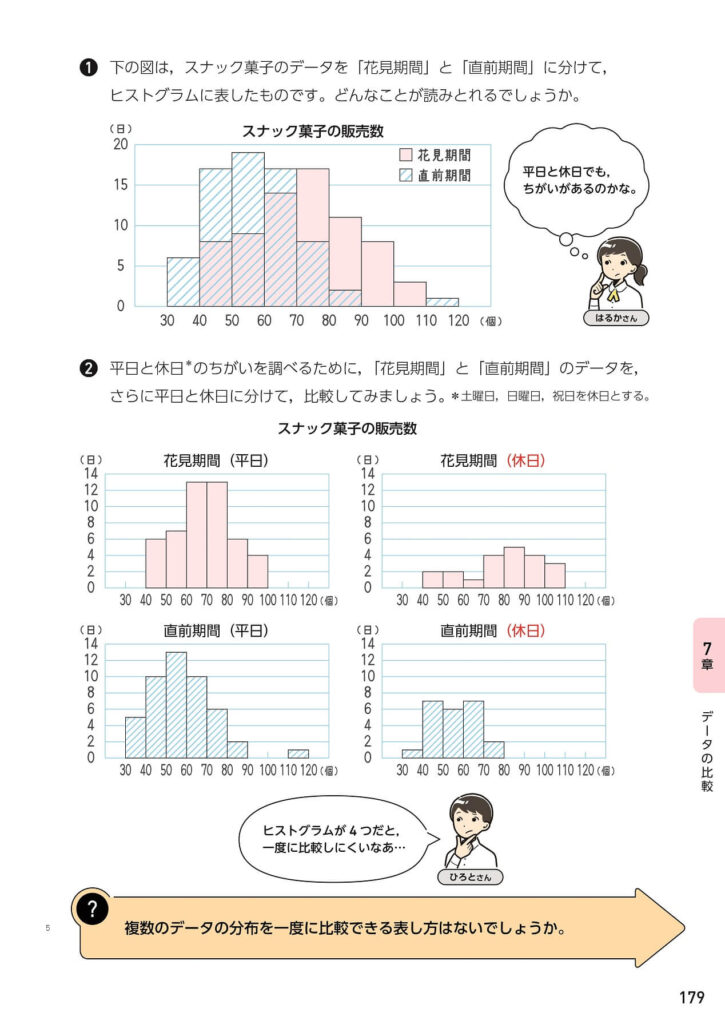
佐藤　箱ひげ図だけに限りませんが、新しい内容を指導する際には、それを学ぶ必要感や意義を大切にしたいですね。箱ひげ図の単元の導入においては、複数のヒストグラムを一度に比較しづらいことを生徒が実感することにより、箱ひげ図を学ぶ必要感を持たせたいと考えます。

小岩　私は初めて箱ひげ図を指導することになりますので、未習である生徒の気持ちになって教科書を最初から読んでみました。その中で、p.179 の4 つのヒストグラムが大切だと感じました。平日の「花見期間」と「直前期間」のように2 つのヒストグラムを比較することはできますが、休日も含めた4 つのヒストグラムとなると、分布の様子などを同時に比較することは難しい。このことを生徒に実感させたいと思いました。そのためには、「この4 つのヒストグラムを比較したい」と考える動機づけが大切だと考えます。

佐藤　p.178 の生徒の吹き出しに「販売数を比べれば…」とあります。実際の授業ではこの部分を扱ってほしいと考えます。生徒が「販売数を一度に1つの図で調べたい」「販売数の散らばりについて調べたい」という考えを持てると、4 つのヒストグラムを比較する流れをつくることができると思います。

小岩　そうですね。データの活用では、統計的探究プロセスPPDAC のProblem（問題）が重要だと考えています。授業では最初に「店長は、よく売れる商品を調べたいこと」を共有します。その上で、「どうする？」と生徒に投げかけることで、生徒は自分事として考えられるようになり、それがPlan（計画）につながります。そして、「どんなデータがほしい」「なぜそう思うのか」などと問えば、p.178 のような生徒のやり取りができると思います。こうしたProblemとPlan の活動を大切にすれば、どう調べればよいかは自然と出てくるのではないでしょうか。

 佐藤　統計的にデータを分析するときには、どんな手法で、どの変量に着目して調べるのかという
ProblemとPlan の間を大切にしたいです。問題発見・解決の過程の図でいう焦点化です。ヒストグラムでは縦軸と横軸がありますが、箱ひげ図は軸を減らして考えています。調べたい事柄や分析の目的を、横軸の内容に焦点化しないと、箱ひげ図を使って分布を調べる流れにはなりにくいのではと感じています。

小岩　箱ひげ図を実際にかいてみると、分布は意識しやすいけど、データの個数は意識しにくくなると感じました。箱やひげの長さをデータの個数と勘違いする生徒が出てくるのは、軸が減ることが影響しているのかもしれませんね。

 佐藤　調べる数量を意識しないと、解決の流れの中で何を分析しようとしているのか、生徒は混乱してしまうかもしれません。それぞれの段階で丁寧に発問して授業を進めたいですね。たとえば、教科書では「～を調べてみましょう」とありますが、「～のために～を調べてみましょう」と「～のために」を意識して発問することも考えられます。

小岩　調べる目的を意識させることは、目的にあわせて統計手法を選ぶことの理解にもつながります。文脈の中で、目的に応じて道具を選び問題を解決するという経験を積ませたいところです。

佐藤　私もそのように考えています。指導される先生もこのような経験が少ないので、生徒と一緒に考え、統計的な問題解決をするという立場で授業づくりに取り組んでほしいと思います。

生データの観察を取り入れた授業づくり

―p.190 以降にすべてのデータを表にして掲載しています。先生はこのデータを授業でどのように扱いますか。

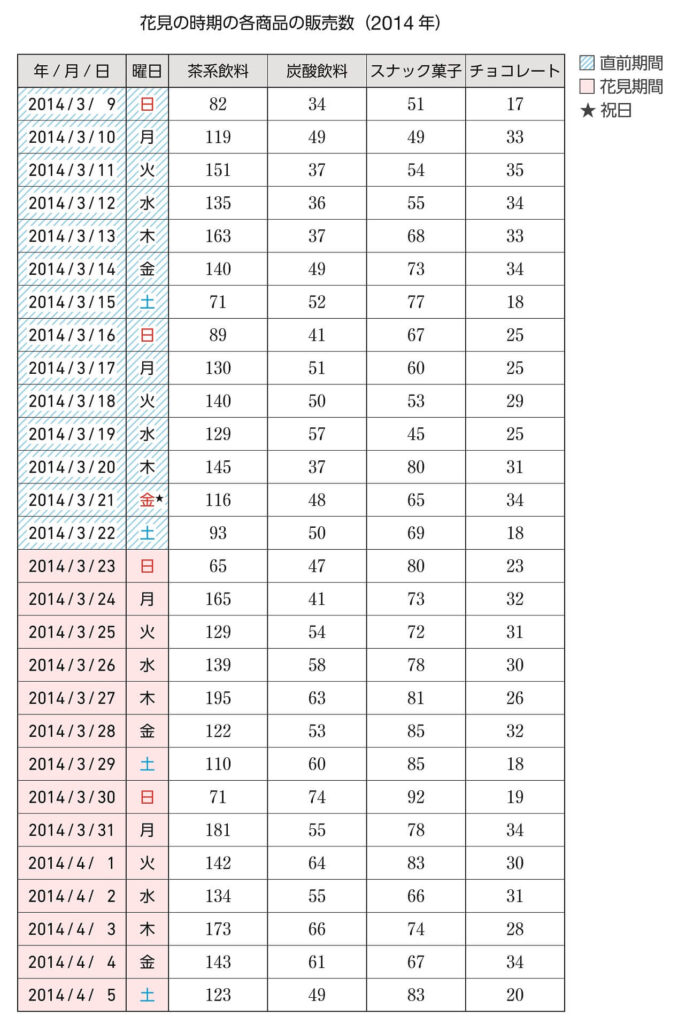
小岩　初めにこの表を見せ、「どの商品が売れたのかな」と予想を立てる場面を設定します。そうすると、生徒は「茶系飲料は週末少ない」などと気づくと思います。そこで、「わかりやすく表現する方法はない？」と聞けば、ヒストグラムを使う考えが出るのではないでしょうか。

 佐藤　このデータは、膨大なリアルデータであるということがよいですね。だからこそ、生徒は自分で整理して考えてみたいと思うのではないでしょうか。その向かう気持ちを掻き立てることができるかどうかが、我々教員の仕事ですね。

小岩　その後の問題解決を意識して、生データを観察させたいですね。「どの商品がよく売れたのか」、「休日と平日で違うのか」、「花見期間かどうか」などをPlan（計画）として出させておくと、その後の活動がスムーズになると思います。

 佐藤　そのように考えると、p.178 は盛りだくさんにも思えます。しかし、データを見つめながら1時間かけて考える価値があるところです。

小岩　「データが多すぎてわからないよ」という声が生徒から出てきそうです。

 佐藤　そうです。その言葉が出てきたら、すかさず「では、どうしたい？」と聞きたいですね。そのようなやり取りで授業を進めてほしいと思います。
p.190 の表を示すと、その表のみをずっと見て、データの傾向を見出そうとする生徒はいませんか。

小岩　いると思います。その生徒が見つけたことが、後で分析の観点に繋がってくるはずです。それが面白いところですね。

 佐藤　この表だけでは傾向の判断がしにくいと思うので、予想した傾向を調べることを目的にして分析するのもよいと思います。また、分析した後に、表を振り返って予想の正しさを確認できると面白いですね。

指導の経験がないからこそ生徒の立場に立った授業デザインを

 佐藤　教科書の箱ひげ図の章は、指導計画として何時間を想定して作られているんですか。

―本文が4時間、章の問題が1時間です

 佐藤　本当はもっと時間をかけたいですね。統計的探究プロセスは、小学校算数、中学校第1学年での経験を踏まえ、生徒自ら緩やかに回しながら問題解決をすることができるようにしたいです。

小岩　そうですね。授業を考えるときは、生徒の立場に立って、生徒だったらどう考えるのかを想定しておきたいです。

佐藤　サイクルというと一方向にのみ進むと考えがちですが、実際の授業では、サイクルを行ったり来たりすることがよくあります。学び方を生徒の立場で考えると、生徒の発する問いに授業の進行を委ねることも大切です。そうすることで、授業の進行も寛容になれると思います。統計は答えが１つに定まらな
いこともあります。社会に出たら正解を1つ選択することだけでなく、よりよいと考えられる答えを導き、判断しなければならないことも多くあります。こういう経験をしてほしいですね。
箱ひげ図は、先生自身も授業を受けた経験がなく、それを参考に考えることが難しいです。ぜひ、生徒の立場に立って問題解決するという視点で、授業づくりを考えてもらいたいと考えています。

小岩　指導の経験がないからこそ、教科書の流れを参考にしてほしいです。店長の気持ちになって考えると、「花見の時期に売上を上げたい」「何を調べたらよいか」「天気や気温は売上に関係があるのか」など素朴に考えてデータを用意しなければならない。教科書の活動を実際に経験しながら、教材研究を深めていってほしいです。

―この問題解決のまとめはp.184～185 で行うことになります。この場面はどのように指導されますか。

小岩　ここは1時間とって授業をしたいですね。❷では「箱ひげ図を分析してわかること」を、❸では「❷でわかったことをもとにどう判断するか」を聞いています。この２つを棲み分けしたいと考えています。

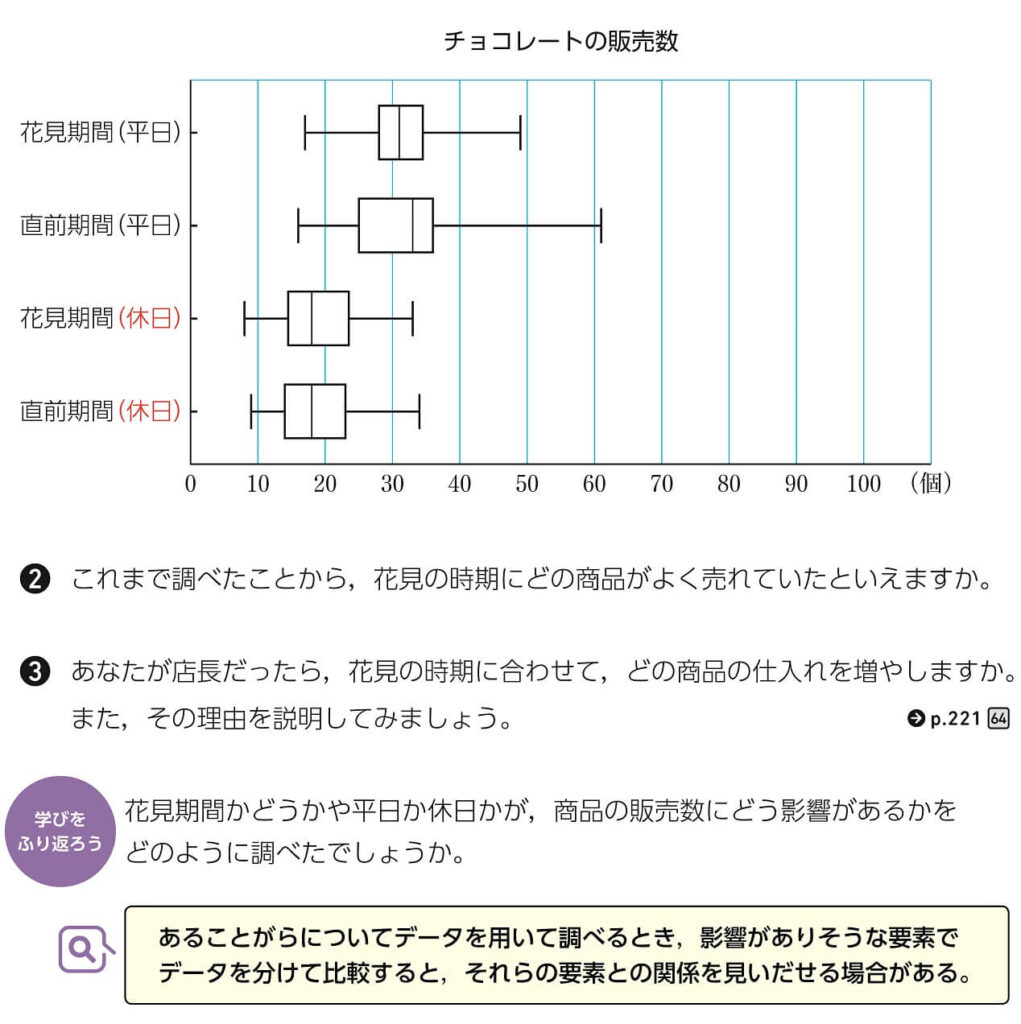
佐藤　「❷はPPDAC のプロセスでいうとAnalysis（分析）ですね。分析したうえで、❸でConclusion（結論）を導き出すということです。「スナック菓子の販売数は、花見期間の休日の箱が右に位置している」という分析は、比較的表現できると思います。これをもとに「～ということは～します」と結論づけることの方が難しいかもしれません。

小岩　「箱ひげ図を読み取って考えてみよう」と発問すると、図を分析して分かることと、分かったことから判断した結論が混在すると思います。まずは分析したことを共有し、それから分析したことをもとに結論づけるというように分けたほうがよいと考えています。

佐藤　箱ひげ図の単元の振り返りでは、箱ひげ図を使って考えることのよさを考えさせたいですね。先生は箱ひげ図で分析を進める際のメリットとデメリットについてはどうお考えですか。

小岩　箱ひげ図は、複数のデータの傾向を同時に見ることができるメリットがあります。一方で、ヒストグラムでは見えていた山の形が見えなくなるため、細かいデータの傾向を調べられない点がデメリットだと考えています。箱ひげ図のよさと同時に、限界も学ぶ必要があります。

佐藤　この単元は、義務教育で学ぶ記述統計の最後の単元ですので、記述統計全体を振り返ってほしい。小学校では棒グラフや折れ線グラフなどの使い分けをしています。中学校でも、ヒストグラム、箱ひげ図など、どのように使い分けていけばよいかをまとめて、学んだ統計手法を、目的に応じて自ら選択できるようになってほしいと考えています。

＊＊＊　ここからWEB限定記事です　＊＊＊

散らばりの表し方の小中高の連携

―今回の指導要領の改訂で、四分位数や箱ひげ図は高等学校から中学校に移行しました。また、代表値は小学校で取り扱うようになりました。小中高の連携についてはどのようにお考えですか。

 佐藤　データを分析するときには「散らばりぐあい」をみることが重要だと考えています。小学校ではドットプロットを学び、データの散らばりぐあいを考えています。それをより視覚化したものが箱ひげ図です。中央値も小学校で扱うので、ドットプロットで散らばりぐあいをみる傾向が強くなると考えていますして作られているんですか。

 佐藤　小中の繋がりを意識したとき、小学校で散らばりぐあいをどう捉えてきたのかを知った上で、中学校で散らばりぐあいをどうみて問題解決できるか考えたいです。ドットプロットでは、ドットが上に重なるために、高さがあるから複数の比較が難しいですね。その点で、箱ひげ図はすっきりと表されています。そういうことを指導したいですね。

 小岩　そうですね。散らばりぐあいをみることについては繋がりを意識して指導したい。ドットプロットもヒストグラムも分布をみる道具ですが、箱ひげ図は分布を見るのに特化している。これが、高校になると分散に繋がります。中学校では中央値を基準に散らばりぐあいを考えますが、高等学校では平均値を基準に散らばりぐあいを捉えることになります。

 佐藤　大学生に標準偏差の話をすると、計算演習は多かったがそれを用いた統計的な問題解決をしたことは覚えていないと話していました。今、小岩先生が指摘した見方の話をすると感心していました。大学生たちは学びが途中でとぎれているように思えます。そうならないように関連を意識したいですね。

対談を振り返って

子どもが主役の学びをデザインするときには、次のことを大切にしたいと思いました。

〇箱ひげ図の導入場面では、データをまとめた複数の分布の様子について、一度に比較したいという必要感をもたせられるようにする。

〇実際に生データに触れさせ、それを見るといった活動も大切にして、分析の計画（Plan）へと繋げる。

〇単元全体を通したPPDACサイクルの実現と義務教育における統計の内容をまとめることで、統計的に問題解決することのよさやヒストグラムや箱ひげ図などの統計手法の必要性を確認する。

Profile

佐藤　寿仁 　Toshihito Sato
岩手県公立中学校で11 年、岩手大学教育学部附属中学校で6 年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。

小岩　大 　Dai Koiwa
愛知県公立中学校で4年、東京学芸大学附属竹早中学校で10年以上教職を務める（現職）。生徒が数学をつくるプロセスを重視した授業づくりに力を注ぎ、各地で飛び込み授業や講演などを行っている。

この記事は2022年1月に発行した「がんばる先生のための算数・数学情報誌math connect Vol.3」をもとに作成しています。