特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【math connect】トークセッション:子供…

「主体的・対話的で深い学び」を実現するために、教科書をどう読み解き、授業づくりに活用していけばよいのでしょうか。
今回は、第1学年「待ち時間の予想はできるかな?」を取り上げ、お二人の先生に、教科書を活用した学びのデザインについて、「日常場面の問題発見・解決」「数学化」をキーワードにお話いただきます。


数学を使って解決しようとする姿勢を大切にする
―この題材は、前回の教科書では単元の導入でしたが、今回は利用の節の導入です。扱い方も変わるのでしょうか。
小岩 利用の節の導入なので、子どもは比例について一通り学んできています。これまでよりも比例が前面に出てくるでしょう。比例定数や式を使って解決することが予想されます。
佐藤 授業を考える際には、問題発見・解決の過程(図1)をより意識して考える必要があると思うのですが、いかがでしょうか。

小岩 数学の問題をつくり出す過程(図1のA1)を大切にしたいですよね。現実の場面で数学を使えるようにするには、厳密には比例でないものを比例であると仮定することが必要です。それを子どもが考えていくことが、授業の中心になると思います。
佐藤 小学校では、必要な画用紙の枚数を数えずに求めるといった問題(図2)があります。画用紙の問題には比例関係が内在していることがわかりますが、行列の問題は厳密には比例とはいえないものを比例とみなして考える必要があります。小学校と中学校の取り扱いの違いも意識しておきたいところです。

小岩 これまでは、もともと比例関係がある事象で比例を使うのが中心でした。これからは、厳密には比例でないものも比例とみなして、積極的に数学を使って解決しようとする姿勢が大事だと思います。行列の問題の解決を通して、そういうことを教えたいですよね。
佐藤 以前実践したとき、行列の問題を解決したあとに、小学校の教科書(画用紙の問題)を子どもに見せたことがあります。「何が変わったと思う?」と問うと、「小学校のときは、はっきりしてたものをやってた」「中学校ではそうじゃなくても比例を使えるようになった」といった反応がありました。校種を超えて振り返ることで、子どもが算数数学の学びにお ける成長を実感できることも大事だと思います。
数学化するプロセスを子どもと一緒にたどる
―この問題を扱うとき、50分の授業の中で軽重をつける必要があると思います。どこが授業の「山場」になるのでしょうか。
小岩 一番の山場は、問題場面を整理するところだと思います。厳密には比例でないものを比例とみなして、比例関係の特徴を使って解決していくために、条件をどのように整理すればよいかを、子どもが考えるところです。
佐藤 教科書では「長い行列ができています」という事象との出会いから始まります(図3)。そして「ショーが始まるまでに・・・」というはるかさんのセリフがありますね。このあたりを、先生はどのように扱いますか。

小岩 子どもをはるかさんの立場に立たせます。「今、遊園地に来ています。ショーが始まるまでに時間があるからどうする?」「おなかがすいた。遊園地といえば何を買う?」のように状況把握をしてから、行列のイラストを見せます。「ポップコーンを買うのにこんなに並んでいます。ショーに間に合うだろうか」として、Q の問題を提示します。
佐藤 「ショーが始まるまでに間に合うかな」のセリフがとてもよいと思います。与えられた問題ではなく、子どもが「どうなるのかな」「間に合うのかな」と考えてみたくなる。こういうセリフを子どもとどう共有できるかが大切だと思います。待ち時間を予想するときは、どのように発問しますか。
小岩 教科書の❶のように「待ち時間を予想したいのだけど、どのようなことがわかればよいか」と発問します。これがこの授業で一番大事な発問になると思います。
佐藤 そうですよね。問題解決の構想を立てる場面で、先生には自信をもってこのことを発問してほしいと思います。「何がわかればよいか」という発問に対する子どもの反応はどうですか。また、ここからどのように授業を進めていきますか。
小岩 「一人が買うのにかかる時間」と「並んでいる人数」という意見が必ず出てくることが予想されます。子どもは比例を使えると思って発言します。つまり、二つの数量に比例関係があることを疑っていません。ここで問い返す必要がありますが、いつ問い返すかのタイミングが難しいです。
佐藤 先生はどのタイミングで問い返すのですか?
小岩 非常に悩みます。自力解決前に子どもに聞いて、行列の進み方を一定とみなしていることを確認してから解決に入るパターンと、そこをおさえずに自力解決に入って、あとで解決を振り返って一定と考えていたことを確認するパターンがあると思います。
小岩 私が所属校でない学校で行った授業では、自力解決の前に聞いても子どもが反応できない可能性があると考えて、自力解決のあとで確認しました。解決の発表の中で「一人あたり・・・」という考えが出たことを振り返って、「行列の進み方をどのようにみているの?」と問い、「一定とみている」「比例とみなしている」という数学の言葉につなげて展開しました。
佐藤 私が以前実践したときは、初めに「一人が買うのにかかる時間」を一定とみてよいかどうか検討することを問いました。子どもは「並んでいる誰か一人が買うのにかかる時間がわかればいいよ」と言いました。そこで「そのようにみてもいいのかな?」と発問することで初めて、子どもが疑問に思い、「一人一人買うのにかかる時間は違う」ということに気づきます。つづけて、「一人一人買うのにかかる時間は違うけど、この問題を解決するにはどう考えたらいいかな?」と聞くと、「その時間は一人一人そんなには違わないんじゃないかな」と考える子どもも出てきて、話し合いが進んでいきます。
小岩 問題解決するために比例とみなすことは、あくまで問題解決するための「仮定」であることを認識することも大切だと思います。「実際に一人が買うのにかかる時間は同じか」については、「この問題では5分間で8人進んだということしかわかっていないけれど、例えば実際に一人一人にかかった時間を調べればよい」といった発想がもてるとよいですよね(図4)。

佐藤 板書には「比例とみなして考えると…」など、「仮定」であることをはっきりと示しておきたいところです。板書に示すことで、あとで振り返ることができます。先生のお話を聞いて、解決したあとに振り返らせて、数学化するプロセスを評価するという発想も大事だと感じました。
*** ここからWEB限定記事です ***
-問題解決を振り返る場面では、どのようなことがポイントになりますか。
小岩 振り返る場面では「この問題を解決したときに、どんな考えが大切でしたか?」と問います。自力解決する前に、この行列では一人が買う時間を一定として考えることを確認したならば、それを取り上げます。確認しなかったならば、「この問題を解決できたのは、行列の進み方をどのように考えていたからですか」などと問います。
佐藤 問題解決で使った数学やその見方・考え方を整理して、それを生徒が価値付けていくということですね。そのあとは、どうされますか?
小岩 「この行列について、一人が買うのにかかる時間を一定と考え、比例とみなして解決した」という意見が出ると予想されるので、「実際には本当に一定なのかな?」と問い返します。
佐藤 その問い返しは大事ですよね。逆に「一定とみることができないような状況ってあるかな?」と聞いてもよいと思います。そうすると生徒は、イラストを見て「ここにはポップコーンだけを売っている」ということに気づきます。「焼きそばとかいろいろなものが売っていたら、買うものも増えるからお店の人も大変。今はメニューがポップコーンだけだから手間がかからず、一人が買うのにかかる時間も一定として考えていいのではないか」のような話が出てきます。一見数学の話ではないが、比例とみなしてよいかどうかにつながるので掘り下げてみたいと考えます。
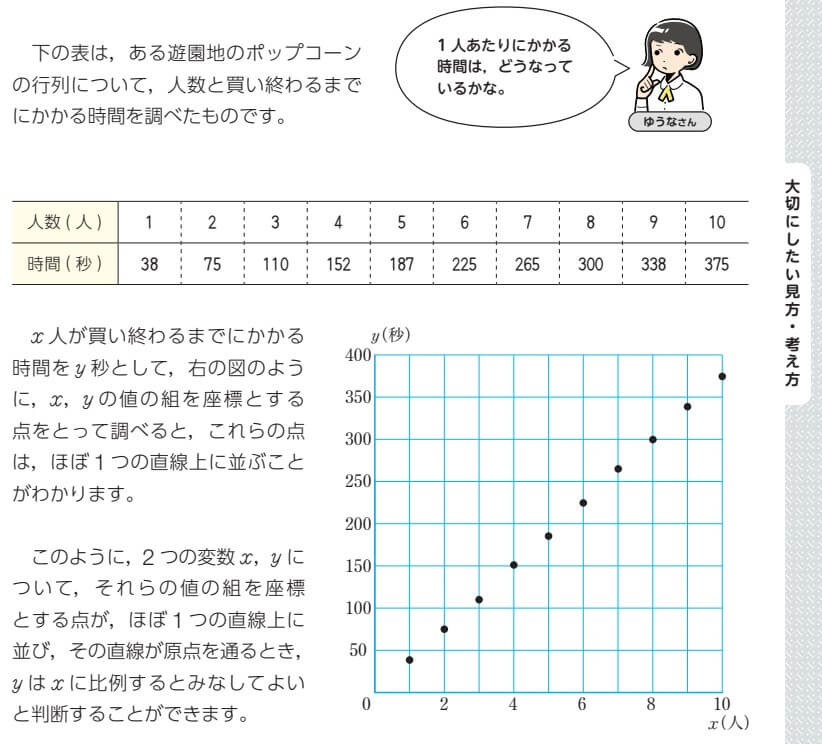
小岩 今回は利用の節で扱っているので、できれば比例とみなしていい根拠もきちんと問いたいところです。実際に1人ずつにかかる時間を調べて(図5)、どのように変化しているかを考察して、比例とみなしてよいことを判断できるようにしたいですよね。
佐藤 同感です。解決したあとで事象に戻って、さらに数理的に吟味するところまで考えて授業ができるとよいですね。
小岩 さらに、振り返る際に大切だと感じているのは「身の回りで比例を使って先のことを予測できるものを探してみよう」と生徒に問うことです(図6)。学習評価が知識・技能であれば練習問題に取り組むのと同じように、問題解決をする際に比例とみなして考えることを学んだならば、その目で日常の事象を見て活用することができないかどうかを考えることが大切です。生徒からは不動産に出てくるような「徒歩○分」とか「スーパーの量り売りのお肉の代金」、テレビ番組などで出てくる「カップラーメン1年分」(笑)なども出てきました。比例の目で身の回りの事象をみる、そのような経験が大切だと思っています。

佐藤 子どもにとっては、算数から数学になって、日常からどんどん遠ざかってしまうような感覚があります。そういう意でも、このような身の回りの題材を扱うことはとてもよい数学の学びとなりますね。この題材を通して、数学の楽しさや未来を予測できるという数学のすごさを体験的に知ることができればよいと考えます。こういったことが、私たちが関数を指導することの意義の一つだと思います。
対談を振り返って
子どもが主役の学びをデザインするときには、次のことを大切にしたいと思いました。
◯「厳密には比例ではないが,二つの数量の間にある関係を比例とみなして考える」といった問題解決するために関数関係を仮定して考える場面を授業に取り入れる。
◯問題解決の過程を振り返る場面を設定し,「比例とみなして考えたこと」を取り上げ,理想化したり単純化したりして考えたことを確認する。
◯働かせた数学的な見方・考え方をもとにして,他の事象でも同じようにみることができなかどうかを考察することを促す。このことで,生徒の数学的な見方・考え方は豊かになっていくと考えられる。
Profile
佐藤 寿仁 Toshihito Sato
岩手県公立中学校で11 年、岩手大学教育学部附属中学校で6 年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。
小岩 大 Dai Koiwa
愛知県公立中学校で4年、東京学芸大学附属竹早中学校で10年以上教職を務める(現職)。生徒が数学をつくるプロセスを重視した授業づくりに力を注ぎ、各地で飛び込み授業や講演などを行っている。
その他のコンテンツ
