特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【思考を見せる板書例】3年3章:2次方程式\(x^…
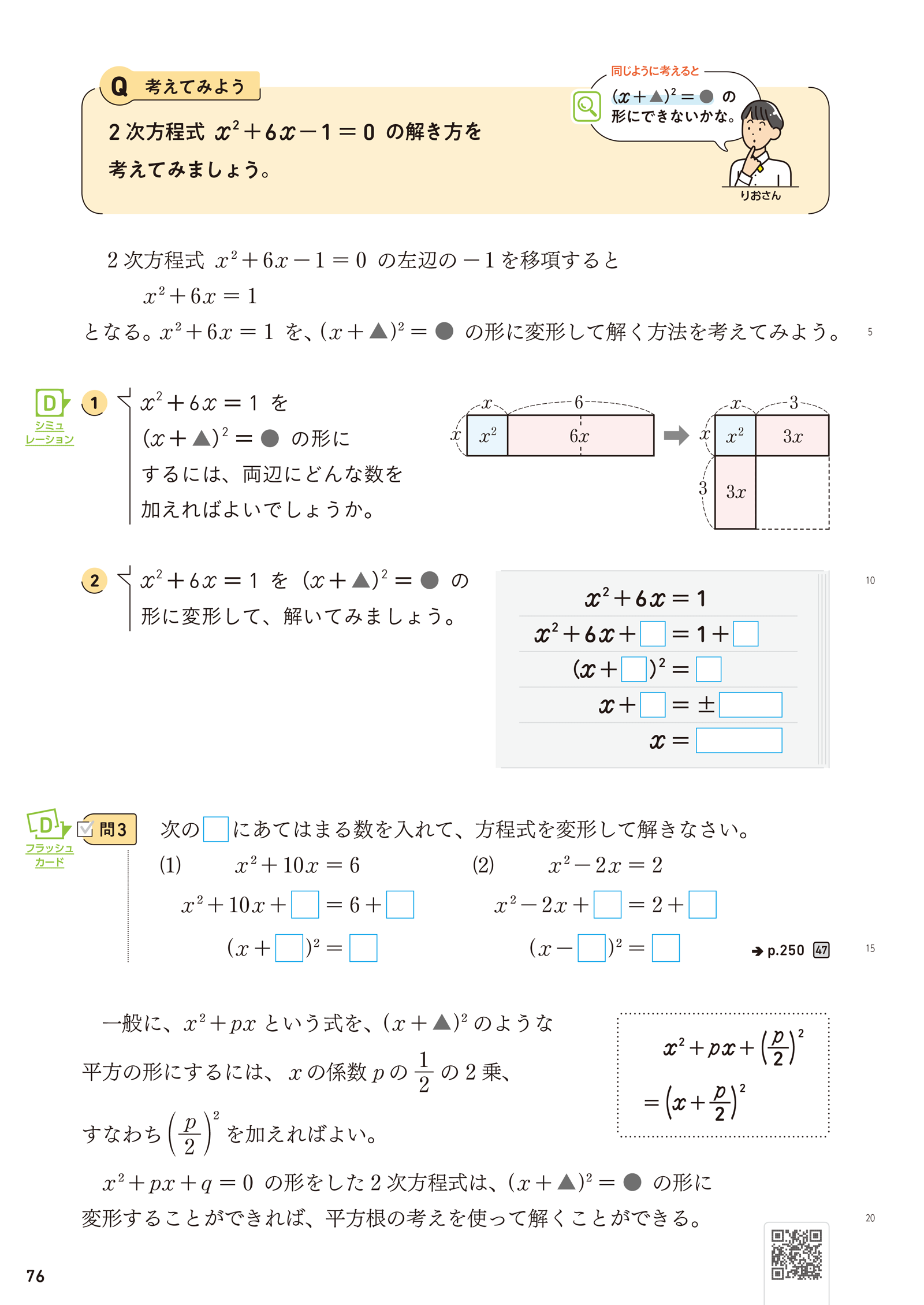
教科書紙面はこちら
今回紹介する板書例は、「新編 新しい数学3」p.76「2次方程式 \(x^2+6x-1=0\)の解き方について考えよう」です。前時までに、\(ax^2+c=0\)や \((x+▲)^2=●\) の形をした2次方程式を、平方根の考えを使って解くことを学習しています。ここでは、2次方程式 \(x^2+px+q=0\)の形をした2次方程式を、既習の内容である \((x+▲)^2=●\) の形に変形して解くための方法について学習していきます。

ポイント
- これまでに解いた2次方程式の形を振り返り、「\((x+▲)^2=●\)の形になったら解ける」という考え方を取り上げて、既習事項との関連を意識させる。
- 面積図や公式などの既習内容をもとにして、式変形の考え方をていねいに取り上げ、考えが進むように促す。
- 未知の形の2次方程式を既習の形に変形することで解くことができていることを確認する。
- 計算演習では、計算の過程が分かるように丁寧に記述し、技能の定着をはかる。
板書の執筆 筑波大学附属中学校 近藤俊男先生
※所属は執筆時
その他のコンテンツ