特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

不確定な事象を考察すること 〜データの活用：確率〜 ②

Q　データの活用の領域では、1、2年生のどちらにも確率の内容が設定されているのですが、1年生ではどのような授業が求められているのでしょうか。

Ａ　不確定な事象を考察する場面を設定し、事柄の起こりやすさを調べることのよさを感得できるような授業づくりが大切です。

　前回は領域「データの活用」の「確率」の指導の意義について、みなさんと考えました。今回は、1年生の学習内容について指導の意義を確認し、授業づくりのポイントを確認しましょう。

□事柄の起こりやすさを調べること

　前回も確認しましたが、中学校学習指導要領（平成29年告示）解説数学編では「データの活用」での指導の意義について説明されています。大切なことですので、もう一度確認します。

　確率を正しく計算することはもちろん大切ですが、求めた確率の値を起こりやすさの程度として捉え、不確定な事象について考察し、それを説明することも大切です。現行の学習指導要領では確率の学習を第1学年と第2学年に分けています。前学習指導要領では確率は2年生でした、こちらのほうがしっくりくるという先生もいらっしゃるのではないでしょうか。このことについての是非を考えるのではなく、両学年における確率について、その目標である知識及び技能の資質・能力をみてみましょう。

　確率というと「場合の数を基にして得られる確率」を想起すると思いますが、「多数の観察や多数回の試行に着目した確率」もあります。1年生におけるデータの活用では、相対度数とその求め方を知ることになります。相対度数は、全体（度数の合計）に対する部分（各階級の度数）の割合を示す値であることを学習しますが、計算して求めることだけでなく、各階級の頻度とみなして考えることができることの理解も必要です。さらに、それらの学習と1年生での確率の学習をつなげることが大切です。

□事柄の起こりやすさを確率をもとに説明する活動

　実際に1年生の確率の授業づくりについて考えます。1年生では「多数の観察や多数回の試行によって得られる確率」の指導です。

　これは、「新しい数学1」の7章3節「ことがらの起こりやすさ」の冒頭にあるものです。ホエールウオッチングをしたいと考えるはるかさんが、ツアーを企画しているA社とB社のどちらに申し込むか悩んでいるところです。「クジラを見たい、でも、必ずしもクジラに出会うことができるかどうかはわからない、さて、どうしよう…」という場面把握を生徒と一緒に進め、A社とB社を選択するときの“決め手”となることについて考えます。ホエールウオッチングですから、第1の目的はクジラを見ることです。「どのようにして判断すればよいか？」と生徒に問うと、「よりクジラに会うことができる会社を選ぶ」と答えるでしょう。そのためにはどんなこと（データ）が必要かを問い、確認してから下のようなデータを提示するとよいです。

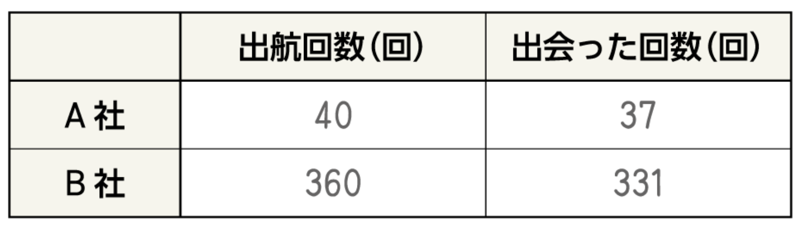
クジラに出会った回数についてのデータ

　このデータをもとに、生徒が話し合うことで、出会った回数はB社が多いものの、A、B社の出航回数が異なることに着目すると、単に出会った回数が多いからといってB社のほうがよいとは限らないことに気付くのではないでしょうか。最初は出会った回数だけを提示することもよいかもしれません。そして、どうすれば判断できるのかと問いかけ、下のように「（出会った回数）\(\div\)（出航回数）」を計算し、表に書き加えるとよいでしょう。

クジラに出会った回数についてのデータを用いて算出

　計算された値を生徒は「割合」と考えて、それらの値の大小関係に着目してどちらの会社を選択するか説明し合うことが期待されます。
　生徒の説明を評価する際には、単にどちらを選んだかだけでなく、0.925と0.919の大小関係を捉え、「A社のほうがB社よりも値が大きいから、より出会いやすいといえる」のように根拠を示しているかどうかを確認しましょう。生徒によっては「出会う確率が92.5％と91.9％だから」のように、百分率を用いて説明する生徒も予想されます。中には、「0.925と0.919の大きさに差があまりないから、どちらでもよい」という説明も予想されます。
　不確定な事象の起こりやすさの傾向として数値化するといった表現を通して、「必ず〜になる」とは言い切れない事柄について、数を用いて考察したり判断したりすることができることを知り、数学と日常生活や社会との関係を実感できるようにすることが大切です。

※参考資料

• 新しい数学1（東京書籍）
• 中学校学習指導要領（平成29年告示）解説数学編

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。