特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

令和6年度全国学力・学習状況調査の結果を生かした授業づくり⑥

Q　令和6年度全国学力・学習状況調査問題の大問９の問題の設問（２）を用いた授業づくりのポイントを教えてください。

Ａ　大問９の設問（２）を用いた授業づくりについて、問題解決する場面を「予想−行動−振り返り」の「行動」と「振り返り」という視点で考えることができます。

　前回は、令和6年度全国学力・学習状況調査問題の中でも正答率が低かった大問９（２）の問題を用いた授業づくりについて取り上げました。今回は、「予想する-行動する-振り返る」の「行動する」と「振り返る」について取り上げ、問題解決の場面づくりを考えてみましょう。

□生徒が実際に「行動する」場面での教師が寄り添うこと

　前回は、大問９設問（２）において、コンピュータなどを利用して図を動的にみて観察することで、成り立つことを予想することについて取り上げました。ここでは、図の\(\triangle \text{AQC}\)と\(\triangle \text{BPC}\)の大きさの関係についての着目を促し、“変わるもの”と“変わらないもの”という視点で図３を観察することを通して、２つの角についていえることを話し合い、成り立つ事柄を予想することが大切です。

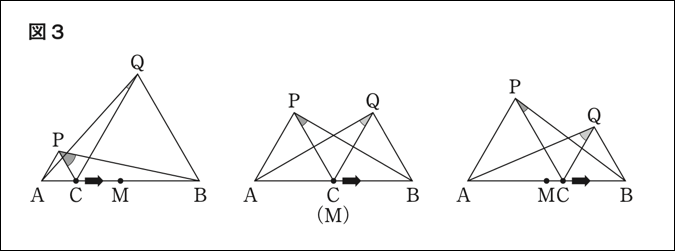
令和6年度全国学力・学習状況調査問題大問９（２）の図

　しかしながら、図３の\(\angle \text{AQC}\)と\(\angle \text{BPC}\)の「和」に注目すること自体、生徒にとってあまリ経験のないことです。よって、まず\(\angle \text{AQC}\)から点Cの動きによって大きさがどのように変わるのか、同様に、\(\angle \text{BPC}\)についてもその大きさについて考えた後、調査問題のように\(\angle \text{AQC}\)と\(\angle \text{BPC}\)の「和」に焦点化するとよいです。しかし、これを明らかにすることは容易ではありません。調査結果をみても、下の①に\(60^{ \circ }\)があてはまることを正しく指摘できたのは、全体のうち45.1％です。また、①、②のどちらもウを選択した反応率は27.4％でした。この設問は選択式の問題ですので、解答の根拠は読み取ることができません。

令和6年度全国学力・学習状況調査問題大問９（２）の問題と選択肢

　調査結果から、この（2）についての解答状況は大変厳しいことがわかりました。では、実際の授業では、このことをどのようにして生徒が問題解決に向かうことがよいのでしょうか。これを「行動する」という局面で考えてみましょう。
　まず、図における\(\text{AQ=PB}\)を示した（1）の証明をもとに振り返ります。\(\text{AQ=PB}\)を示すために、どのような数学的事実と向き合ったのでしょうか。それは、\(\triangle \text{QAC}\)と\(\triangle \text{BPC}\)が合同であるという関係です。この関係が\(\text{AQ=PB}\)を成り立たせるものになっていますから、証明を読んで、下のような発問が考えられます。

　このように問いかけることで、証明を読み、\(\triangle \text{QAC}\)と\(\triangle \text{BPC}\)が合同であることから2つの三角形の構成要素間の相等関係などについて、下のように捉えることが予想されます。

　わかったこと㋐〜㋒を踏まえ、\(\angle \text{AQC}=\angle \text{PBC}=x\)、\(\angle \text{QAC}=\angle \text{BPC}=y\)と表したことで、下の図のように\(x+y=60^{ \circ }\)になること、さらに\(\angle \text{AQC}+\angle \text{BPC}=x+y=60^{ \circ }\)から2つの角\(\angle \text{AQC}\)と\(\angle \text{BPC}\)の和は\(60^{ \circ }\)になるといえることに気づくでしょう。

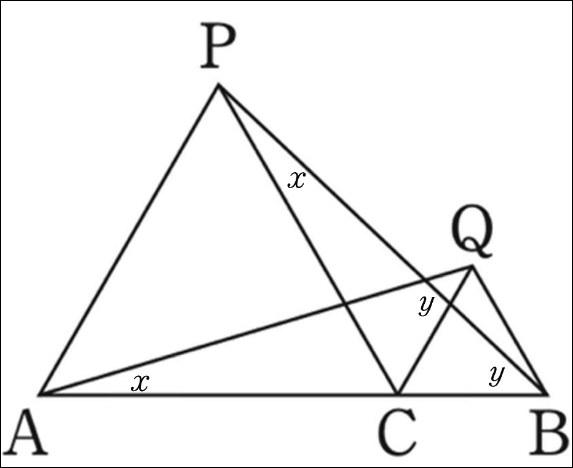
　このように説明することについて、生徒は経験していないことも考えられます。よって、多少は教師が先導することもあるでしょう。このようなときには、わかっていることを生徒が捉え、それを数学的に表現することや数学的表現を解釈し関係を見いだすことができるよう、教師の発問を工夫して生徒の出番をつくりましょう。教師は、生徒と共に歩む姿勢を見せ、生徒に行動を促すことが大切なのです。

　さて、こうした「行動する」ことで問題解決を終えた後、「振り返る」場面を設定しましょう。その際、単なる感想ではなく、「難しいと感じたところはどんなことだったのか」「それをどのように乗り越えたのか」「新しく知った数学の見方や表現方法は何か」のような視点を紹介し、問題解決での数学の自らの行為を振り返ることを促しましょう。

※参考資料　

• 令和6年度全国学力・学習状況調査解説資料中学校数学（国立教育政策研究所）
• 令和6年度全国学力・学習状況調査報告書中学校数学（国立教育政策研究所）

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。