
北野天満宮
はるかです。お正月は、みんなで合格祈願! 北野天満宮に、初詣にやってきました。
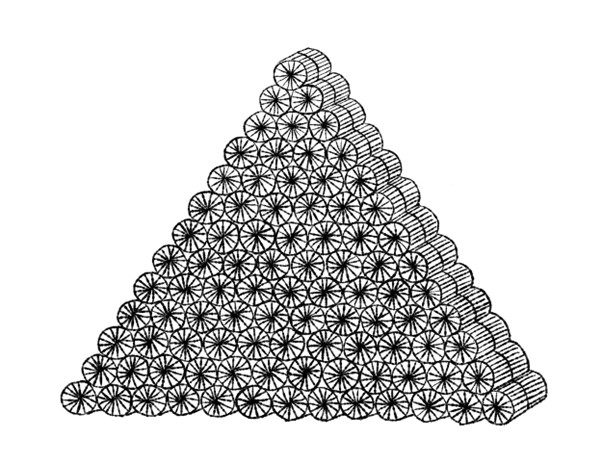
へえぇ、これが「絵馬所」。ずいぶん古そうな、立派な絵馬がたくさんあるね。あっ、これは少し新しそう。なんだか不思議な絵だよ。図形かな。

ひろとさん、いいところに気づいてくれた! これは「算額」といって、数学の問題を絵馬に書いて、奉納したものなんだ。この算額は明治時代に奉納されたそうだよ。
ちなみに、江戸時代に日本で独自に発達した数学を「和算」というんだけど、「和算」といわれるようになったのは明治時代からなんだって!
和算といえば、小学校で「つるかめ算」や「入れ子算」をやったな。中学でも、米俵を積み重ねる問題が出てきたよ。
でも、どうして神社に奉納したんだろう?
よく覚えているね、そうたさん。難しい問題が解けたことを神仏に感謝して、奉納されるようになったと言われているよ。苦労した問題が解けたときって、うれしいでしょ?
うん、確かに、うれしい! この算額の問題って、どんな問題なの?
そうそう、ゆうなさん。それを見てみなくちゃね。左から2番目の問題は、こうだよ。「二等辺三角形の内部に4つの円が互いに接していて、三角形の上斜(等辺)が1014寸、下斜(底辺)が1428寸のとき、甲円の直径を求めよ」

うわぁ、どこから考えればいいかな。まず、1寸は3センチくらいだったっけ……?
ルーロー、これはさすがに難しすぎるよ。
ハハハハ、さすがはるかさん。じゃあ、もう少し簡単にして考えようか。円、三角形、四角形を組み合わせて……こんな問題はどう?
問題:1辺10cmの正方形と、底辺が正方形の上辺と重なり、頂点が正方形の下辺上にある二等辺三角形がある。その二等辺三角形の内部に接している円の半径を求めよ。
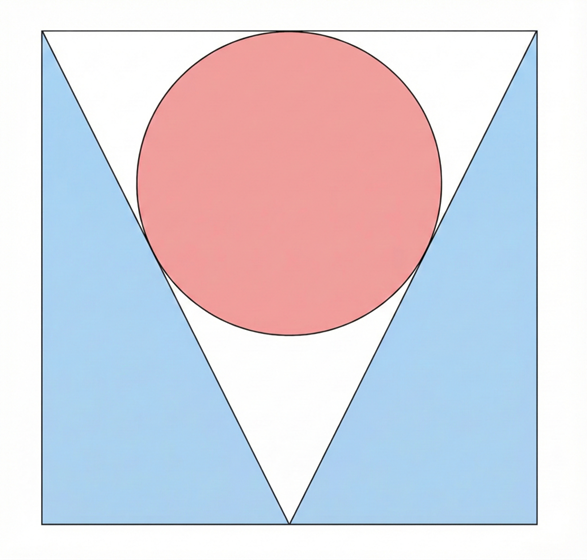
作図しちゃえば簡単だよ。図形やグラフが作れるツール「GeoGebra」は、どうかな? 問題文をていねいに読みながら、やってみるよ……
まず、1辺が10cm の正方形。次の二等辺三角形は、底辺が上で頂点が下だから、さかさまだね。ここにピッタリになるように円をかいて測ってみると……うん、半径は3.1cmだ。
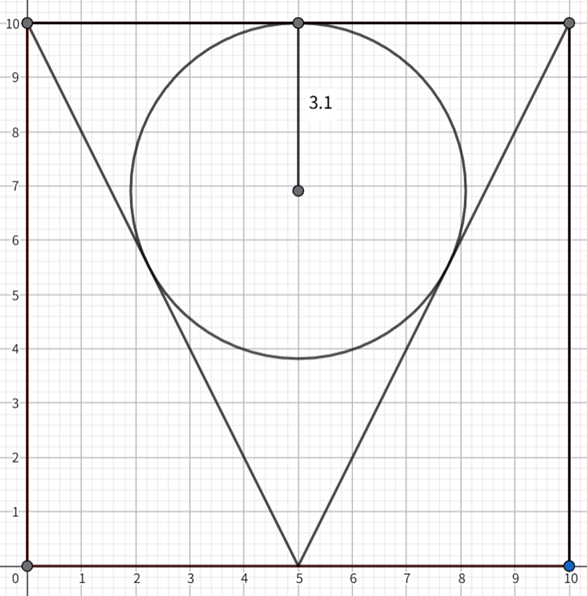
なるほど! GeoGebraは便利だね。ひろとさん、使いこなしてるなぁ。
ぼくは計算で求めたいな。「円外の1点から、その円に引いた2つの接線の長さは等しい」という性質や三平方の定理を使って、いろいろなところの長さを調べると……こんな風になるよ!
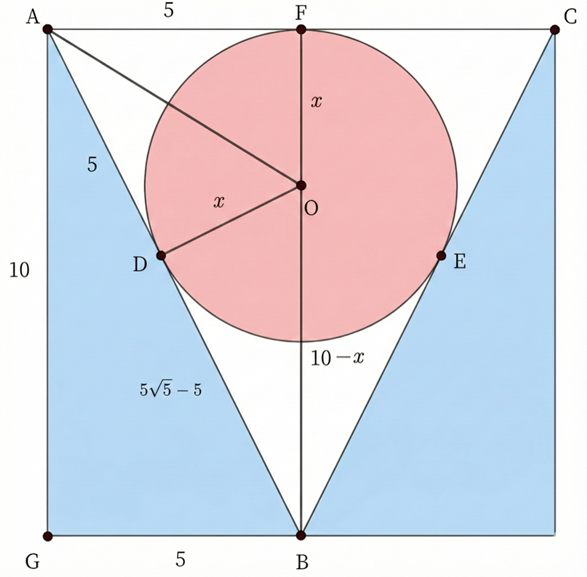
ふむふむ。図の中の\(x\)が円の半径、つまり求めたい数だよね。
\(\triangle \text{BOD}\)の3辺がわかったから、三平方の定理を使って方程式をつくるよ。
\(x^2+(5\sqrt{5}-5)^2=(10-x)^2\)
これを解くと
\(x=\cfrac{5\sqrt{5}-5}{2}\)(cm) だ!
そうたさん、すごいな。三角形に着目したんだね。今の話を聞いて、面積の考え方も使えそうだと思ったよ。大きい二等辺三角形の面積は、中にある3 つの三角形の和だよね。しかもこの3 つの三角形、高さが共通だから……。

ゆうなさんも、やるね! さらに簡単に解けそうだ。他にも、いろいろな考え方があるよ。例えば、座標を使うとか。そうたさんの図から、相似な三角形を見つけるとか。三角形の、こんな性質を使うとか。

よーし、私はその性質を使ってやってみる。お正月から、なんだか勢いがついちゃうね。全国のみんなも、受験、がんばりましょう〜!
*北野天満宮/京都府京都市。菅原道真をまつる、全国約1万2千社の天満宮・天神社の総本社。入試合格、学業成就、文化芸能、厄除けのお社として広く信仰されている。
*写真提供:北野天満宮
*イラスト作成:大野寛武
〒602-8386 京都府京都市上京区
その他のコンテンツ
