
本栖湖
夏休み!
ますりん、あみさんと一緒に、富士山の近くにやって来ました。湖に映る富士山、きれいだなぁ。お札の裏面に、こういう絵がなかったっけ?
さすが、こうたさん。2024年まで発行されていた野口英世の千円札の裏面が、まさにここ、本栖湖から見た「逆さ富士」だったよね。もちろん、「逆さ富士」が見られるのは本栖湖だけじゃないよ。富士五湖の全部の湖に、富士山がちゃんと映って見えるんだ。
富士五湖というのは、富士山の周りにある5つの湖だね。山中湖、河口湖、西湖、精進湖……。
そう。それに、ここ本栖湖を加えて5つ。
あみさん、やるなぁ。
なかでも一番大きいのは、どの湖かな。富士山のてっぺんから見れば、すぐにわかるね。登ろうか!
もちろん登ってみたい! でも頂上から5つの湖までの距離は、それぞれ違うよね? 近くの湖は、大きく見えそう。大きさを比べるなら、湖の周りの長さがいいんじゃないかな。
こうたさんの考え方、いいね。自分の目で比べてみる。でも確かにあみさんが言う通り、今回は見え方だけで大きさを決めることはできないかもしれない。ちなみに、それぞれの湖の1周の長さは
河口湖 約20.9km
山中湖 約13.9km
本栖湖 約11.6km
西湖 約9.9km
精進湖 約6.8km
だよ。
いちばん長いのは、河口湖だね。
待って、全部が同じ形なら1周の長さで大きさを比べてもいいけど、湖はそれぞれ形が違うでしょう。こういう場合を考えてみて?
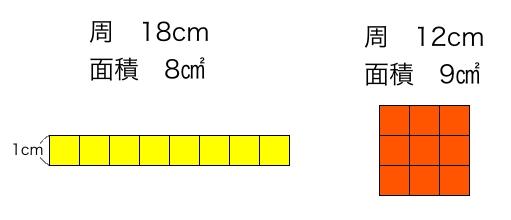
なるほど、形が違うときは、周の長さが長いほど面積が大きくなるわけではないんだね。困ったな。あ、地図を見てみる?
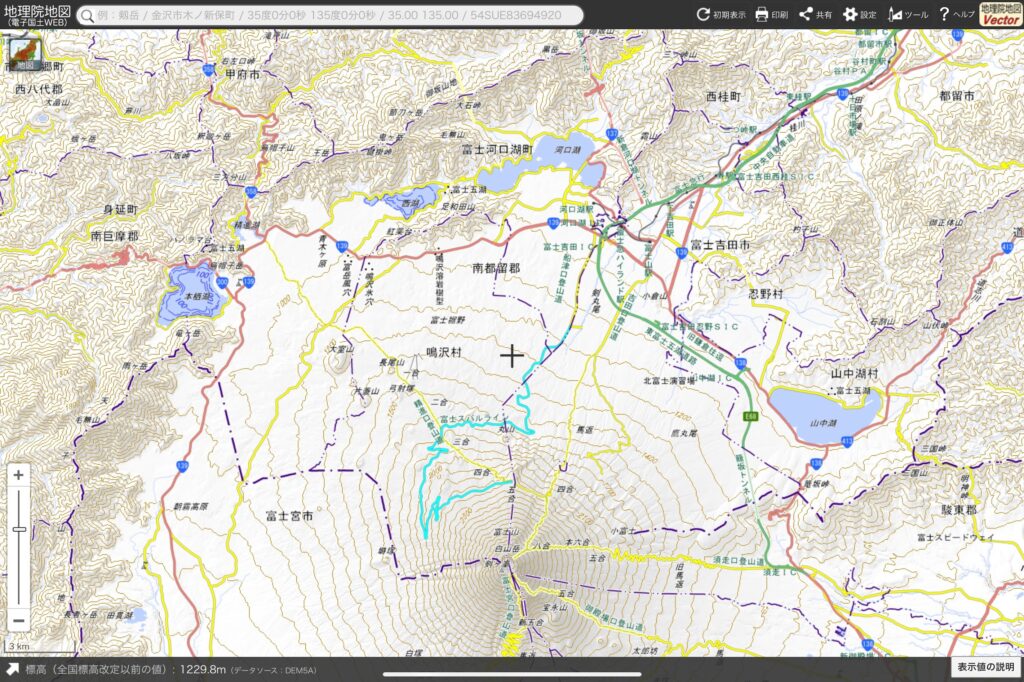
*出典:国土地理院webサイト
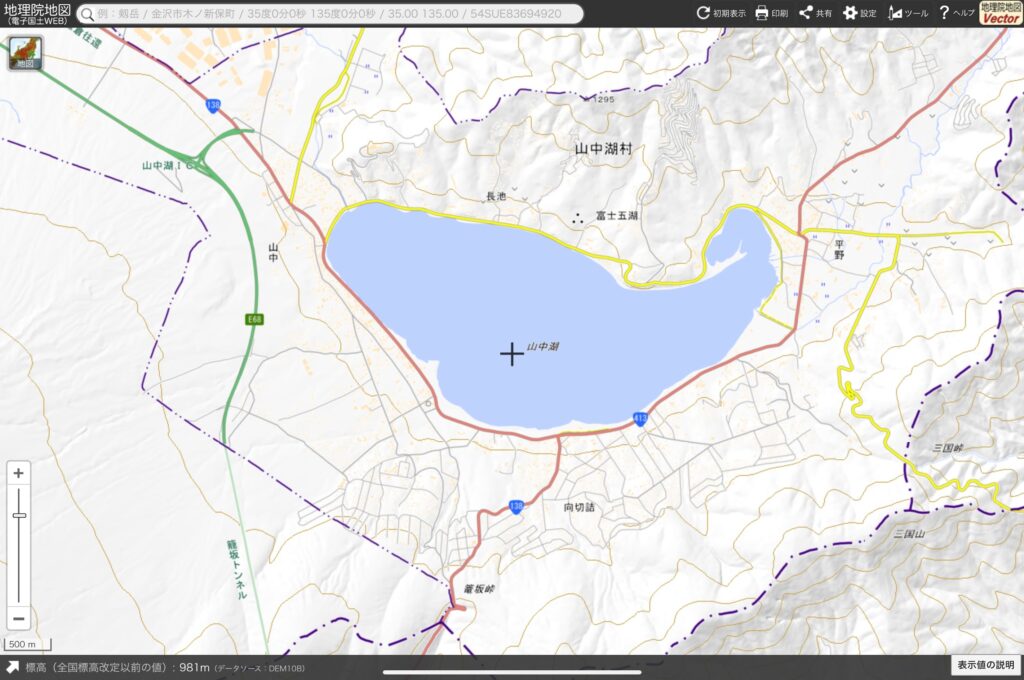
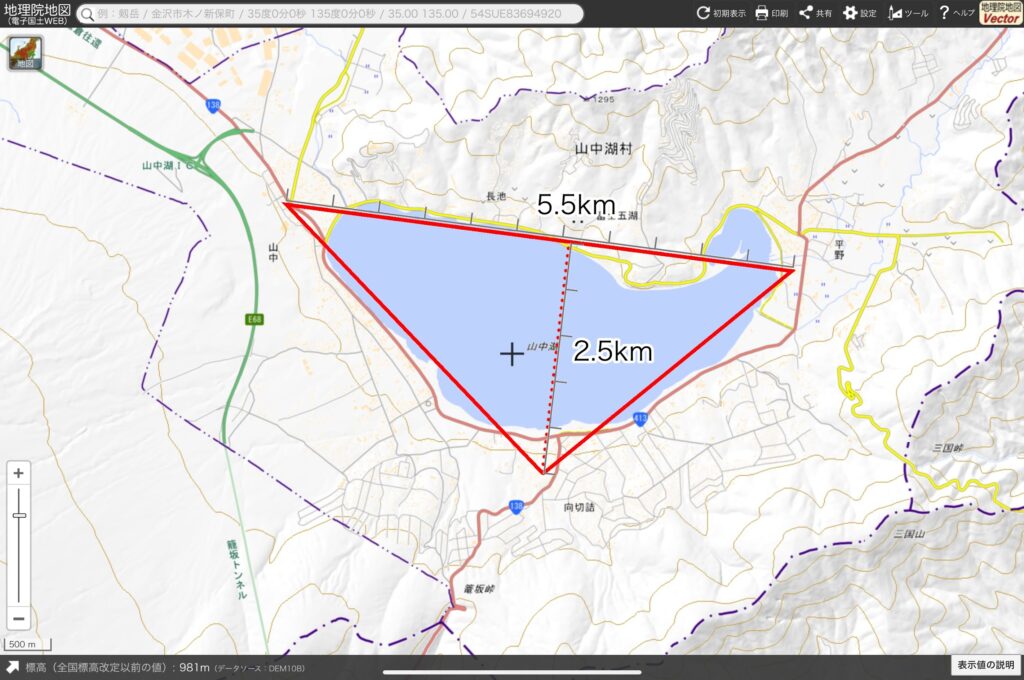
そうか、まず地図を見るべきだった。山中湖と河口湖が大きそうだけど、どちらが大きいかな。微妙だな。たとえば山中湖は三角形っぽいし本栖湖は台形っぽいから、この2つなら、だいたい計算できそうなんだけどな。まず山中湖は、こんな三角形で考えればいいよ。
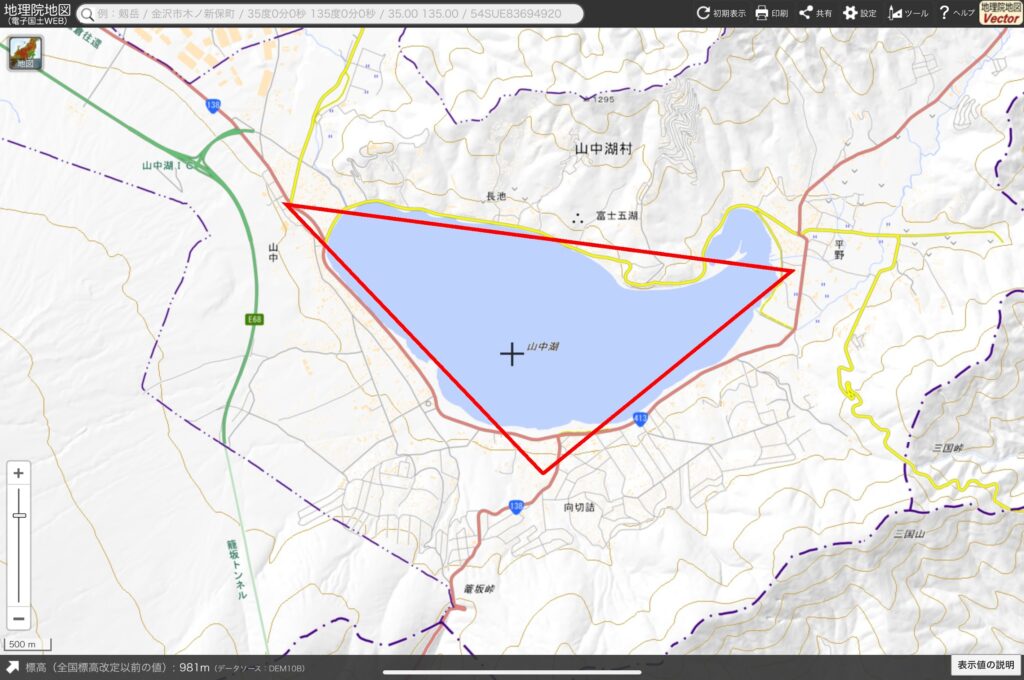
*出典:国土地理院webサイト(東京書籍で赤線を加筆)
「500m」の尺度があるから、これを元にしてものさしで測るよ。この三角形の底辺は約5.5km、高さは約2.5kmだ。だいたいの面積は
\(5.5 × 2.5 ÷ 2 = 6.875\) 約\(6.9\)㎢
になるってこと。
*出典:国土地理院webサイト(東京書籍で赤線を加筆)
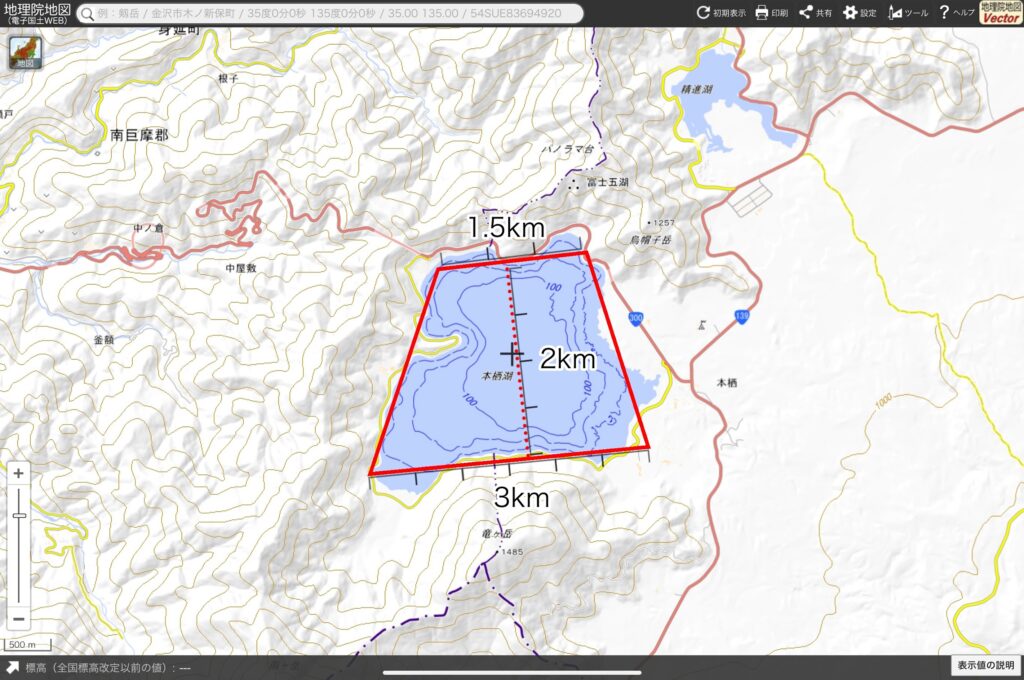
わぁ、スッキリするね! じゃあ私は、本栖湖を考えてみる。この台形の上底は約1.5km、下底は約3km、高さは約2km。だいたいの面積は
\(\text{(}1.5+3\text{)}× 2 ÷ 2 \text{=} 4.5\) 約\(4.5\)㎢
になったよ。
*出典:国土地理院webサイト(東京書籍で赤線を加筆)
2人とも、バッチリ! 河口湖はどうしようか?
うーん。直線で囲んでみたけど、形がちょっと複雑すぎるよ。
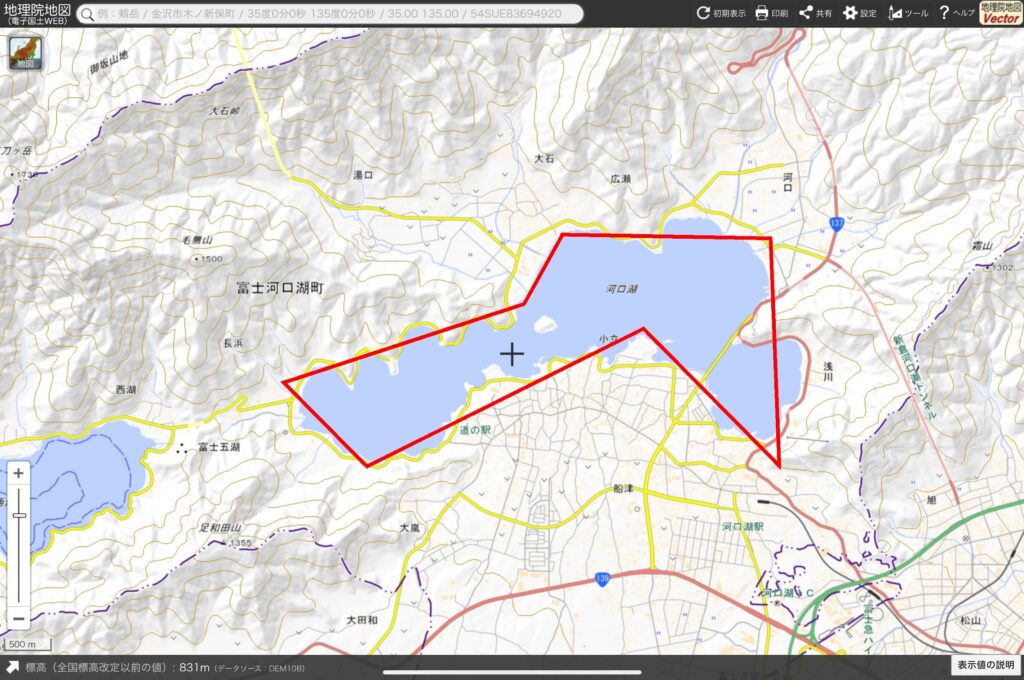
*出典:国土地理院webサイト(東京書籍で赤線を加筆)
待って、三角形なら計算できるんだから……こんなふうに、切り分けたらどう?
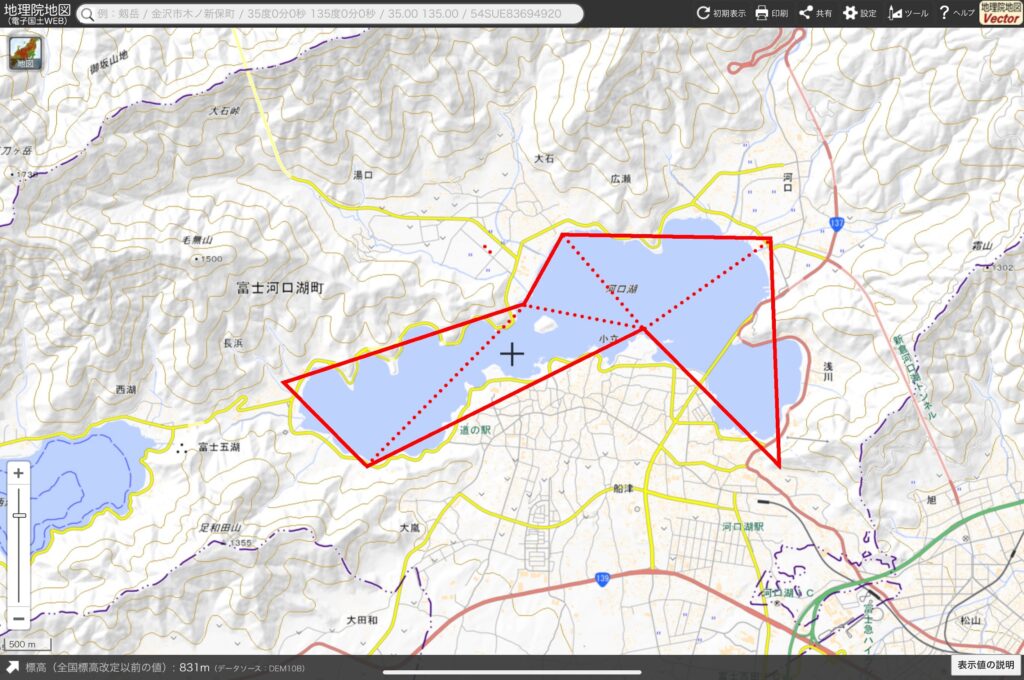
*出典:国土地理院webサイト(東京書籍で赤線を加筆)
あみさん、ナイスアイデア! これは実際に使われている方法で、「三斜法」という名前もあるんだよ。どんなに複雑な形の土地でも、三角形に切り分ければ、それぞれの三角形の底辺と高さから面積を求めることができるんだ。
複雑に見えたけど、三角形に分けると、たった5つなんだね。前に琵琶湖の水の量を計算したときに比べたら、ラクラクだ。
よーし、手分けして計算していこう!
*富士五湖/山梨県。富士山の北の麓にある5つの湖が、まとめてこう呼ばれている。東から順に山中湖(山中湖村)、河口湖(富士河口湖町)、西湖(富士河口湖町)、精進湖(富士河口湖町)、本栖湖(富士河口湖町、身延町)。
*イラスト作成:大野寛武
山梨県
その他のコンテンツ
