
2025年日本国際博覧会(大阪・関西万博)・大屋根リング
はるかです。今日は、みんなそろって大阪の夢洲(ゆめしま)にやってきました!
「EXPO2025大阪・関西万博」の会場だよね!楽しみだったんだ〜。
あれが大屋根リングだね。こうやって見ると、本当に大きいな。
そりゃ、ひろとさん、なんといっても「世界最大」だよ。ギネスにも認定されたし。
さすがそうたさん、くわしいね。認定の理由は建築面積、つまり上から見た面積が「世界最大の木造建築」だから。
会場全体をひとつの建築で囲むなんて、びっくりのアイディアだよ。確かに全部が木でできていて、たくさんの柱が十字にクロスしてるね。「清水の舞台」の下の方って、こんな感じじゃなかったっけ……?


おっ。ゆうなさん、よく気づいたね。柱に開けた穴に「貫(ぬき)」と呼ばれる横向きの材木を通して、「楔(くさび)」で固定して作っているんだ。まさに清水寺などで使われている、伝統的な技法なんだよ。
しかもこのリングをぐるりと一周すると、ちょうど2025mらしいよ。「EXPO2025」つながり?
さらに、それが偶然だというから驚くね。大屋根リングの幅は、30m。ギネスの認定を受けるにあたって真ん中の15m地点で実際に測ってみたら、2025mだったんだって。
建築面積は、そこからもすぐにわかりそう。外周の半径を\(a\)(m)、内周の半径を\(b\)(m)とすれば
\({\pi}a^2-{\pi}b^2\)で計算できるよ。
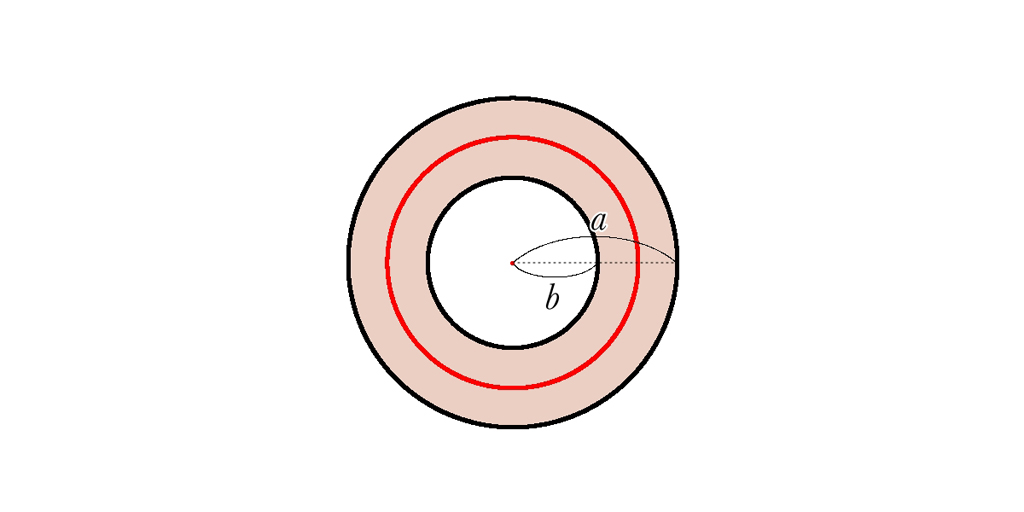
よーし! じゃあ、まずは外周と内周の半径から求めようか。15m地点の円周が2025mだから
\(2{\pi}\)\({r}\text{=}2025\)
\({r}\text{=}2025\text{÷}2\text{÷}3.14\)
\( \ \ \text{=}322.45\)(m)
外周の半径は\(322.45\text{+}15\text{=}337.45\)(m)で、
内周の半径は\(322.45\text{−}15\text{=}307.45\)(m) ということだね。すると、求める面積は
\({\pi}\text{×}337.45^2-{\pi}\text{×}307.45^2\)
\( \ \ \text{=}357559.66\text{−}296810.08\)
\( \ \ \text{=}60749.58\)
60749.58㎡ だ!
ひろとさん、目の付けどころがいいね。 ギネス記録は61035.55㎡ となっているから、そうたさんの計算もバッチリ、ほぼ正解だ。ちなみにこのリングは正確にいうと円ではなくて、直線状のユニットを109個つないだ109角形なんだよ。
そんな計算をしなくても、リングの幅が30mで周の長さが2025mの道だから
\(30×2025=60750\) 60750㎡
でいいんじゃない?
だって、道が曲がってるんだよ? 簡単にいくわけがないよ。
ね、ちょっと待って。円の面積の求め方みたいに考えてみたら? ええと、まずリングを4等分して互い違いにくっつけてみると、こうでしょ?
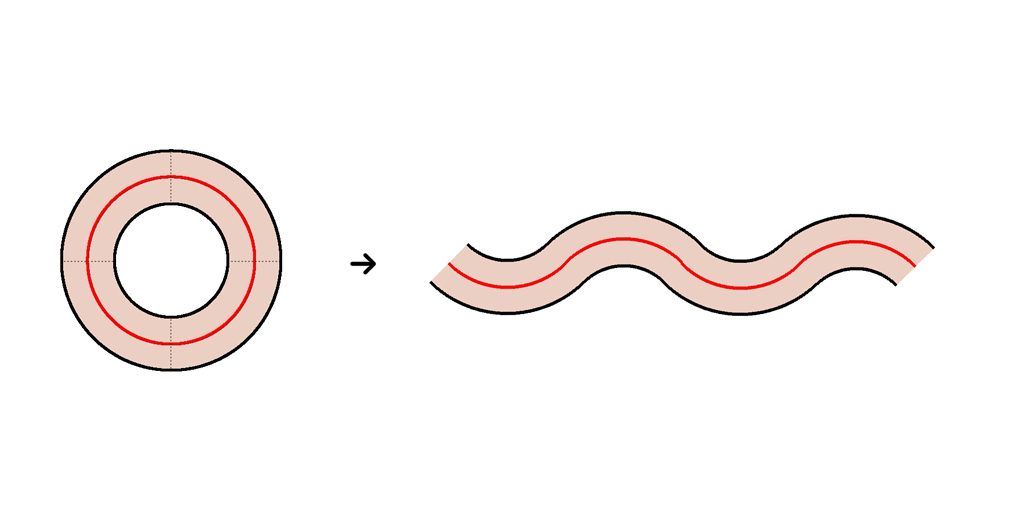
12等分すると、こう。
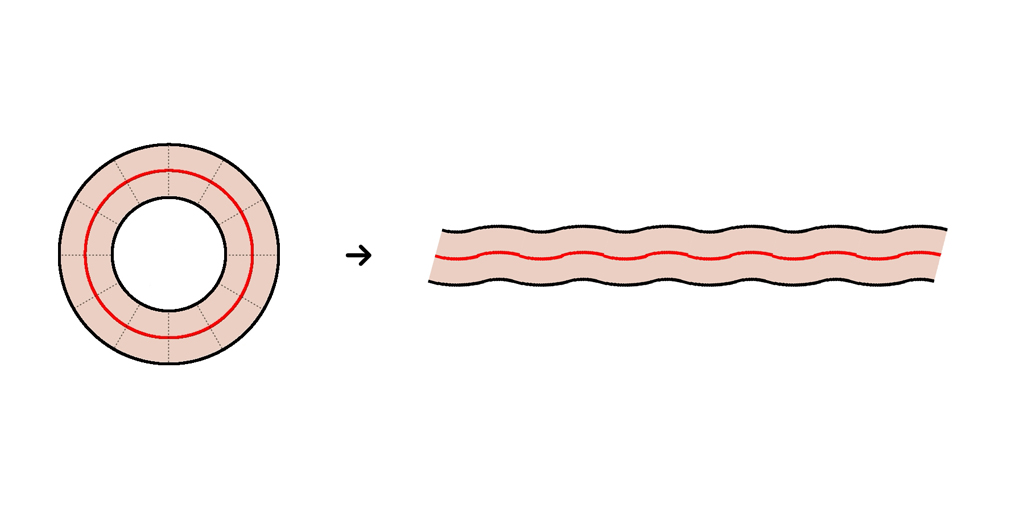
もっと細かく24等分すると、こう。だんだん、直線みたいになっていくよ。
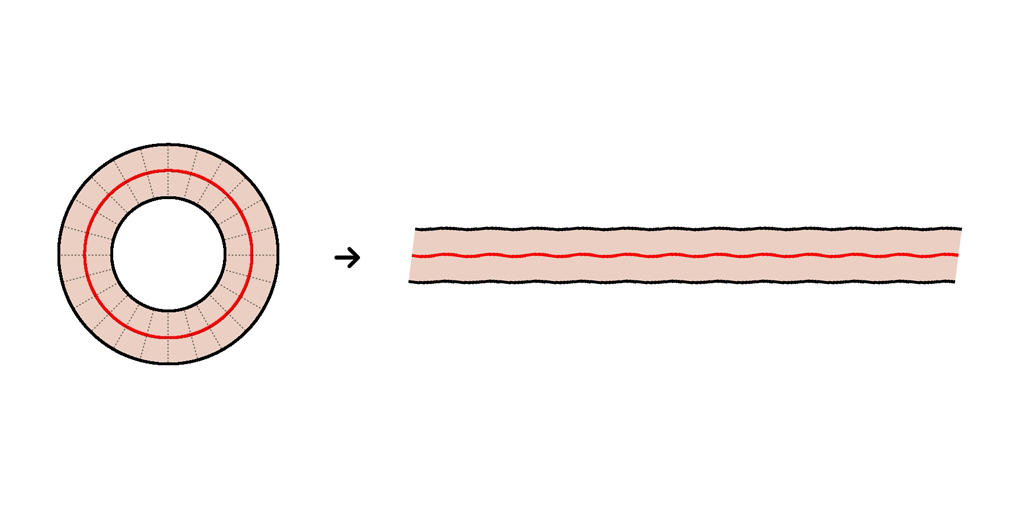
なるほど!「道幅×周の長さ(\(30×2025\))」に説得力が出てきたね。
文字式でも説明できるかも。さっき考えた
「\({\pi}\)\(a^2-{\pi}\)\(b^2\)」の式に、因数分解を使うんだ。
\( \ {\pi}\)\(a^2-{\pi}\)\(b^2\)
\(={\pi}\)(\(a^2-b^2\text{)}\)
ここで、「平方の差」の因数分解の公式が使えるから
\( \ {\pi}\)(\(a^2-b^2\text{)}\)
\(={\pi}\)(\(a+b\))(\(a-b\))
リングの真ん中15m地点の半径を\(r\)とすると外周の半径\(a\)、内周の半径\(b\)はそれぞれ
\(a=r+15\)
\(b=r-15\)
だから
\( \ {\pi}\)(\(a+b\))(\(a-b\))
\(\begin{eqnarray}={\pi}\lbrace\text{(}r+15\text{)}+\text{(}r-15\text{)}\rbrace \\ \lbrace\text{(}r+15\text{)}-\text{(}r-15\text{)}\rbrace\end{eqnarray}\)
\(={\pi}×2r×30\)
ええと、ここまでは来たけど……。
\(2{\pi}\)\({r}\)って、円周だよね。円周は2025m!
つまり「リングの面積=\(30×2025\)」だ!



*2025年日本国際博覧会・大屋根リング/大阪府大阪市此花区。大阪・関西万博会場デザインプロデューサーである建築家の藤本壮介氏が構想。高さ約12mのスカイウォークが会場の主な動線となると同時に、地上には雨風・日差しが遮られた快適な空間を作る。
写真提供:2025年日本国際博覧会協会
写真提供・イラスト作成:大野寛武
〒554-0043 大阪府大阪市此花区
その他のコンテンツ
